1. What have we achieved?

Variable types

• numeric
• categorical

What we have achieved:

• Confidence intervals (numeric variable)
• t-tests, Mann–Whitney (means of numeric variable by one categorical variable with two levels)
• χ², Fisher test (categorical by categorical)
• Simple linear regression (numeric by one numeric variable)
• ANOVA (means of numeric variable by categorical any variable)
• Multiple linear regression (numeric by several numeric variables)
• Multiple linear regression with dummy variables (numeric by any variable)

Today:

• Logistic (logit) regression (binary dependent variable by any number variables of any type)

2.1 How it works

Logistic or logit regression was developed in [Cox 1958]. It is a regression model wich predicts binary dependent variable using any number of variables of any type.

What do we need?

\[\underbrace{y_i}_{[-\infty, +\infty]}=\underbrace{\mbox{β}_0+\mbox{β}_1\cdot x_1+\mbox{β}_2\cdot x_2 + \dots +\mbox{β}_k\cdot x_k +\mbox{ε}_i}_{[-\infty, +\infty]}\]

But in our case \(y\) is a binary variable.

• Probability?

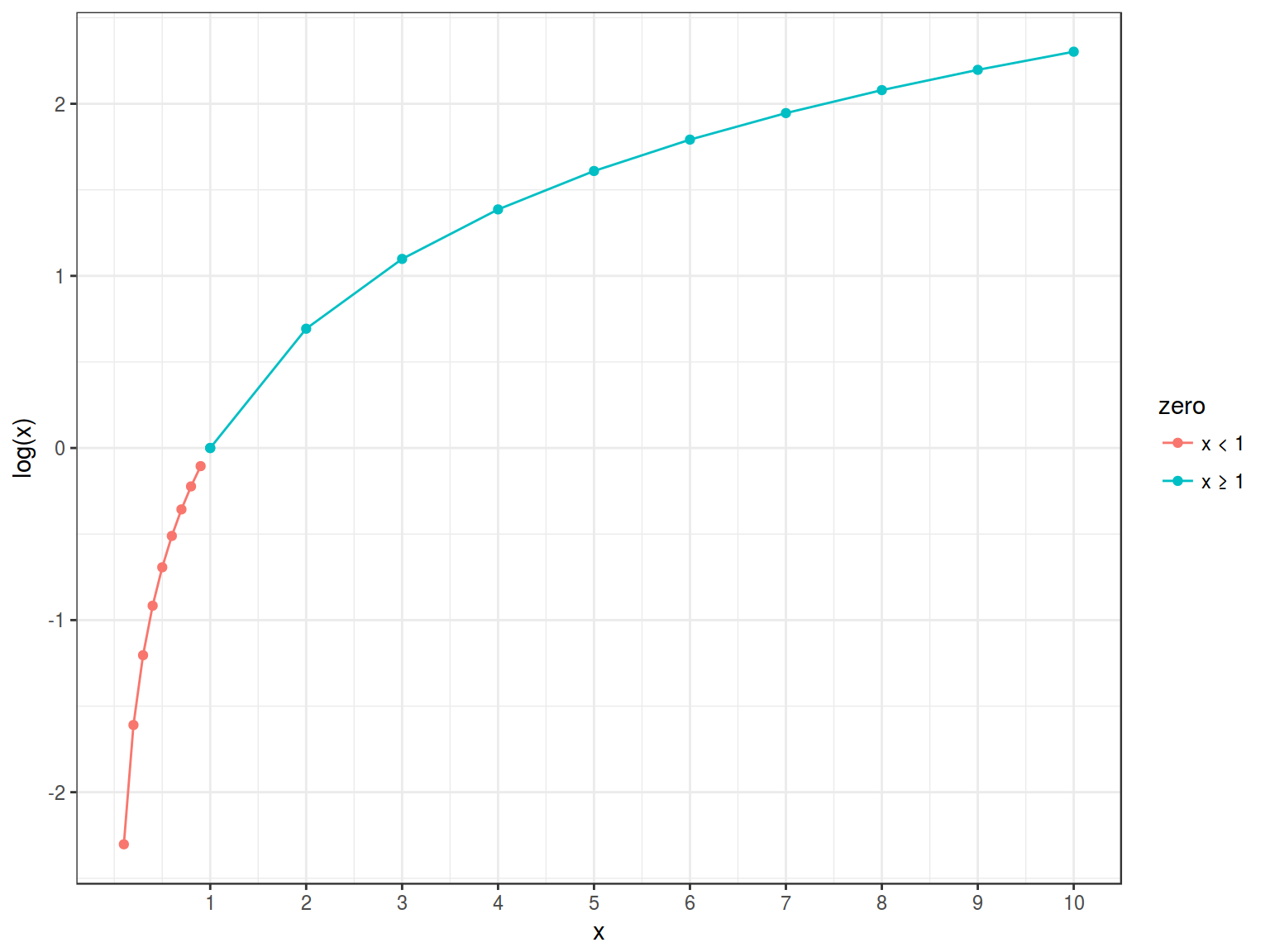
\[P(y) = \frac{\mbox{# successes}}{\mbox{# failures} + \mbox{# successes}}; P(y) \in [0, 1]\]

• Odds?

\[odds(y) = \frac{P(y)}{1-P(y)} = \frac{\mbox{P(successes)}}{\mbox{P(failures)}} = \frac{\mbox{# successes}}{\mbox{# failures}}; odds(y) \in [0, +\infty]\]

• Natural logarithm of odds

\[\log(odds(y)) \in [-\infty, +\infty]\]

2.2 Reminder about logarithms

• if log(odds) are greater then 0, it means that we have more successes then failures;
• if log(odds) is equal to 0, it means that we have the same number of successes and failures;
• if log(odds) are less then 0, it means that we have less successes then failures;

2.3 probability ←→ log(odds)

\[\log(odds(s)) = \log\left(\frac{\#s}{\#f}\right)\] \[P(s) = \frac{\exp(\log(odds(s)))}{1+\exp(\log(odds(s)))}\]

Results of the logistic regression can be easily converted to probabilities.

2.4 Sigmoid

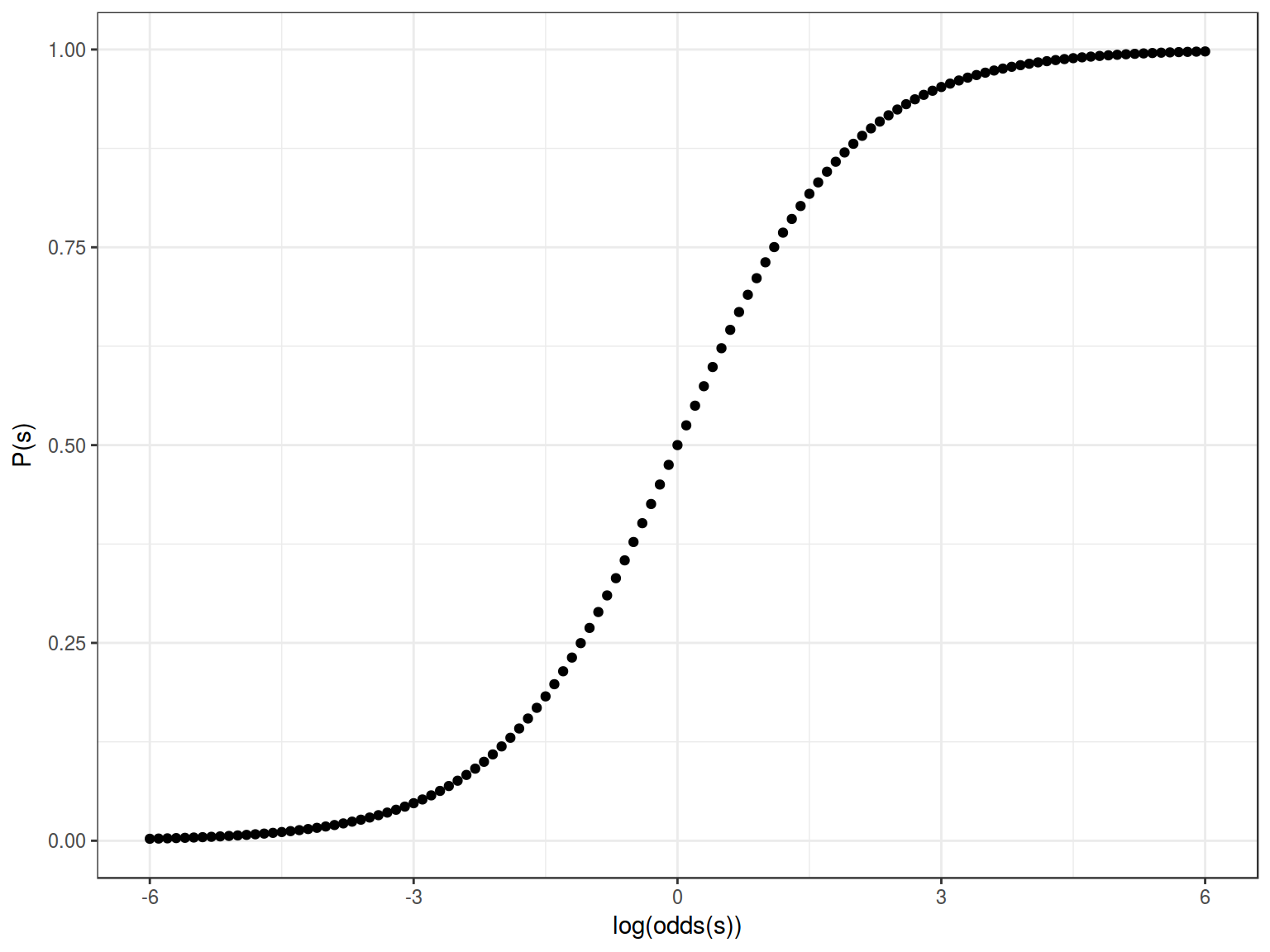
Formula for this sigmoid is the following:

\[y = \frac{1}{1+e^{-x}}\]

Feeting our logistic regression we should be able to reverse our sigmoid:

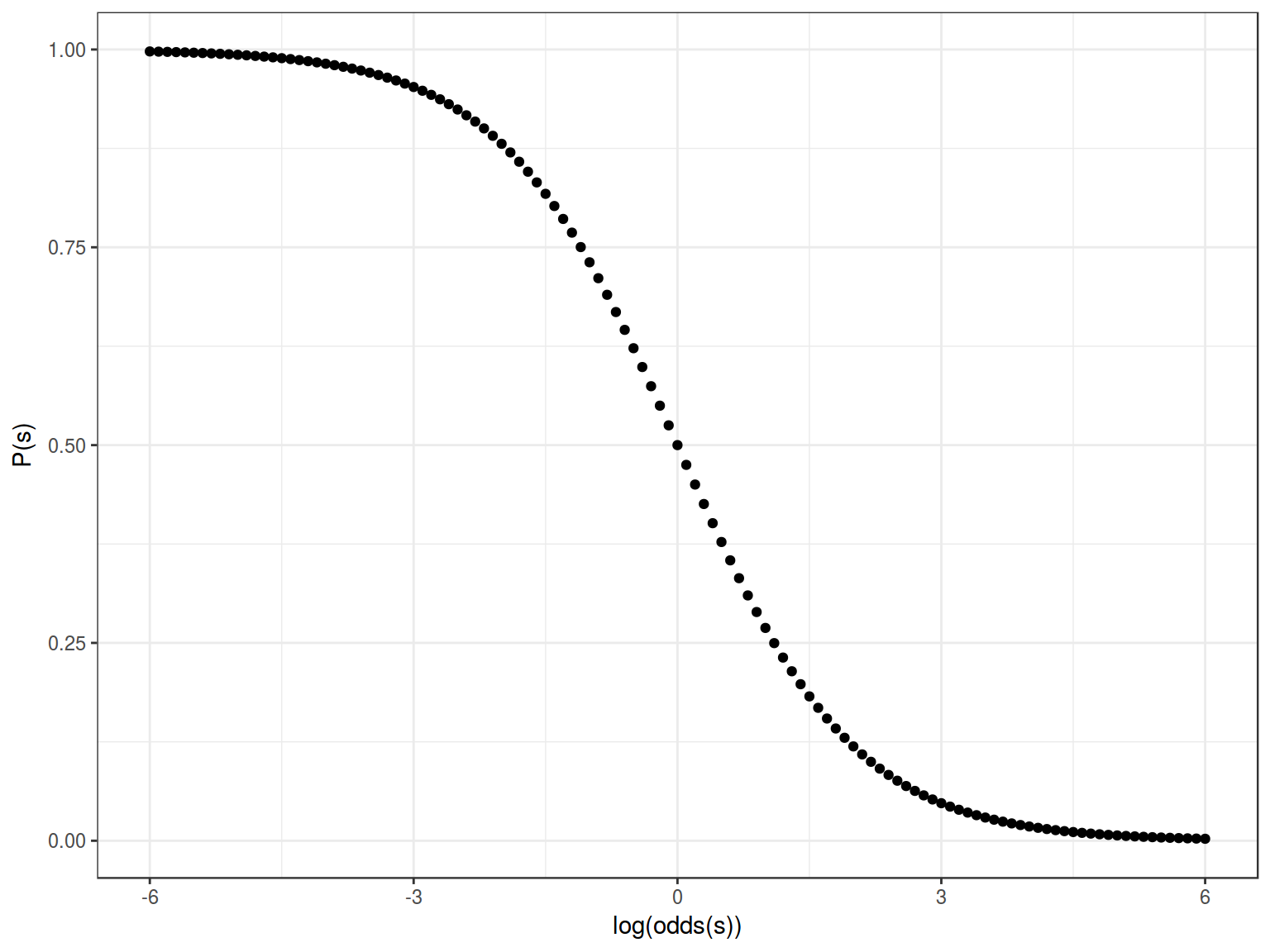
Formula for this sigmoid is the following:

\[y = \frac{1}{1+e^{-(-x)}} = \frac{1}{1+e^{x}}\]

Feeting our logistic regression we should be able to move center of our sigmoid to the left/right side:

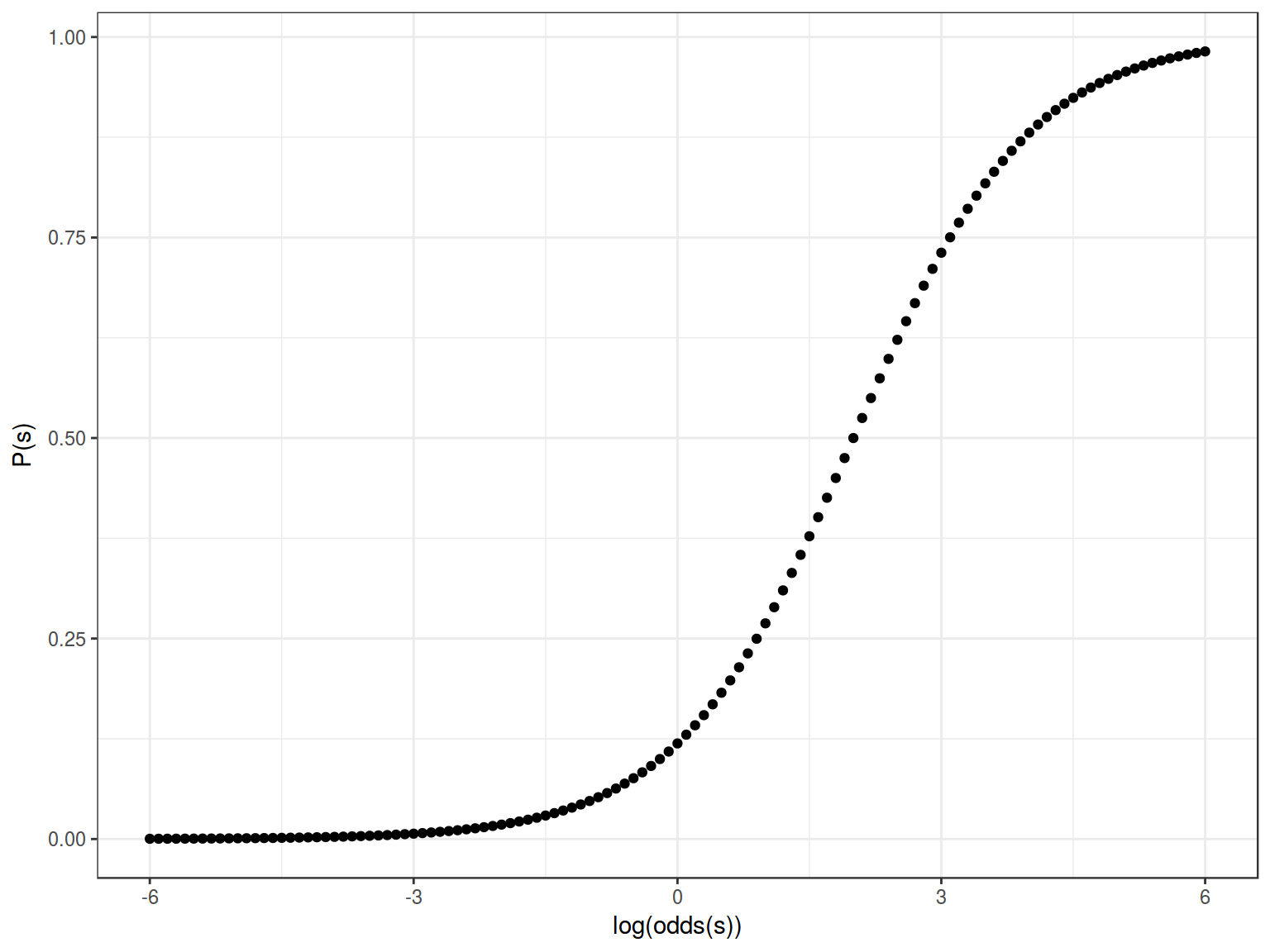
Formula for this sigmoid is the following:

\[y = \frac{1}{1+e^{-(x-2)}}\]

Feeting our logistic regression we should be able to squeeze/stretch center of our sigmoid:

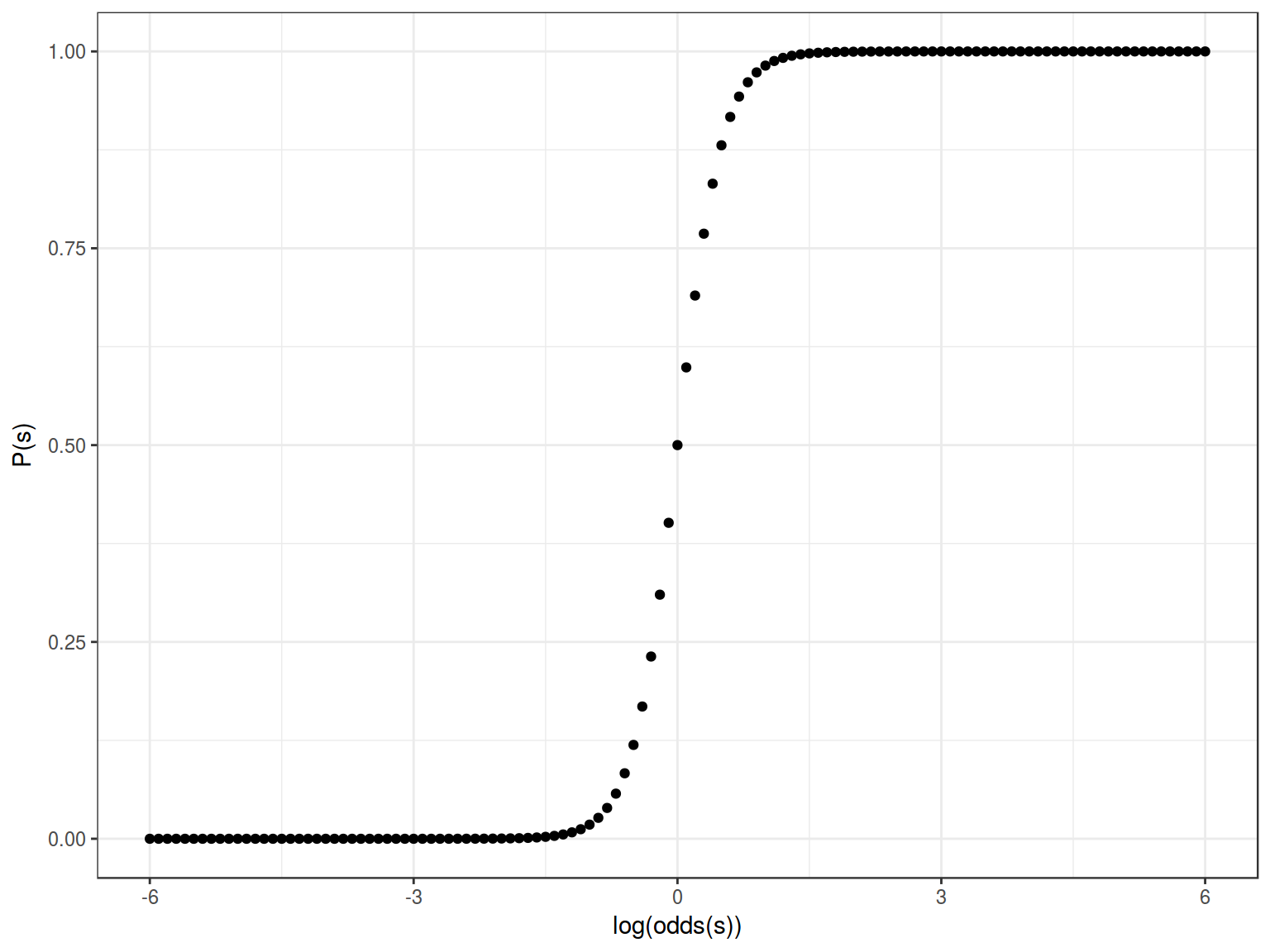
\[y = \frac{1}{1+e^{-4x}}\]

So the more general formula will be: \[y = \frac{1}{1+e^{-k(x-z)}}\]

where

• depending on \(x\) values sigmoid can be reversed
• \(k\) is squeeze/stretch coefficient
• \(z\) is coefficient that indicates movement of the sigmoid center to the left or right side

3.1 Numeric example

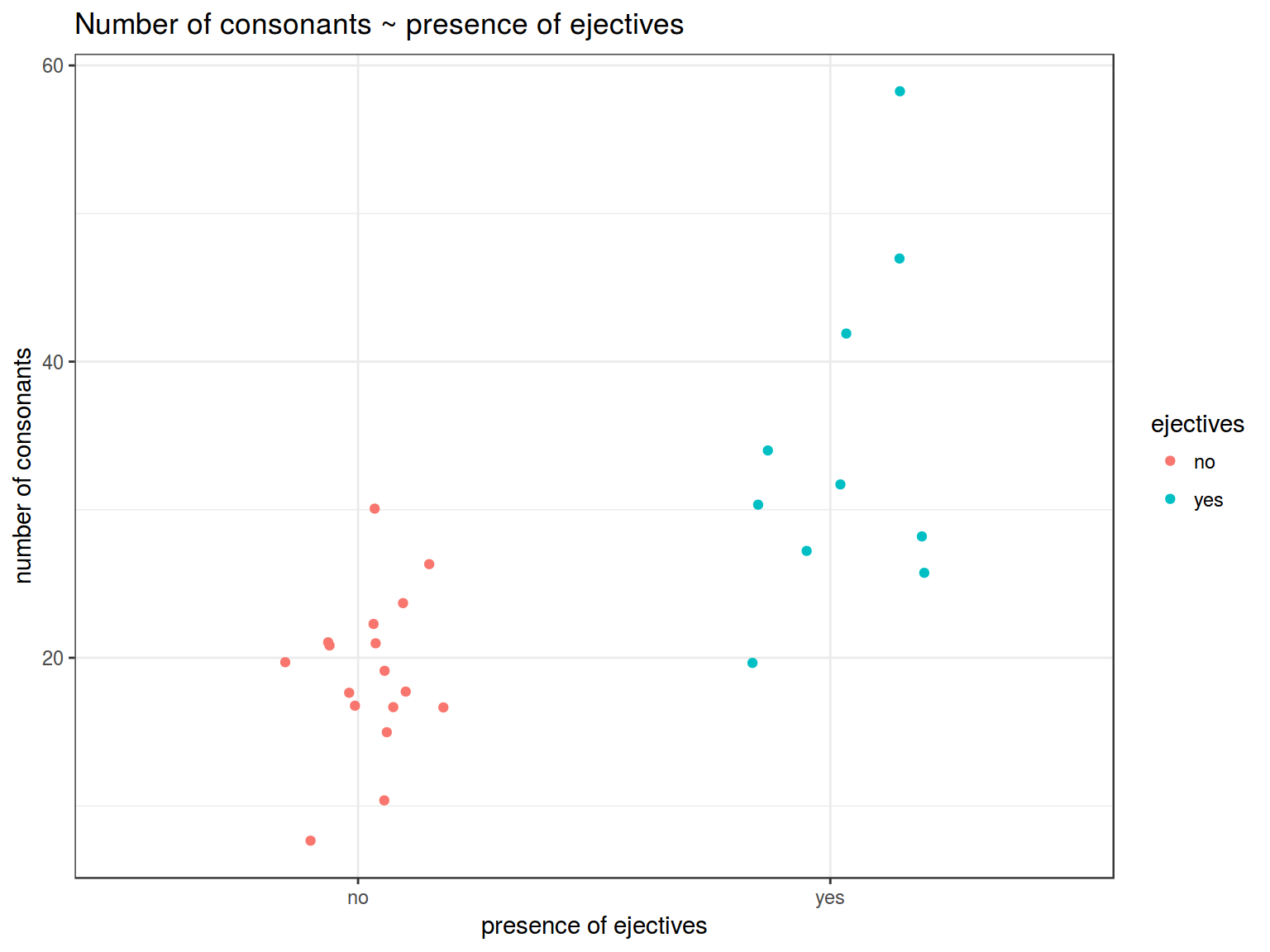
It is interesting, whether languages with ejective sounds have in average more consonants. So I collected data from phonological database LAPSyD: http://goo.gl/0btfKa.

ej_cons <- read.csv("http://goo.gl/0btfKa")
ej_cons %>% 
  ggplot(aes(ejectives, n.cons.lapsyd, color = ejectives))+
  geom_jitter(width = 0.2)+
  labs(title = "Number of consonants ~ presence of ejectives",
       x = "presence of ejectives",
       y = "number of consonants")+
  theme_bw()

• Model without predictors

fit1 <- glm(ejectives~1, data = ej_cons, family = "binomial")
summary(fit1)

## 
## Call:
## glm(formula = ejectives ~ 1, family = "binomial", data = ej_cons)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -0.9619  -0.9619  -0.9619   1.4094   1.4094  
## 
## Coefficients:
##             Estimate Std. Error z value Pr(>|z|)
## (Intercept)  -0.5306     0.3985  -1.331    0.183
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 35.594  on 26  degrees of freedom
## Residual deviance: 35.594  on 26  degrees of freedom
## AIC: 37.594
## 
## Number of Fisher Scoring iterations: 4

How we get this estimate value?

table(ej_cons$ejectives)

## 
##  no yes 
##  17  10

log(10/17)

## [1] -0.5306283

What does this model say? This model says that if we have no predictors and take some language it has \(\frac{0.5306283}{(1+e^{-0.5306283})} = 0.3340993\) probability to have ejectives.

• Model with numeric predictor

fit2 <- glm(ejectives~n.cons.lapsyd, data = ej_cons, family = "binomial")
summary(fit2)

## 
## Call:
## glm(formula = ejectives ~ n.cons.lapsyd, family = "binomial", 
##     data = ej_cons)
## 
## Deviance Residuals: 
##     Min       1Q   Median       3Q      Max  
## -1.8317  -0.4742  -0.2481   0.1914   2.1997  
## 
## Coefficients:
##               Estimate Std. Error z value Pr(>|z|)   
## (Intercept)    -9.9204     3.7699  -2.631   0.0085 **
## n.cons.lapsyd   0.3797     0.1495   2.540   0.0111 * 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for binomial family taken to be 1)
## 
##     Null deviance: 35.594  on 26  degrees of freedom
## Residual deviance: 16.202  on 25  degrees of freedom
## AIC: 20.202
## 
## Number of Fisher Scoring iterations: 6

What does this model say? This model says:

\[\log(odds(ej)) = \beta_o + \beta_1 \times n.cons.lapsyd = -9.9204 + 0.3797 \times n.cons.lapsyd\]

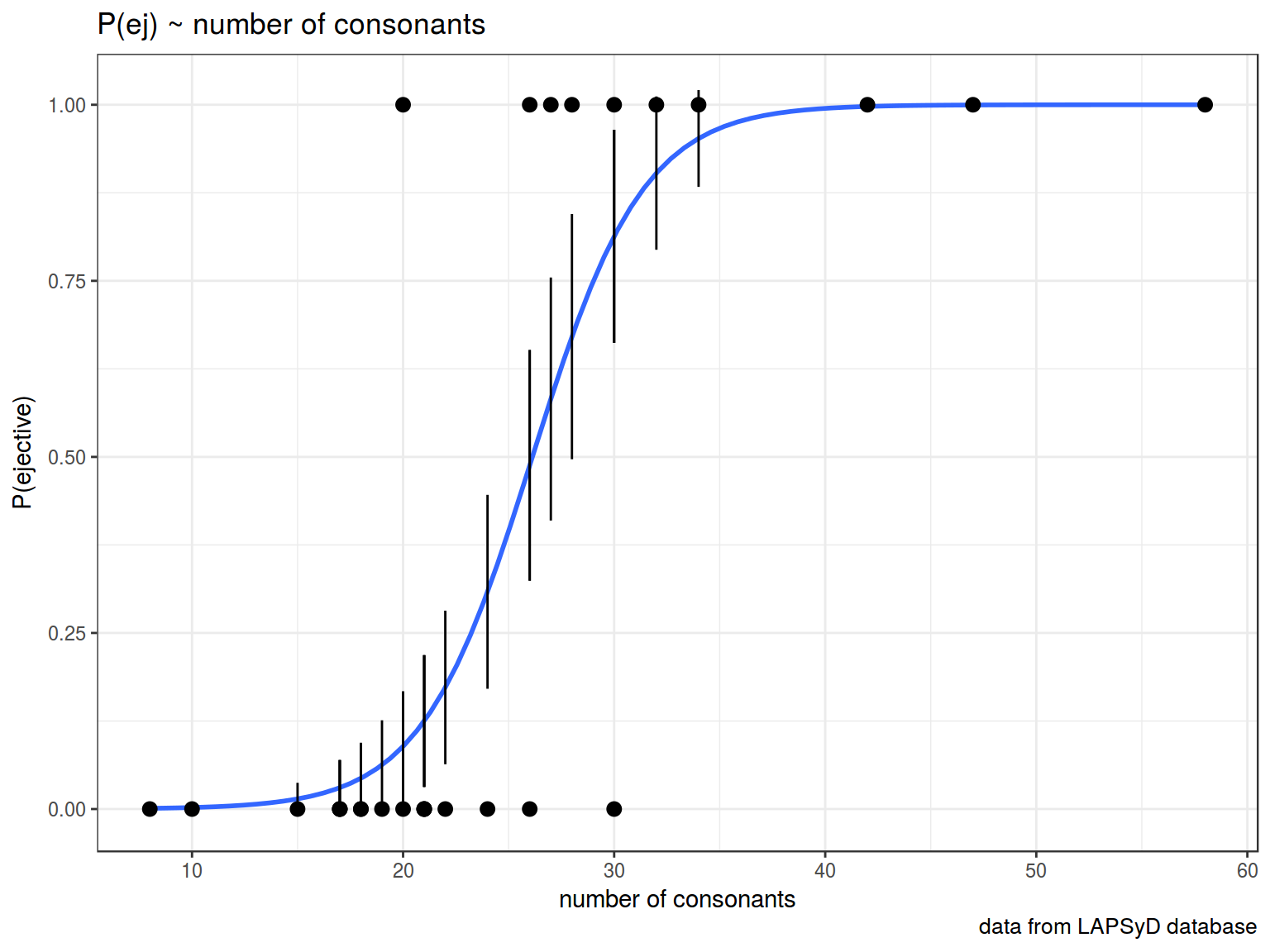
Lets visualize our model:

ej_cons %>% 
  mutate(`P(ejective)` = as.numeric(ejectives) - 1) %>% 
  ggplot(aes(x = n.cons.lapsyd, y = `P(ejective)`))+
  geom_smooth(method = "glm", method.args = list(family = "binomial"), se = FALSE) +
  geom_point()+
  theme_bw()

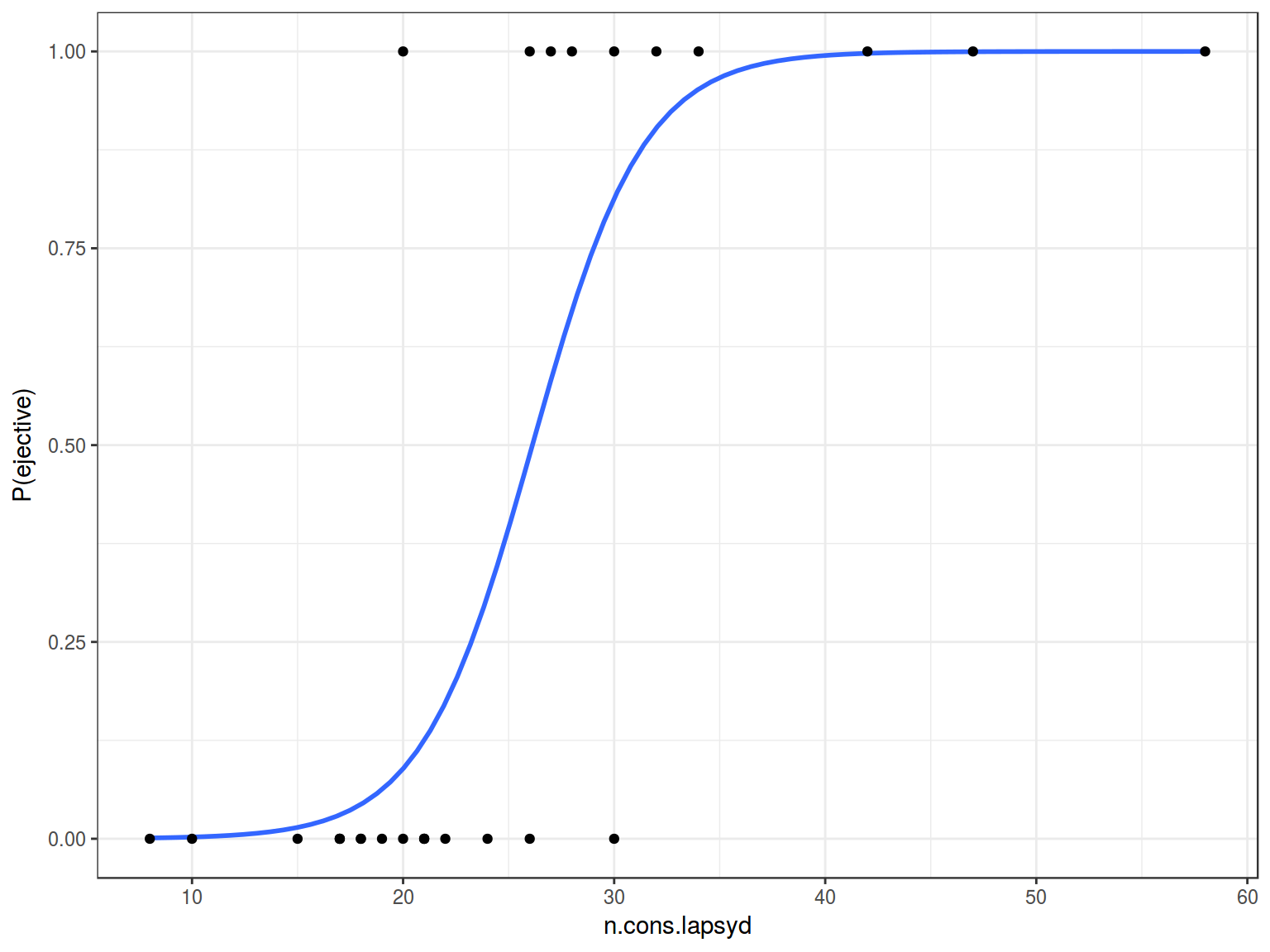
So probability for a language that have 30 consonants will be \[\log(odds(ej)) = -9.9204 + 0.3797 \times 30 = 1.4706\]

\[P(ej) = \frac{1.47061}{1+1.4706}=0.8131486\]

4. predict()

Do we really need to remember all this formulae?

new.df <- data.frame(n.cons.lapsyd = c(30, 55, 34, 10))
predict(fit2, new.df) # odds

##         1         2         3         4 
##  1.470850 10.963579  2.989686 -6.123334

predict(fit2, new.df, type = "response") # probabilities

##           1           2           3           4 
## 0.813186486 0.999982679 0.952106011 0.002186347

predict(fit2, new.df, type = "response", se.fit = TRUE) # probabilities and confidense interval

## $fit
##           1           2           3           4 
## 0.813186486 0.999982679 0.952106011 0.002186347 
## 
## $se.fit
##            1            2            3            4 
## 1.512886e-01 7.882842e-05 6.869366e-02 5.038557e-03 
## 
## $residual.scale
## [1] 1

So we actually can create a plot with confidense intervals.

ej_cons_ci <- cbind.data.frame(ej_cons, predict(fit2, ej_cons, type = "response", se.fit = TRUE)[1:2])
ej_cons_ci

ej_cons_ci %>%
  mutate(`P(ejective)` = as.numeric(ejectives) - 1) %>% 
  ggplot(aes(x = n.cons.lapsyd, y = `P(ejective)`))+
  geom_smooth(method = "glm", method.args = list(family = "binomial"), se = FALSE)+
  geom_point() +
  geom_pointrange(aes(x = n.cons.lapsyd, ymin = fit - se.fit, ymax = fit + se.fit))+
  labs(title = "P(ej) ~ number of consonants",
       x = "number of consonants",
       caption = "data from LAPSyD database")+
  theme_bw()