library(tidyverse)

1.1 Descriptive statistics

homo <- read_csv("http://goo.gl/Zjr9aF")
homo %>% 
  summarise(mean = mean(s.duration.ms),
            trimed_mean = mean(s.duration.ms, trim = 0.2),
            weighted_mean = weighted.mean(s.duration.ms, age),
            median = median(s.duration.ms),
            min = min(s.duration.ms),
            max = max(s.duration.ms),
            sd = sd(s.duration.ms))
summary(homo)
##    speaker          s.duration.ms   vowel.duration.ms average.f0.Hz  
##  Length:14          Min.   :45.13   Min.   : 93.68    Min.   :100.3  
##  Class :character   1st Qu.:58.15   1st Qu.:118.31    1st Qu.:116.0  
##  Mode  :character   Median :61.93   Median :123.75    Median :122.7  
##                     Mean   :61.22   Mean   :124.06    Mean   :125.2  
##                     3rd Qu.:64.51   3rd Qu.:132.27    3rd Qu.:130.3  
##                     Max.   :78.11   Max.   :147.52    Max.   :155.3  
##   f0.range.Hz     perceived.as.homo perceived.as.hetero
##  Min.   : 37.40   Min.   : 4.00     Min.   : 4.00      
##  1st Qu.: 53.30   1st Qu.: 8.25     1st Qu.: 5.00      
##  Median : 73.20   Median :12.50     Median :12.50      
##  Mean   : 76.66   Mean   :13.50     Mean   :11.50      
##  3rd Qu.:102.53   3rd Qu.:20.00     3rd Qu.:16.75      
##  Max.   :118.20   Max.   :21.00     Max.   :21.00      
##  perceived.as.homo.percent orientation             age       
##  Min.   :0.16              Length:14          Min.   :19.00  
##  1st Qu.:0.33              Class :character   1st Qu.:22.75  
##  Median :0.50              Mode  :character   Median :28.50  
##  Mean   :0.54                                 Mean   :27.86  
##  3rd Qu.:0.80                                 3rd Qu.:30.00  
##  Max.   :0.84                                 Max.   :40.00

1.2 Common words

Statistics are used much like a drunk uses a lamppost: for support, not illumination. A.E. Housman (commonly attributed to Andrew Lang)

test parameters:

2. One sample test

2.1 Confident interval

\[\bar{x} \pm z \times \frac{\sigma}{\sqrt{n}}\]

Where is standard error?

z — z-score, for 95% CI it is 1.96, for 99% CI it is 2.58

homo %>% 
  summarise(mean = mean(s.duration.ms),
            ci = 1.96 * sd(s.duration.ms)/sqrt(n()),
            min = mean - ci,
            max = mean + ci,
            x = "duration of [s]")
homo %>% 
  summarise(mean = mean(s.duration.ms),
            ci = 1.96 * sd(s.duration.ms)/sqrt(n()),
            min = mean - ci,
            max = mean + ci,
            x = "duration of [s]") %>% 
  ggplot(aes(x, mean, ymin = min, ymax = max))+
  geom_pointrange()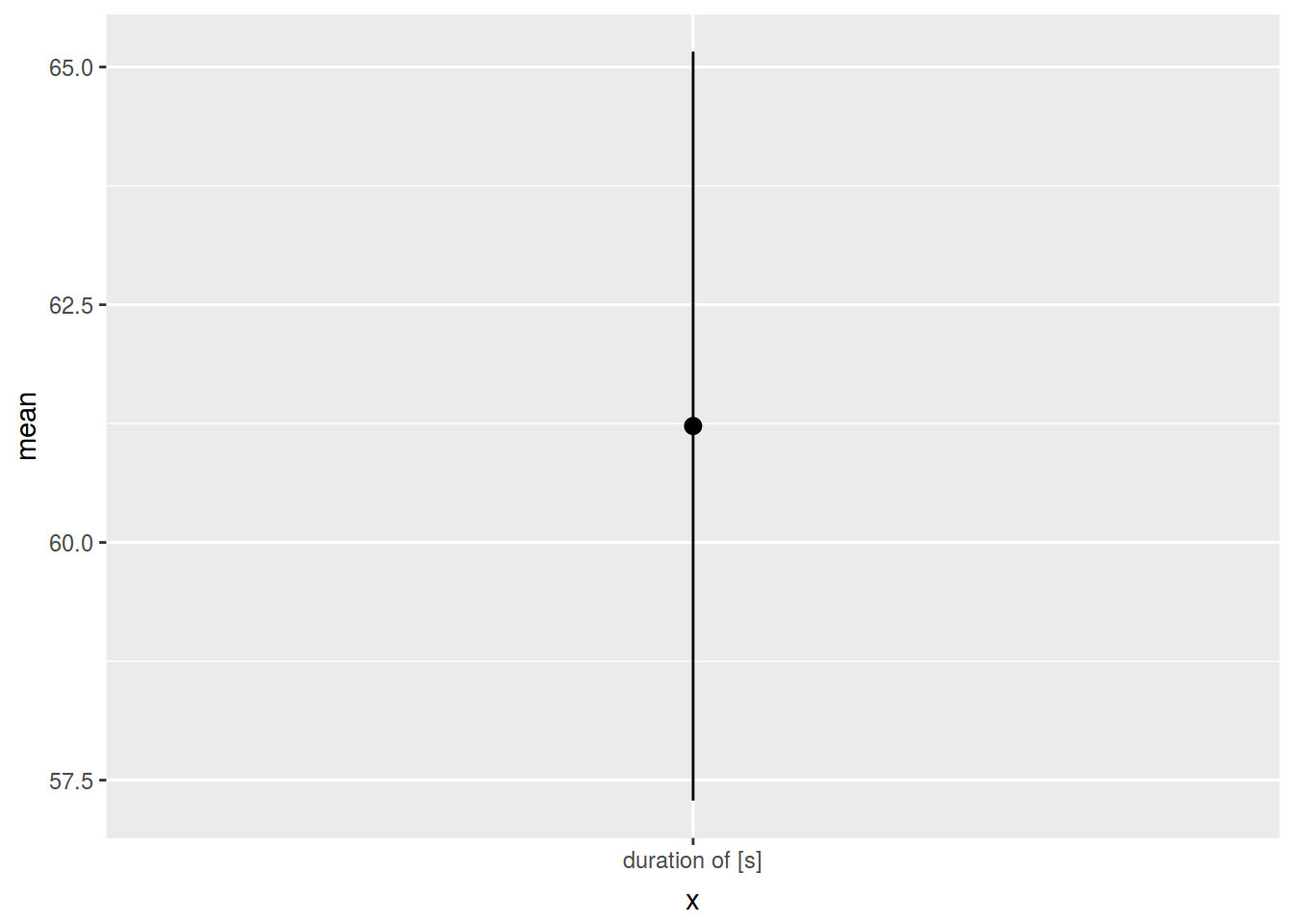

  #geom_errorbar() # For pure line
  #geom_linerange() # For line with borders

2.2 One sample t-test

In some article I found out that mean [s] duration for Chineese is 56 ms. Is the data from [Hau 2007] provides statistically significant difference?

\[t = \frac{\bar{x}-\mu_0}{\sigma/\sqrt{n}}\]

\(\sigma\) — standard deviation

homo %>% 
  summarise(t_statistics = (mean(s.duration.ms)-56)/(sd(s.duration.ms)/sqrt(n())),
            df = n() - 1,
            p_value = 2*pt(-abs(t_statistics),df=df))
t.test(homo$s.duration.ms, mu = 56)
## 
##  One Sample t-test
## 
## data:  homo$s.duration.ms
## t = 2.5997, df = 13, p-value = 0.02202
## alternative hypothesis: true mean is not equal to 56
## 95 percent confidence interval:
##  56.88292 65.56565
## sample estimates:
## mean of x 
##  61.22429

2.3 Normality

one sample t-test assumes:

How to check?

homo %>% 
  ggplot(aes(s.duration.ms))+
  geom_density()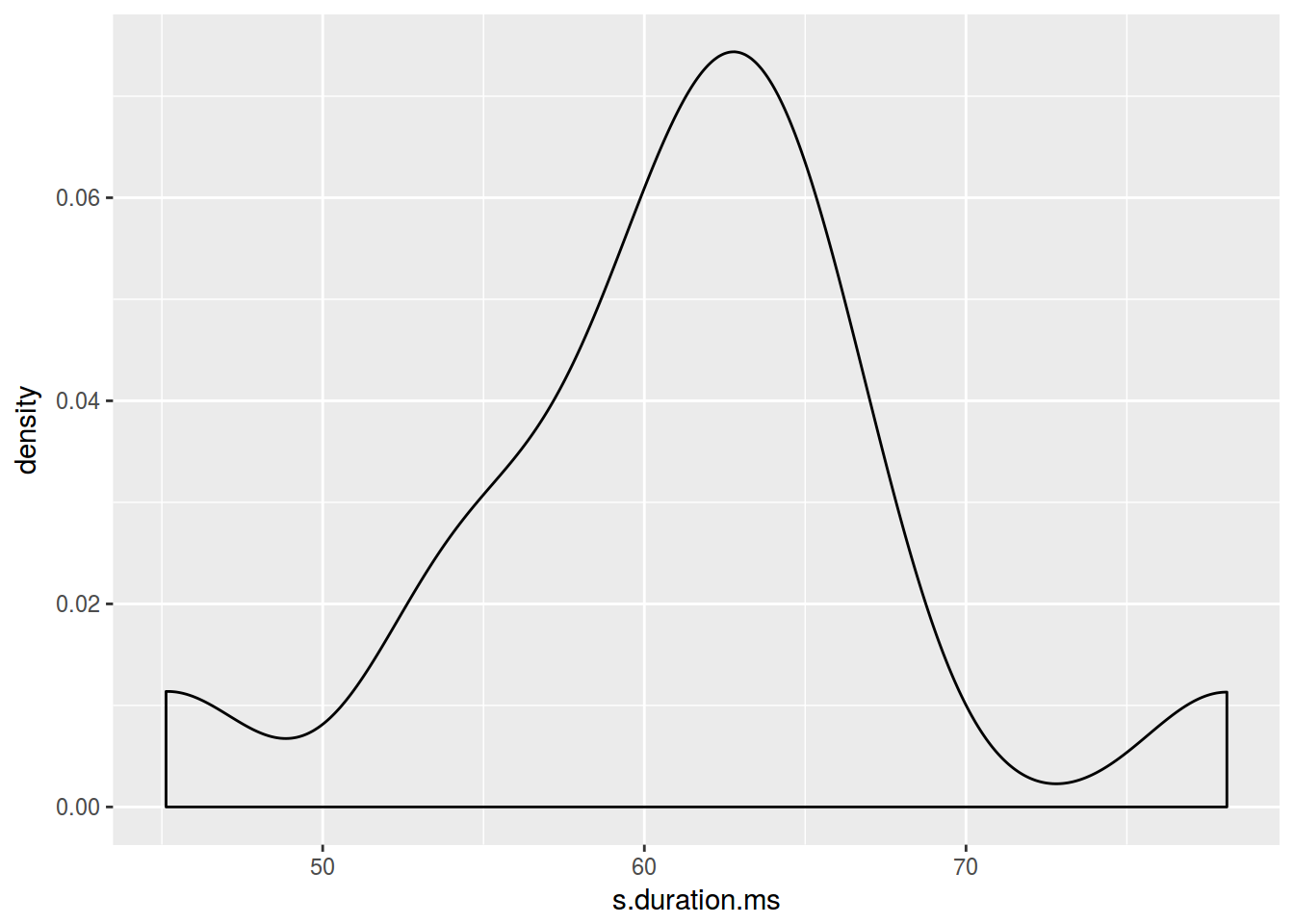

library(sm)
sm.density(homo$s.duration.ms, model = "Normal", col.band="yellowgreen")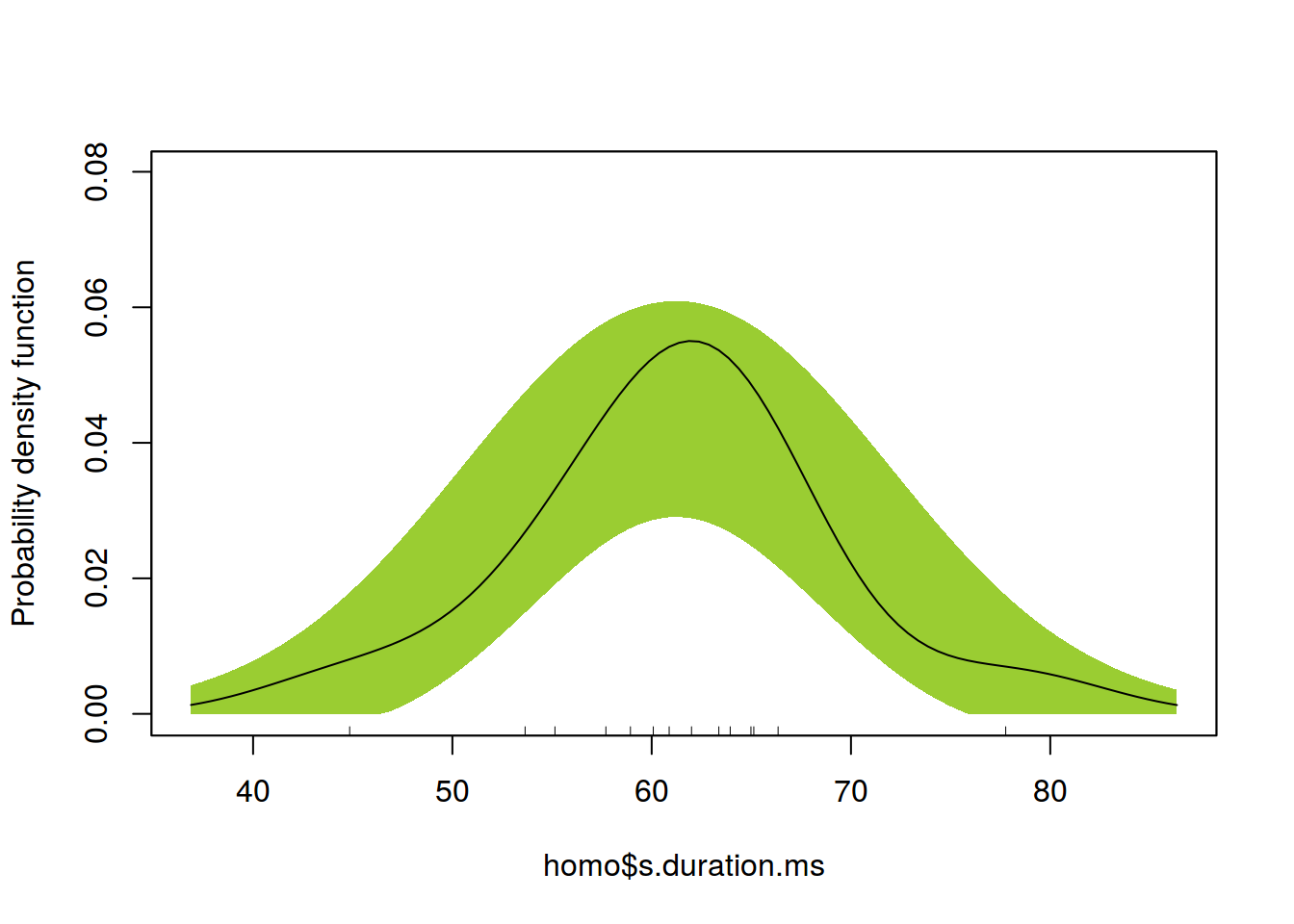

homo %>% 
  ggplot(aes(sample = s.duration.ms))+
  geom_qq()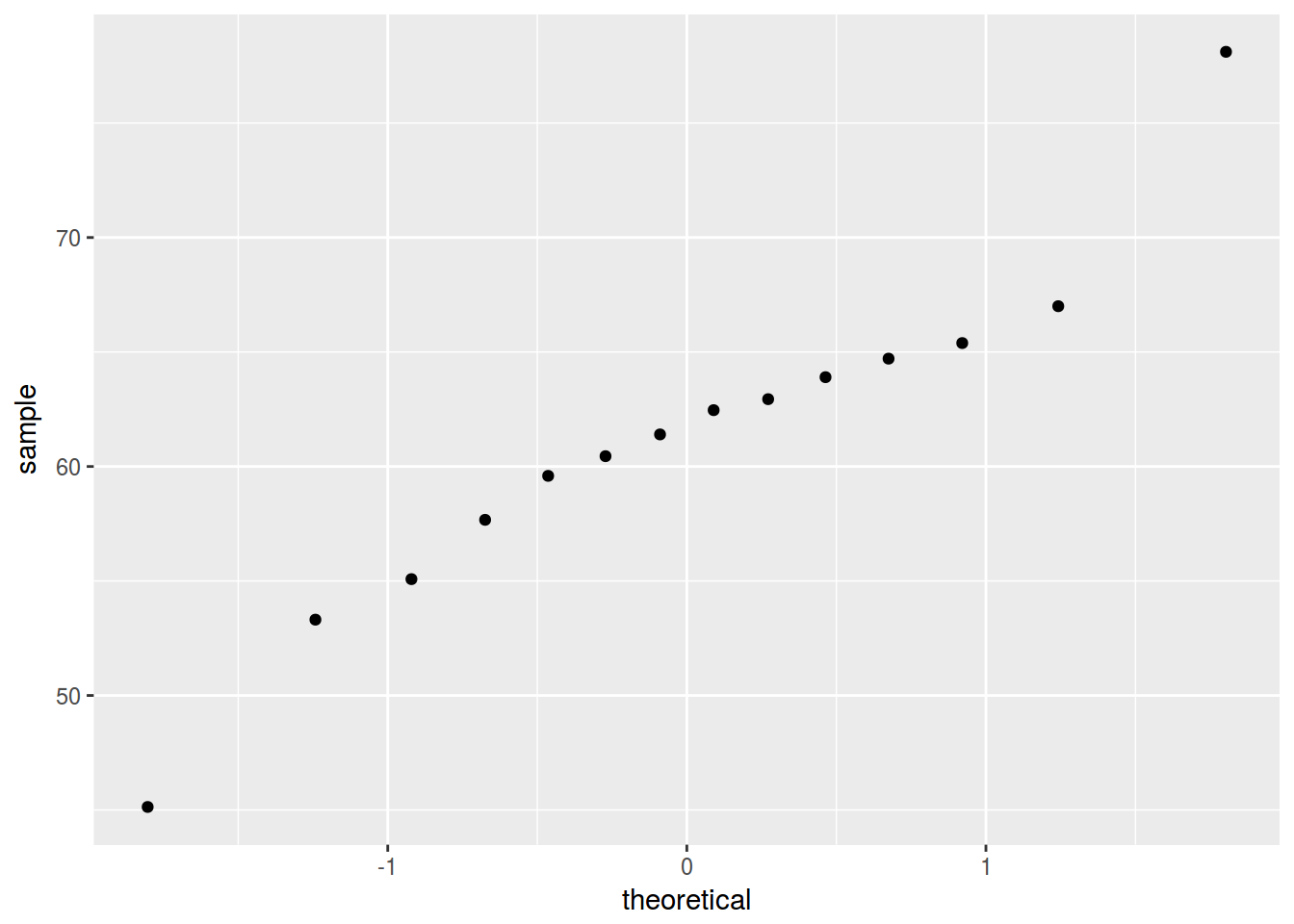

2.5 Wilcoxon test

What if your data is not normally distributed?

wilcox.test(homo$s.duration.ms, mu = 56)
## 
##  Wilcoxon signed rank test
## 
## data:  homo$s.duration.ms
## V = 89, p-value = 0.02026
## alternative hypothesis: true location is not equal to 56

3. Two sample test

3.1 Two sample t-test

What if we have two samples?

t.test(s.duration.ms~orientation, data = homo)
## 
##  Welch Two Sample t-test
## 
## data:  s.duration.ms by orientation
## t = -1.4263, df = 11.994, p-value = 0.1793
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -13.945621   2.911336
## sample estimates:
## mean in group hetero   mean in group homo 
##             58.46571             63.98286

3.2 Paired t-test

What if we samples are dependent?

df
t.test(df$before, df$after, paired = TRUE)
## 
##  Paired t-test
## 
## data:  df$before and df$after
## t = 10.919, df = 31, p-value = 3.765e-12
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  2.598141 3.791602
## sample estimates:
## mean of the differences 
##                3.194871

3.3 Wilcoxon test

wilcox.test(s.duration.ms~orientation, data = homo)
## 
##  Wilcoxon rank sum test
## 
## data:  s.duration.ms by orientation
## W = 16, p-value = 0.3176
## alternative hypothesis: true location shift is not equal to 0
wilcox.test(df$before, df$after, paired = TRUE)
## 
##  Wilcoxon signed rank test
## 
## data:  df$before and df$after
## V = 526, p-value = 1.397e-09
## alternative hypothesis: true location shift is not equal to 0

4. Multiple sample tests → next lecture

5. Multiple comparisons problem

xkcd Significant. Explonation. This colled: data dredging, data fishing, data snooping, equation fitting, p-hacking…

If m independent comparisons are performed, the family-wise error rate (FWER), is given by

\[\alpha = 1 - (1 - \alpha_{for\ each\ pair})^m\] \[\alpha = 1 - (1 - 0.05)^{21} = 1- 0.34 = 0.66\]

5.1 Adjustment for multiple tests

x <- c(0.04, 0.03, 0.01)
p.adjust(x, method = 'bonferroni') # Bonferroni correction
## [1] 0.12 0.09 0.03
p.adjust(x, method = 'holm')
## [1] 0.06 0.06 0.03
p.adjust(x, method = 'BH')
## [1] 0.04 0.04 0.03
p.adjust(x, method = 'BY')
## [1] 0.07333333 0.07333333 0.05500000

For conclusion

p-value is not so loved anymore…





© О. Ляшевская, И. Щуров, Г. Мороз, code on GitHub