1. Распределения

library(tidyverse)

1. Распределения в R

В R встроено какое-то количество известных распределений. Все они представлены четырьмя функциями:

d... (функция плотности, probability density function),
p... (функция распределения, cumulative distribution function) — интеграл площади под кривой от начала до указанной квантили
q... (обратная функции распределения, inverse cumulative distribution function) — значение p-той квантили распределения
и r... (рандомные числа из заданного распределения).

Рассмотрим все это на примере нормального распределения.

tibble(x = 1:100,
           PDF = dnorm(x = x, mean = 50, sd = 10)) %>% 
  ggplot(aes(x, PDF))+
  geom_point()+
  labs(title = "PDF нормального распределения (μ = 50, sd = 10)")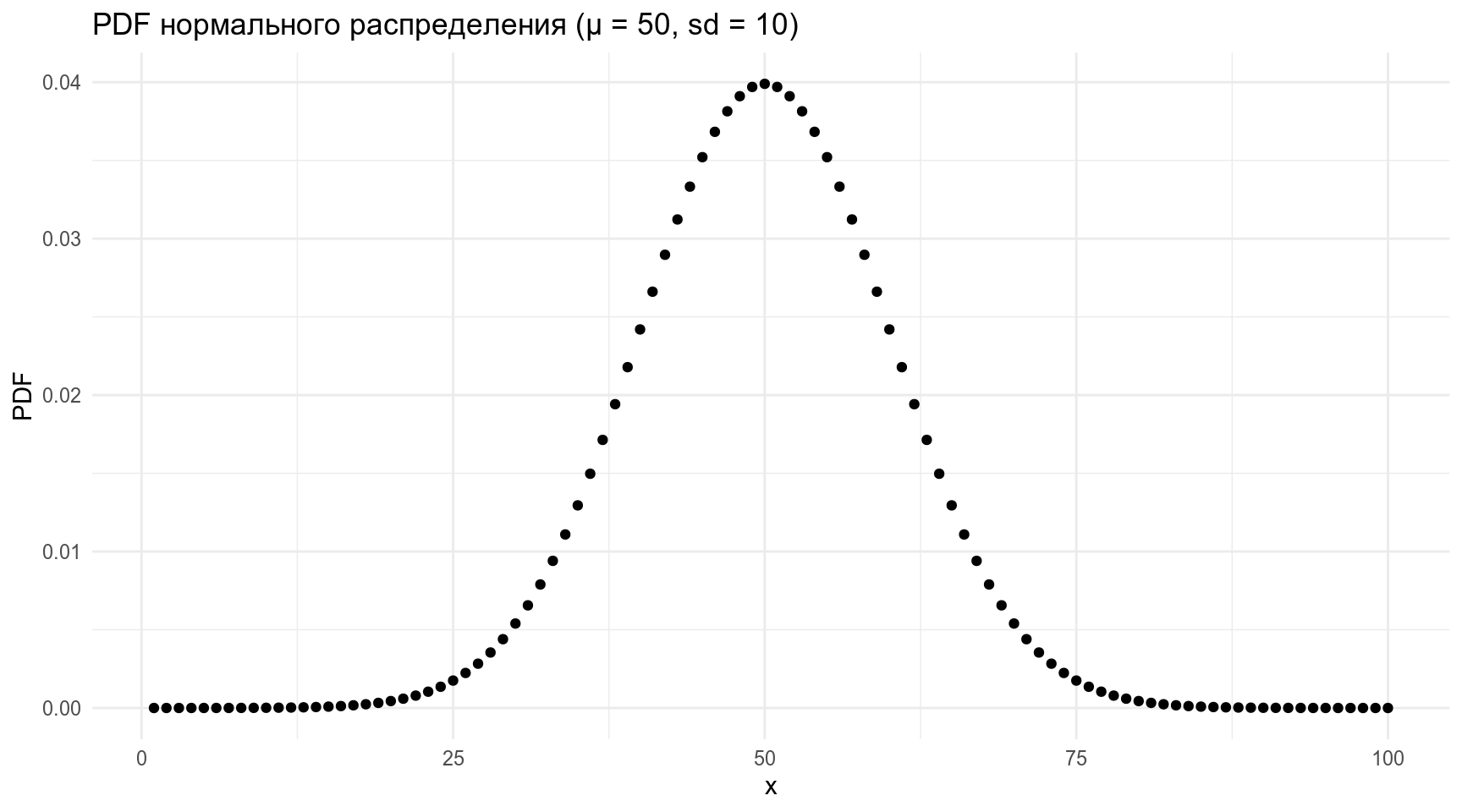

Какое количество данных лежит в промежутке от 0 до 30?

pnorm(30, mean = 50, sd = 10)

[1] 0.02275013

tibble(x = 1:100,
           CDF = pnorm(x, mean = 50, sd = 10)) %>% 
  ggplot(aes(x, CDF))+
  geom_point()+
  labs(title = "CDF нормального распределения (μ = 50, sd = 10)")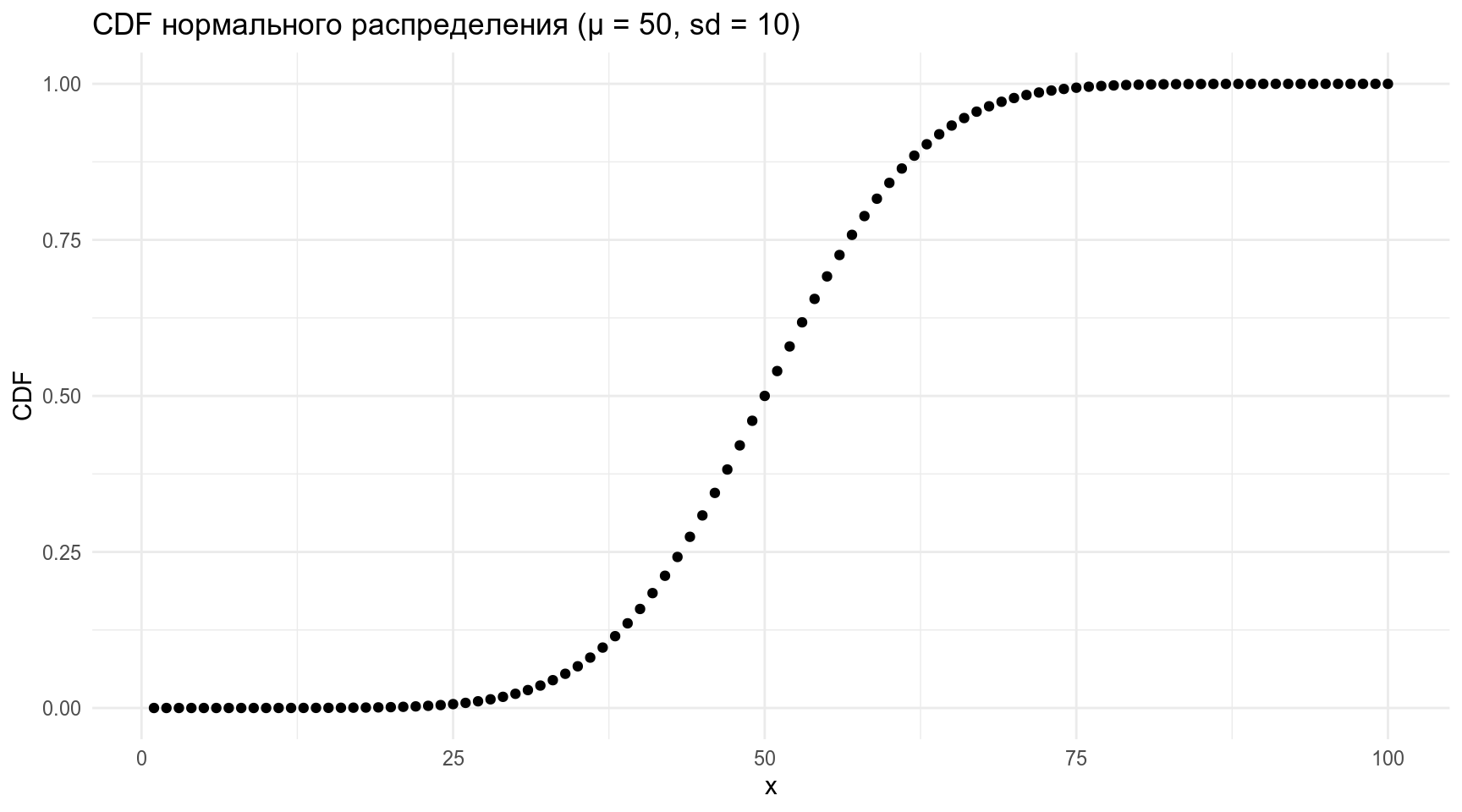

Какое значение соответствует 40-ой квантили?

qnorm(0.4, mean = 50, sd = 10)

[1] 47.46653

tibble(quantiles = seq(0, 1, by = 0.01),
           value = qnorm(quantiles, mean = 50, sd = 10)) %>% 
  ggplot(aes(quantiles, value))+
  geom_point()+
  labs(title = "inverse CDF нормального распределения (μ = 50, sd = 10)")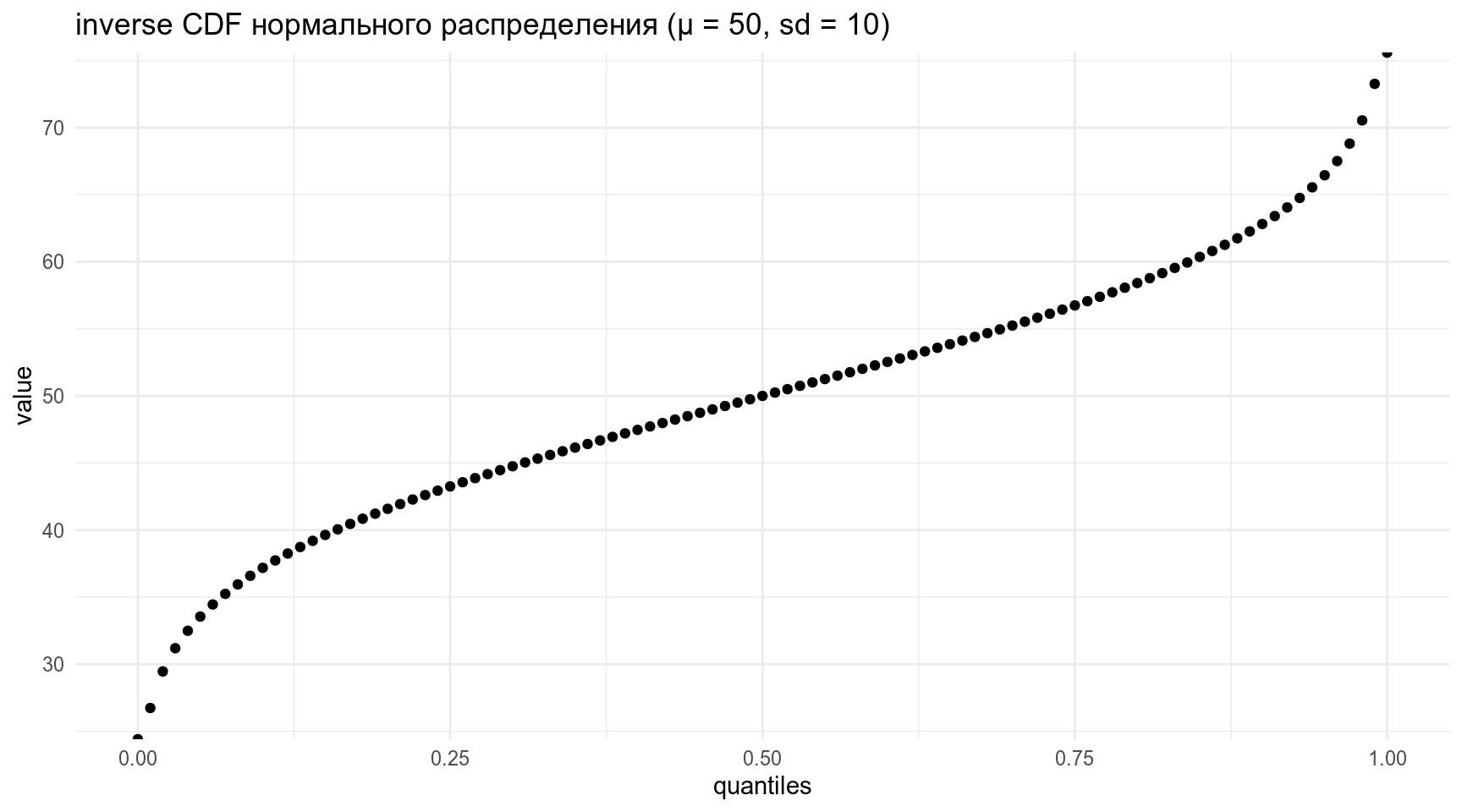

~~Siri, Алиса,~~ Дорогой R, сгенерируй мне 100 наблюдений из нормального распределения со средним 50 и стандартным отклонением 10.

tibble(sample = rnorm(100, mean = 50, sd = 10)) %>% 
  ggplot(aes(sample))+
  geom_histogram()+
  labs(title = "выборка нормально распределенных чисел (μ = 50, sd = 10)")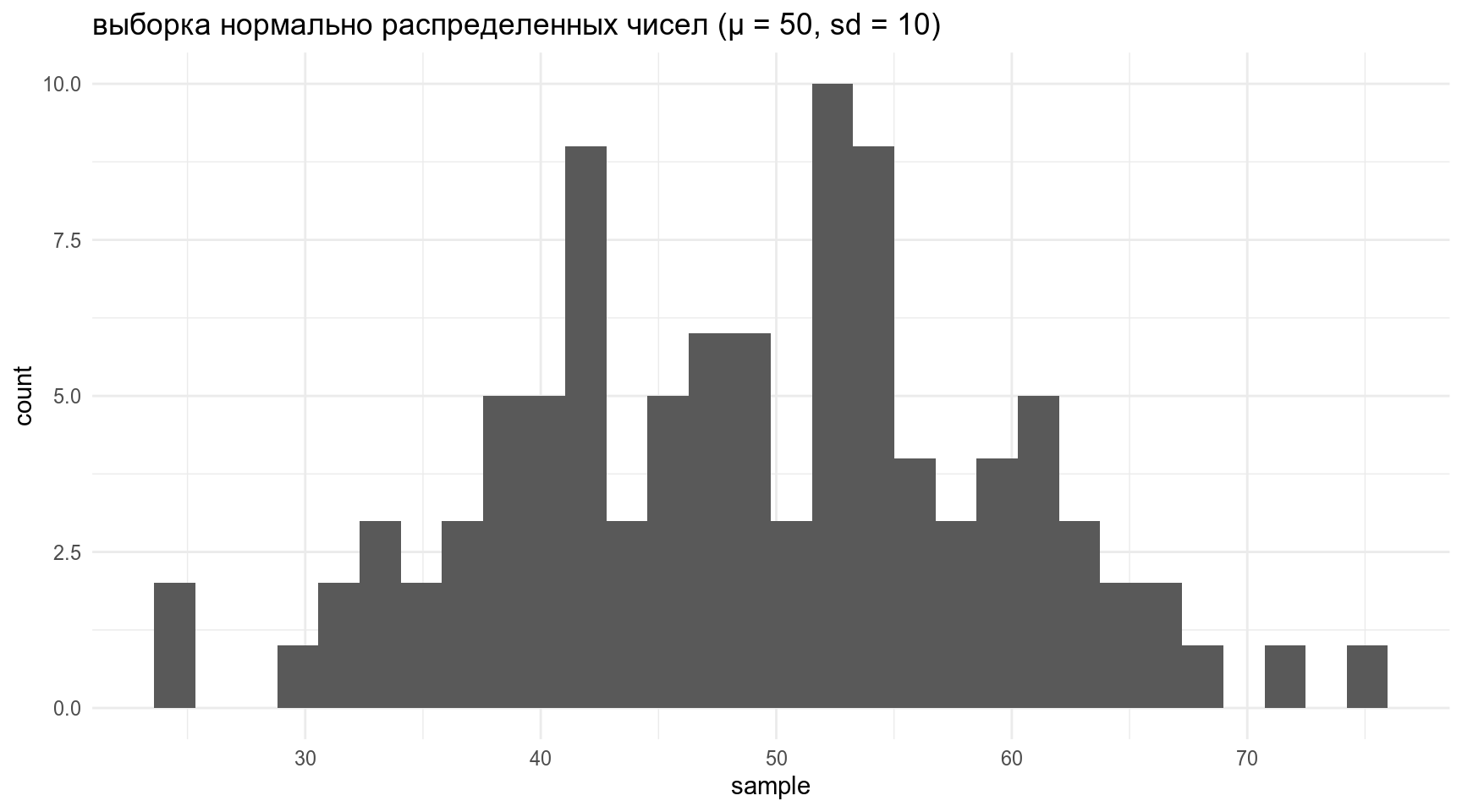

Если не использовать set.seed(), то результат работы рандомизатора нельзя будет повторить.

1.1

Какое значение имеет 25% квантиль нормального распределения со средним в 20 и стандартным отклонением 90.

1.2

Посчитайте z-score для 97% квантили нормально распределенных данных.

2. Дискретные распределения

2.1 Биномиальное распределение

Биномиальное распределение — распределение количетсва успехов эксперементов Бернулли из n попыток с вероятностью успеха p.

\[P(k | n, p) = \frac{n!}{k!(n-k)!} \times p^k \times (1-p)^{n-k} = {n \choose k} \times p^k \times (1-p)^{n-k}\] \[ 0 \leq p \leq 1; n, k > 0\]

tibble(x = 0:50,
           density = dbinom(x = x, size = 50, prob = 0.16)) %>% 
  ggplot(aes(x, density))+
  geom_point()+
  geom_line()+
  labs(title = "Биномиальное распределение p = 0.16, n = 50")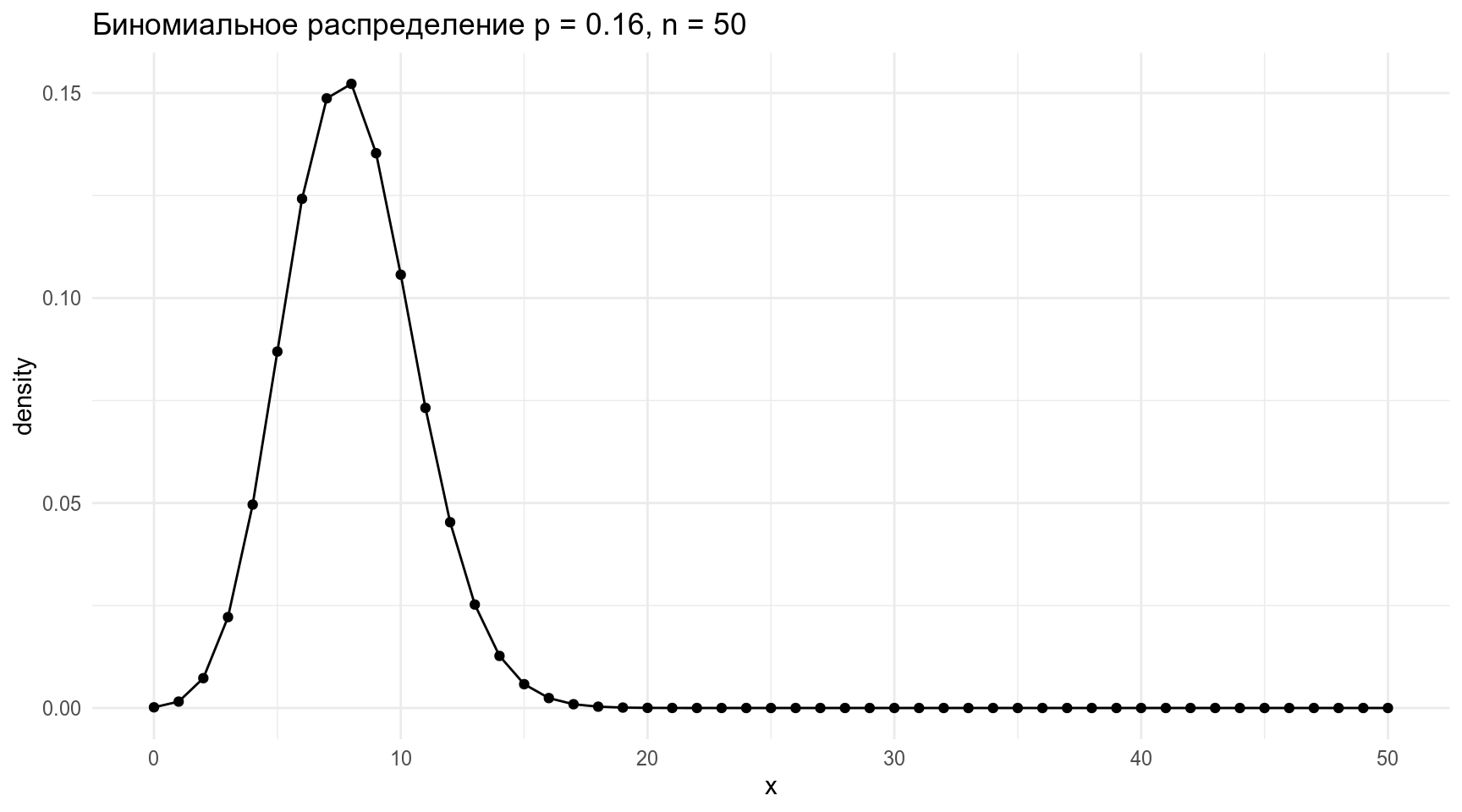

2.2 Геометрическое распределение

Геометрическое распределение — распределение количетсва эксперементов Бернулли с вероятностью успеха p до первого успеха.

\[P(k | p) = (1-p)^k\times p\] \[k\in\{1, 2, \dots\}\]

tibble(x = 0:50,
           density = dgeom(x = x, prob = 0.16)) %>% 
  ggplot(aes(x, density))+
  geom_point()+
  geom_line()+
  labs(title = "Геометрическое распределение p = 0.16, n = 50")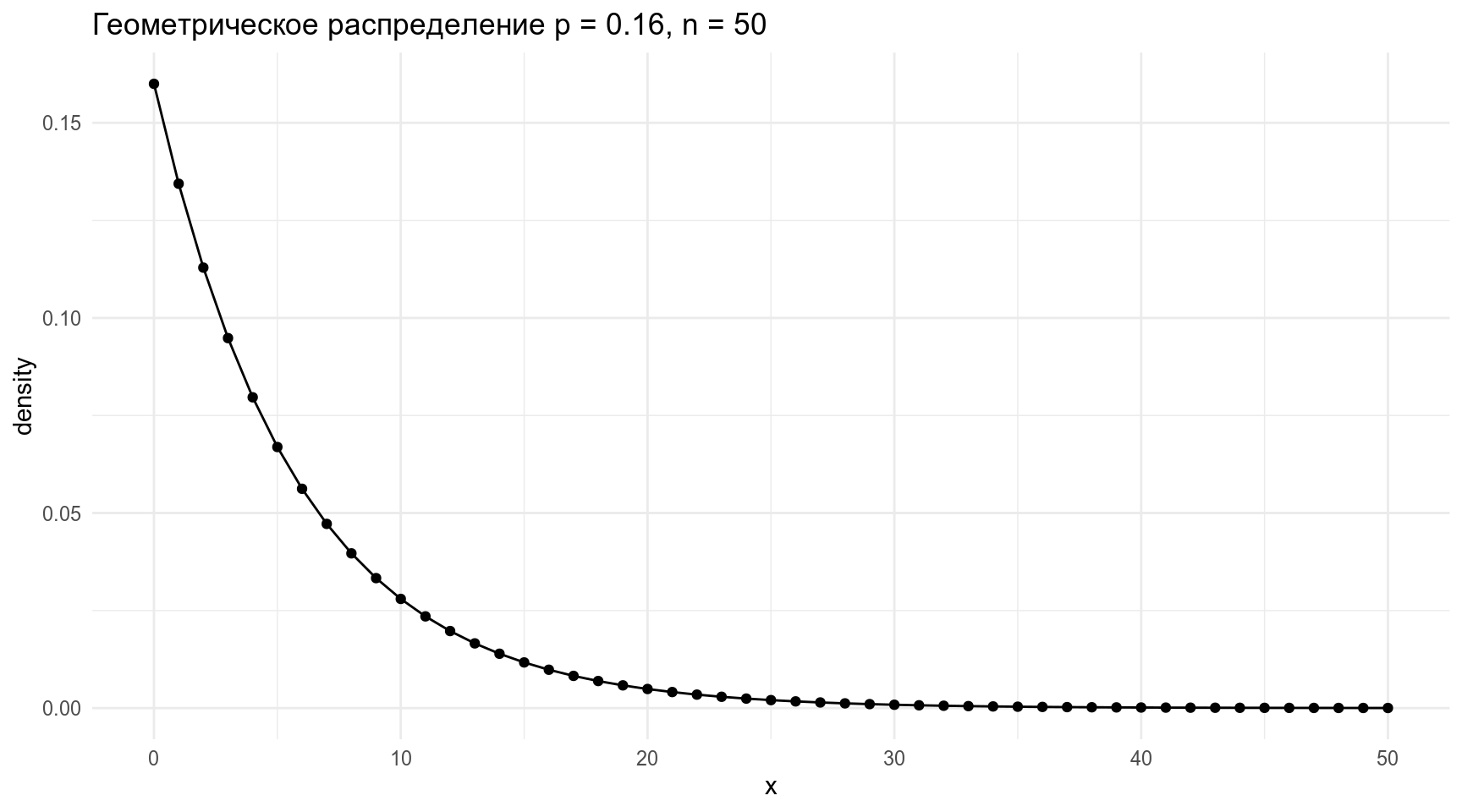

2.3 Распределение Пуасона

Распределение Пуассона — распределение числа событий, произошедших за фиксированное время при условии, что данные события происходят с некоторой фиксированной средней интенсивностью (\(\lambda\)) и независимы друг от друга.

\[P(Y = k) = \frac{\lambda^k}{k!} \times e^{-\lambda}\] \[k\in\{1, 2, \dots\}, \lambda \in \{0, -\infty\}\]

tibble(x = 0:50,
           density = dpois(x = x, lambda =  5)) %>% 
  ggplot(aes(x, density))+
  geom_point()+
  geom_line()+
  labs(title = "Распределение Пуасона с мат. ожиданием λ = 5")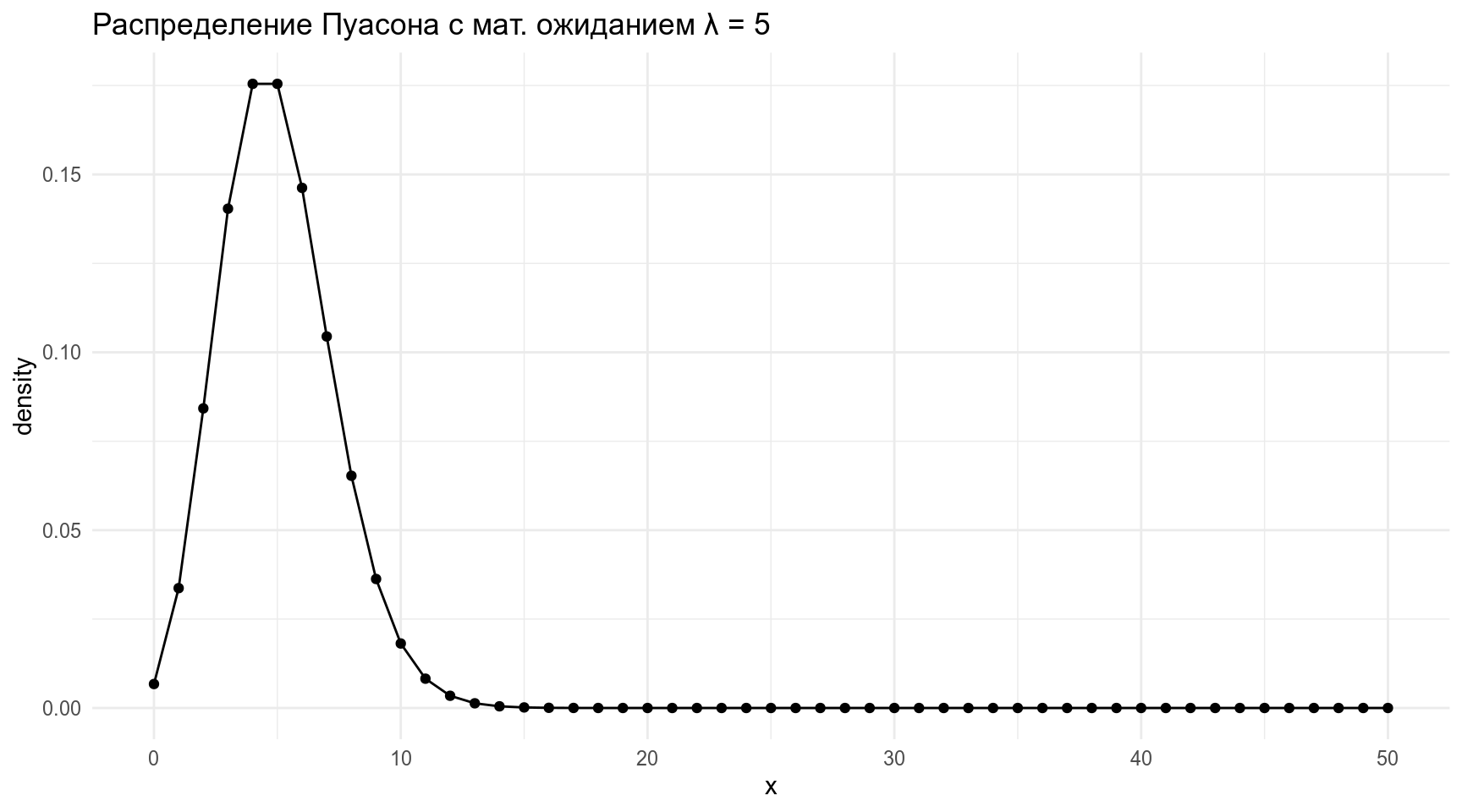

2.3.1

Используя вот этот датасет и функцию glm() с аргументом family=poisson, постройте регрессию, предсказывающую количество наград (num_awards), которые получат студенты на основе типа программы (prog) и оценки их экзамена по математике (math). Если записать датасет в переменную df, а модель в переменную model, следующий код должен делать следующий график:

df %>% 
  mutate(predictions = predict(model, type = "response")) %>% 
  ggplot(aes(x = math, y = predictions, color = prog)) +
  geom_point(aes(y = num_awards), position=position_jitter(h=.1)) +
  geom_line() +
  labs(x = "math score", y = "expected number of awards",
       caption = "data from https://stats.idre.ucla.edu/r/dae/poisson-regression/")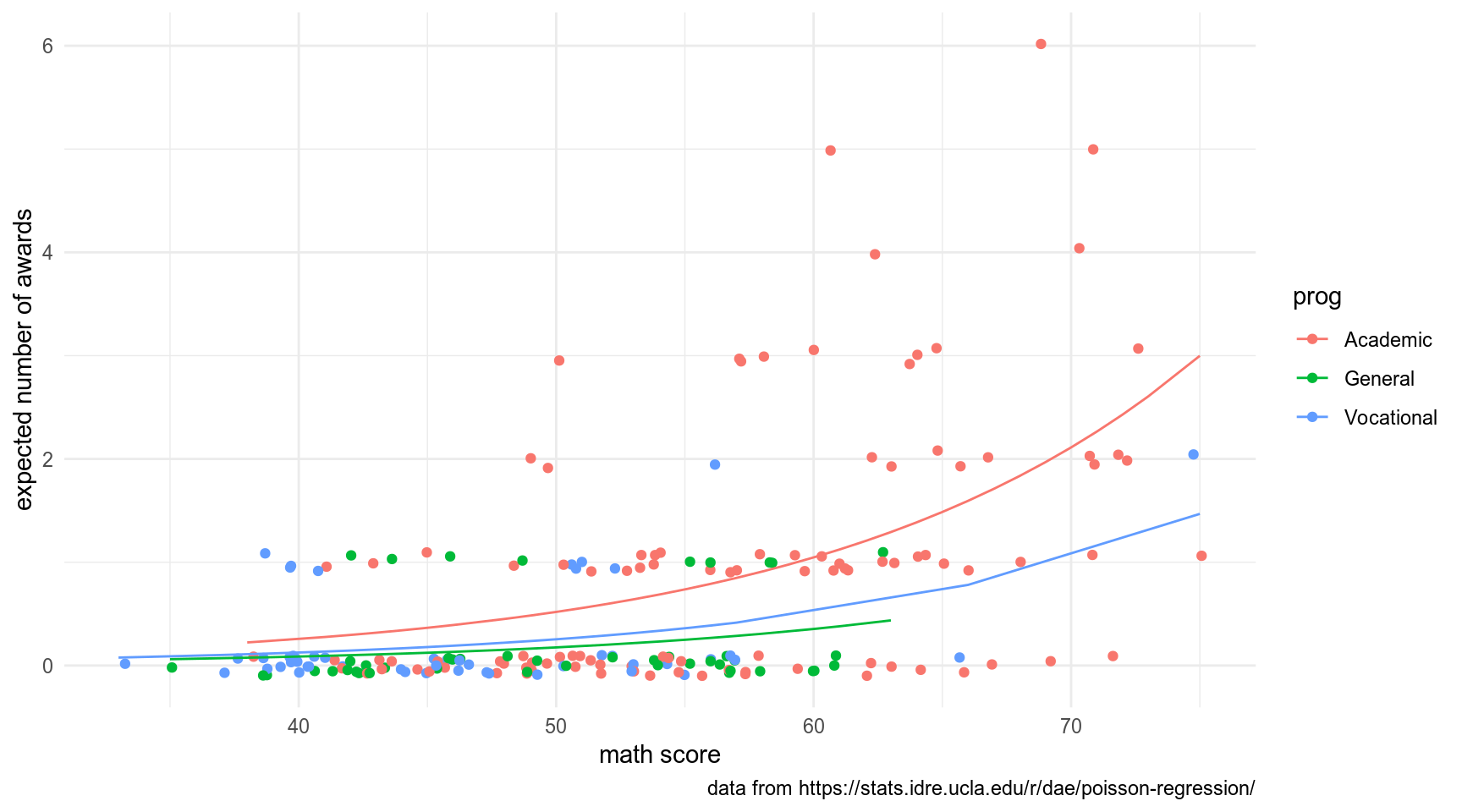

2.4 Мультиномиальное распределение

Мультиномиальное распределение — обобщение биноимального эксперимента на случай n независимых испытаний с k исходами с вероятностями каждого исхода \(p_1, p_2, \dots p_k\).

\[P(x_1, \dots, x_k | n, p_1, \dots p_k) = \frac{n!}{x_1!\times\dots\times x_k!} \times p_1^{x_1}\times\dots\times p_2^{x_k}\] \[ x_i \in \{0, n\}, i \in \{1, k\}, \sum_{i=1}^kx_i = n \]

Если у нас есть три взаимисключающих исхода V1, V2 и V3 с верятностями \(p_1 = 0.4, p_2 = 0.35\) и \(p_3 = 0.25\), какова вероятность получить V1 7 раз, V2 3 раза и V3 2 раза?

dmultinom(x = c(7, 3, 2), prob = c(0.4, 0.35, 0.25))

[1] 0.03477197

А как выглядит распределение?

library(ggtern)
rep(1:10, 3) %>% 
  combn(., 3) %>% 
  t() %>% 
  as.data.frame() %>% 
  rowwise() %>% 
  mutate(multinomial = dmultinom(c(V1, V2, V3), prob = c(0.6, 0.3, 0.1))) %>%
  ggplot(aes(x = V1, y = V2, z = V3, color = multinomial)) +
  coord_tern()+
  geom_point(size = 0.3)+
  scale_color_continuous(low = "grey90", high = "black") +
  scale_L_continuous(labels = c("", "2", "4", "6", "8", "10"))+
  scale_R_continuous(labels = c("", "2", "4", "6", "8", "10"))+
  scale_T_continuous(labels = c("", "2", "4", "6", "8", "10"))+
  labs(title = "Мультиномиальное распределение для трех исходов (0.6, 0.3, 0.1)")+
  theme_bw()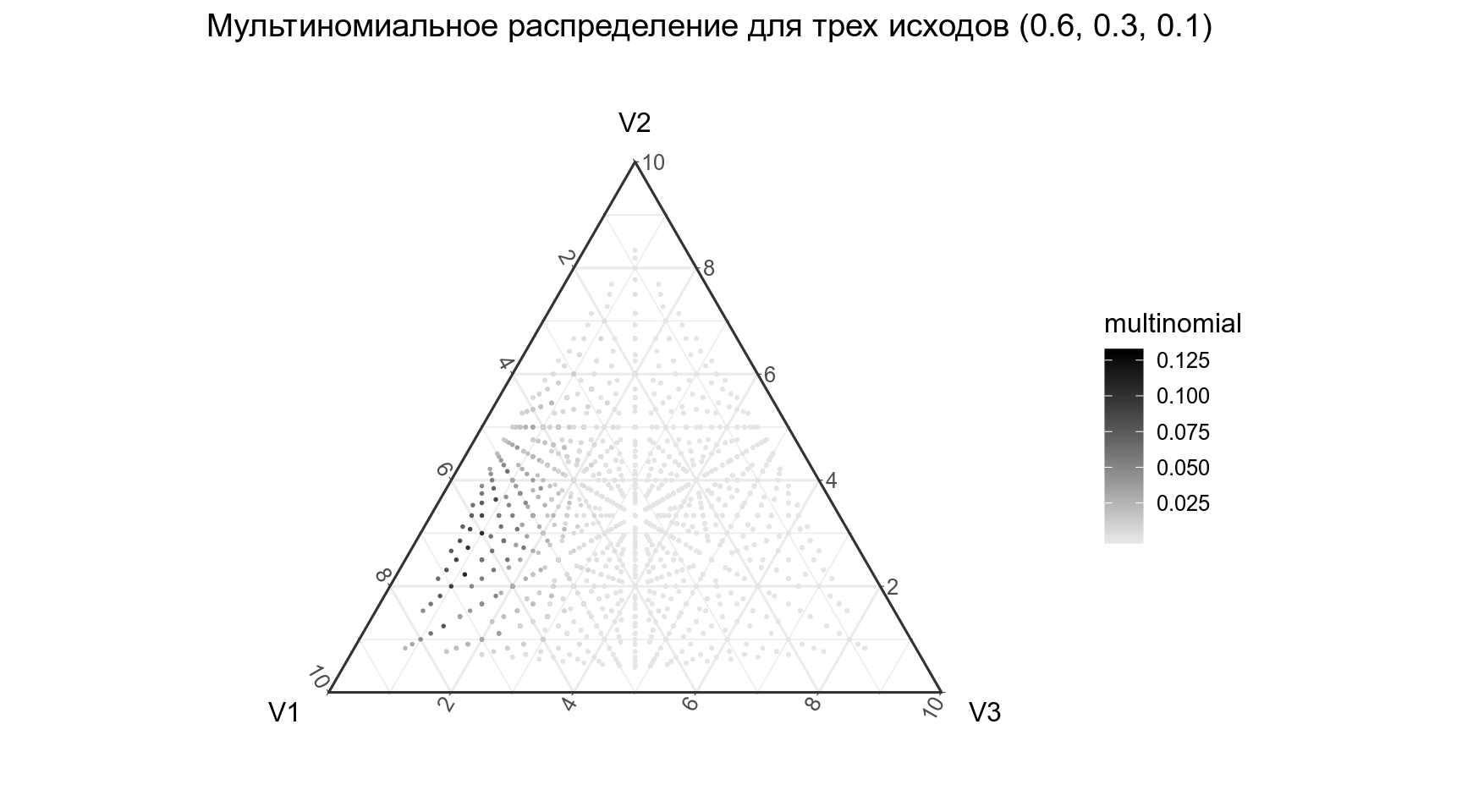

3. Непрерывные распределения

3.1 Нормальное распределение

\[P(x) = \frac{1}{\sigma\sqrt{2\pi}}\times e^{-\frac{\left(x-\mu\right)^2}{2\sigma^2}}\]

\[\mu \in \mathbb{R}; \sigma^2 > 0\]

tibble(x = 1:100,
           PDF = dnorm(x = x, mean = 50, sd = 10)) %>% 
  ggplot(aes(x, PDF))+
  geom_point()+
  geom_line()+
  labs(title = "PDF нормального распределения (μ = 50, sd = 10)")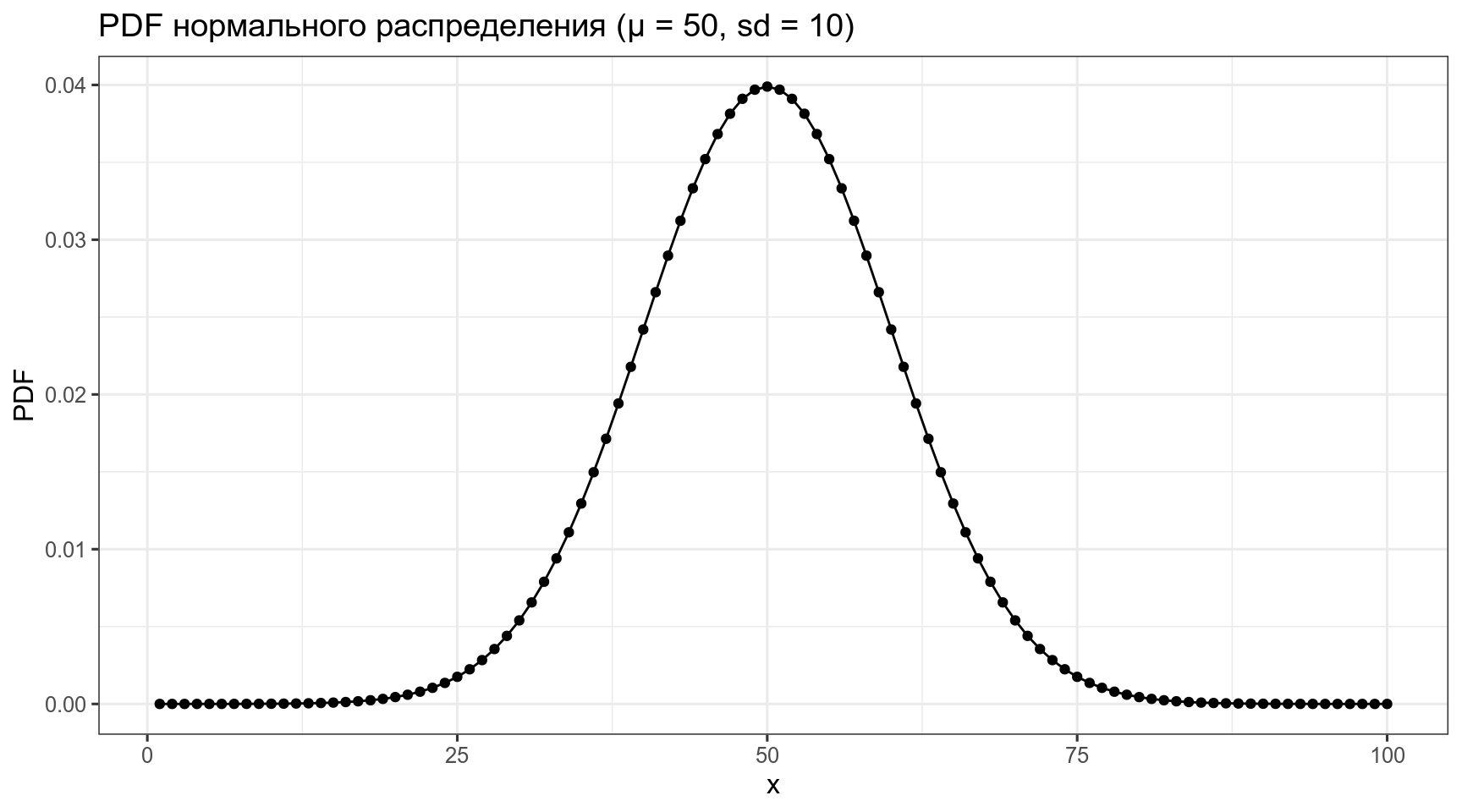

3.2 Логнормальное распределение

\[P(x) = \frac{1}{\sqrt{x\sigma2\pi}}\times e^{-\frac{\left(\ln(x)-\mu\right)^2}{2\sigma^2}}\]

\[\mu \in \mathbb{R}; \sigma^2 > 0\]

tibble(x = 1:100,
           PDF = dlnorm(x = x, meanlog = 3, sdlog = 0.5)) %>% 
  ggplot(aes(x, PDF))+
  geom_point()+
  geom_line()+
  labs(title = "PDF логнормального распределения (μ = 4, sd = 0.5)")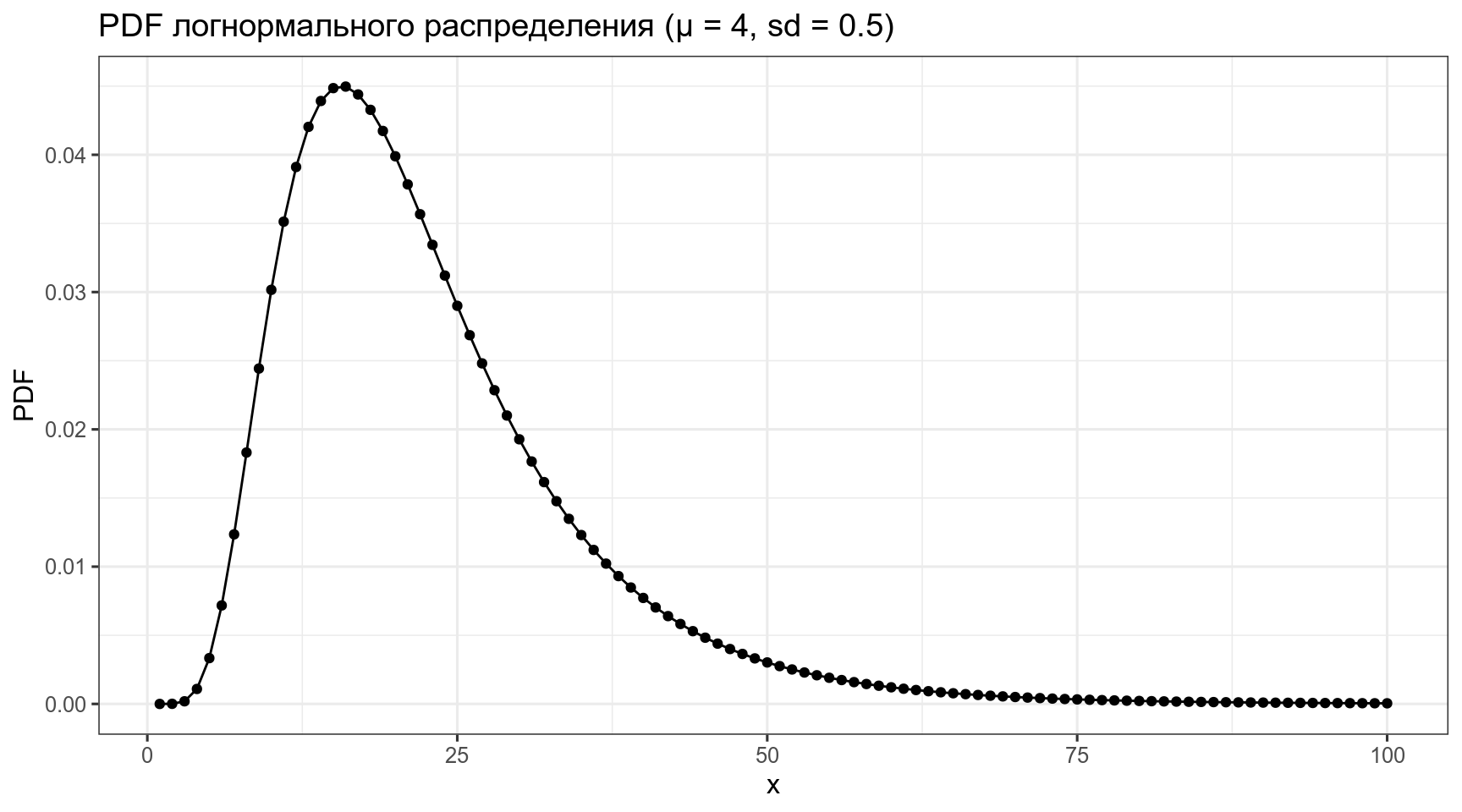

3.3 Экспоненциальное распределение

\[P(x)= \lambda \times e^{-\lambda x}\] \[\lambda > 0\]

tibble(x = 1:20,
           PDF = dexp(x = x, rate = 0.5)) %>% 
  ggplot(aes(x, PDF))+
  geom_point()+
  geom_line()+
  labs(title = "PDF экспоненциального распредления с коэффициентом интенсивности 0.5")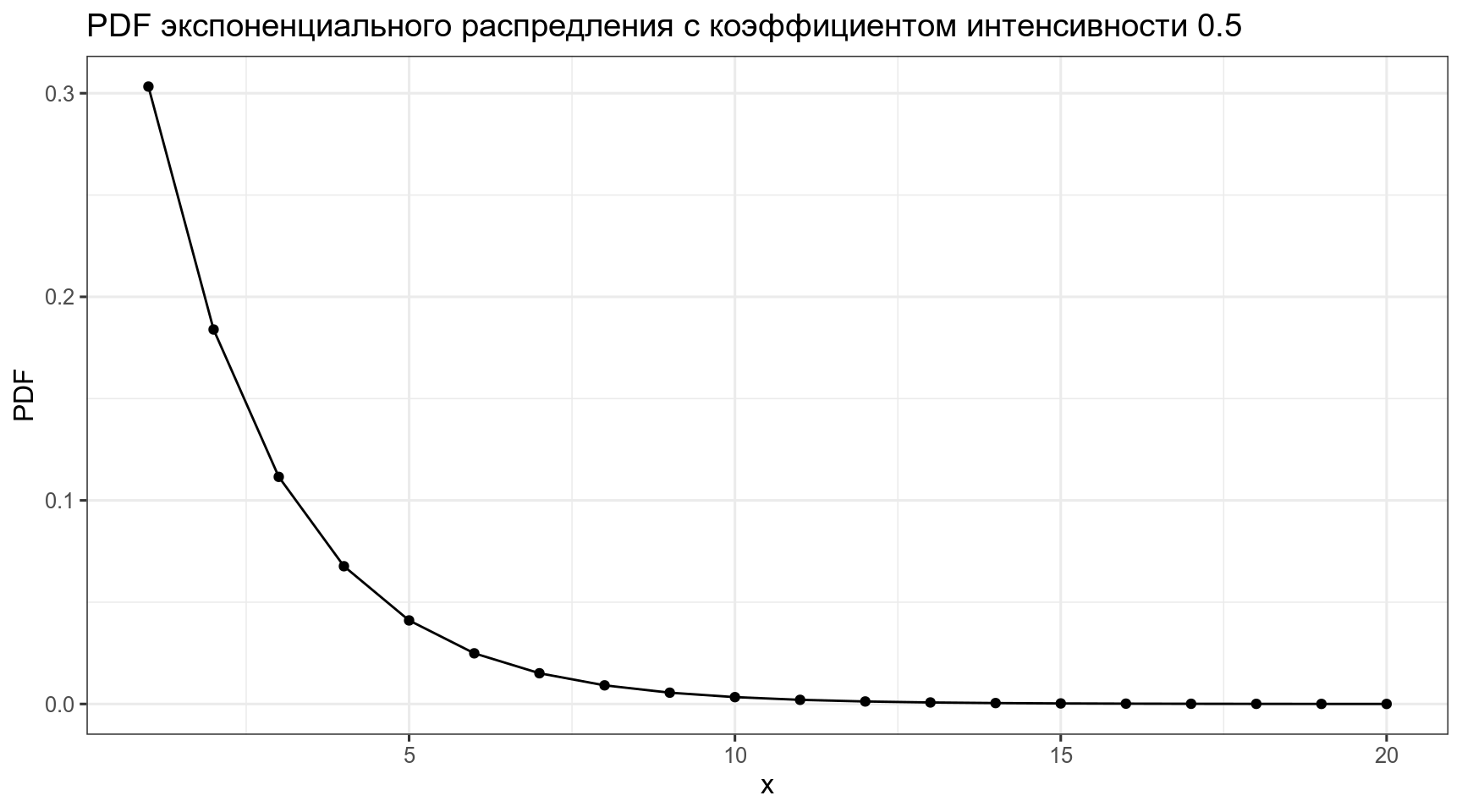

3.4 Распределение Коши

tibble(x = seq(-8, 8, 0.1),
           PDF = dcauchy(x = x, location = 1, scale = 1)) %>% 
  ggplot(aes(x, PDF))+
  geom_point()+
  geom_line()+
  labs(title = "PDF распредления Коши с коэффициентами сдвига и масштаба равные 1")

3.5 Унимодальное распределение

tibble(x = c(5, 5:10),
           PDF = dunif(x = x, min = 5, max = 10)) %>% 
  ggplot(aes(x, PDF))+
  geom_point()+
  geom_line()+
  labs(title = "PDF унимодального распредления (min = 5, max = 10)")

4. Conjugate priors

В байесовском подоходе статистический вывод описывается формулой Байеса

\[P(θ|Data) = \frac{P(Data|θ)\times P(θ)}{P(Data)}\]

\(P(Data|θ)\) — функция правдоподобия (likelihood)
\(P(θ)\) — априорная вероятность (prior)
\(P(Data)\) — данные
\(P(θ|Data)\) — апостериорная вероятность (posterior)

Мы вернемся к формуле Байеса и байесовскому подходу в следующих лекциях, а сейчас важно обсудить распределения априорной и апостериорной вероятностей. Оба эти распределения — распределения вероятностей.

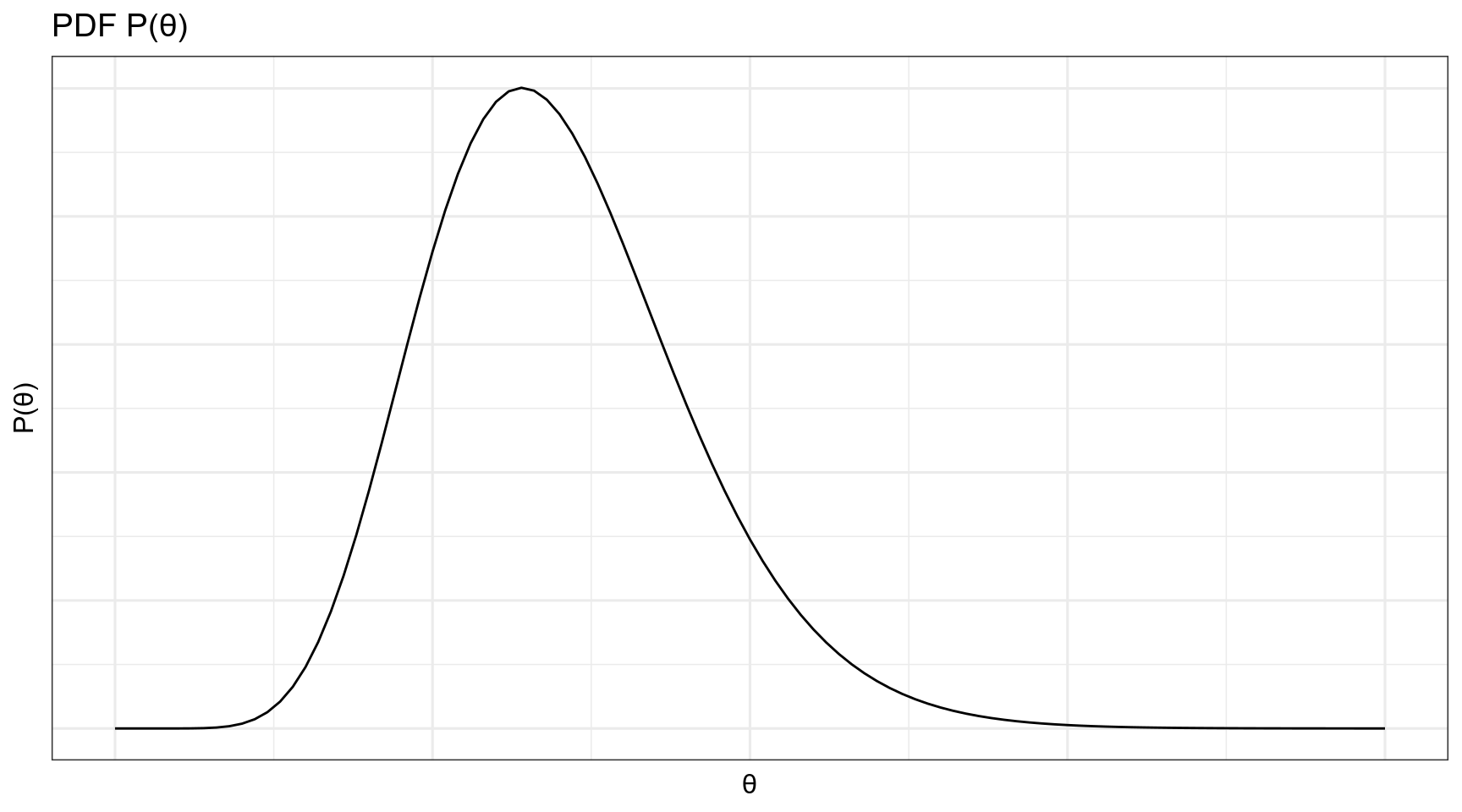
Если у нас есть некоторые данные с функцией правдоподобия P(Data|θ), а априорное и апостериорное распределения θ относятся к одному семейству распределений, то данное семейство распредлений называется сопряжённым априорным распределением к функции правдоподобия P(Data|θ) (conjugate prior).

4.1 Бета распределение

\[P(x; α, β) = \frac{x^{α-1}\times (1-x)^{β-1}}{B(α, β)}; 0 \leq x \leq 1; α, β > 0\]

Бета функция:

\[Β(α, β) = \frac{Γ(α)\times Γ(β)}{Γ(α+β)} = \frac{(α-1)!(β-1)!}{(α+β-1)!} \]

tibble(x = seq(0, 1, length.out = 51),
           density = dbeta(x = x, shape1 = 8, shape2 = 42)) %>% 
  ggplot(aes(x, density))+
  geom_point()+
  geom_line()+
  labs(title = "Бета распределение α = 8, β = 42")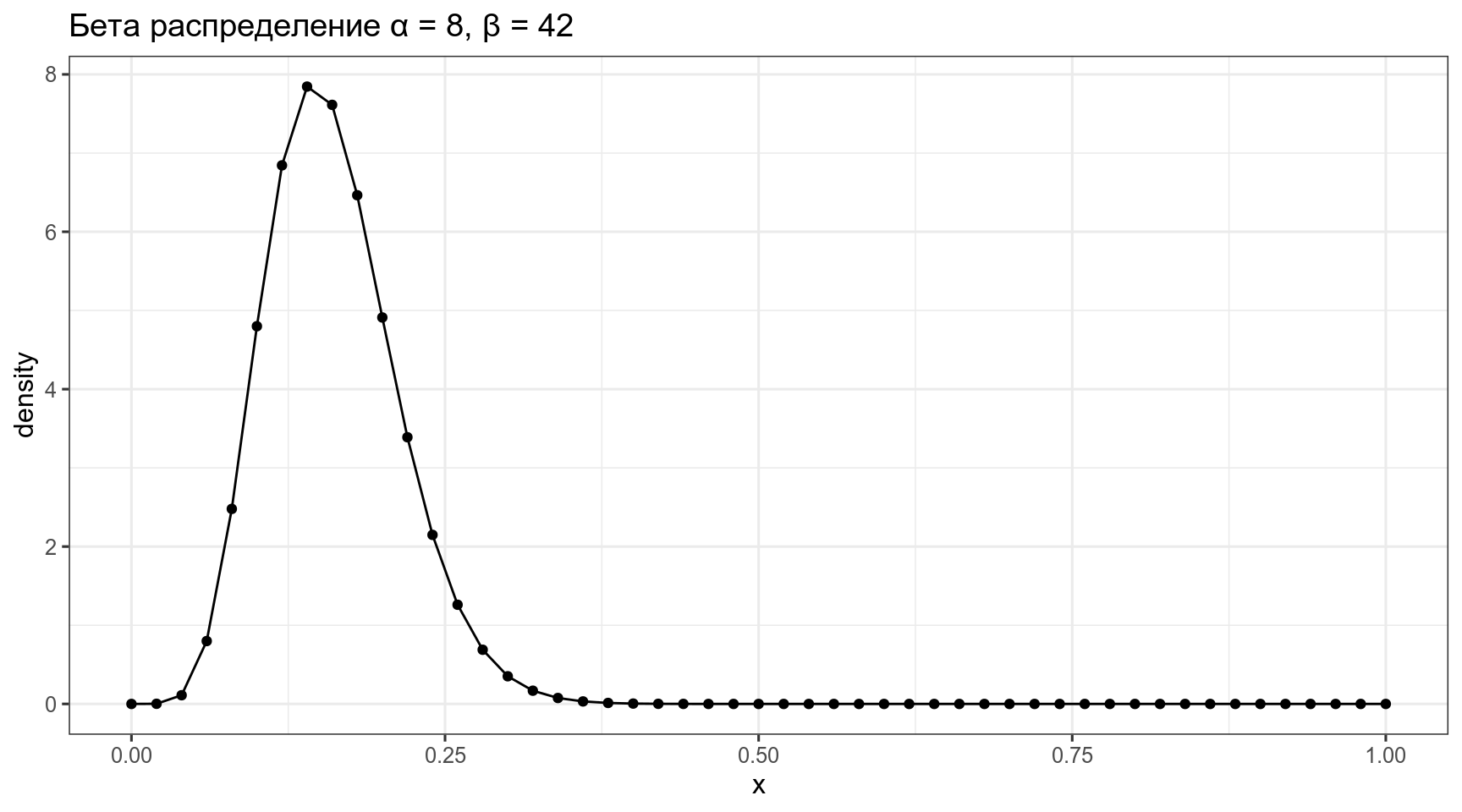

Можно поиграть с разными параметрами:

shiny::runGitHub("agricolamz/beta_distribution_shiny")

\[\mu = \frac{\alpha}{\alpha+\beta}\]

\[\sigma = \frac{\alpha\times\beta}{(\alpha+\beta)^2\times(\alpha+\beta+1)}\]

4.2 Нормальное распределение

4.3 Что еще почитать про распределения?

В интернете много ресурсов, но вот еще есть вот этот. А здесь можно найти соответсвия распределений и сопряжённым к ним априорных распределений.

5. Вероятность vs. функция правдободобия

Предположим что распределение количества согласных в языках мира можно описать нормальным распределением со средним 22 и стандартным отклонением 6:

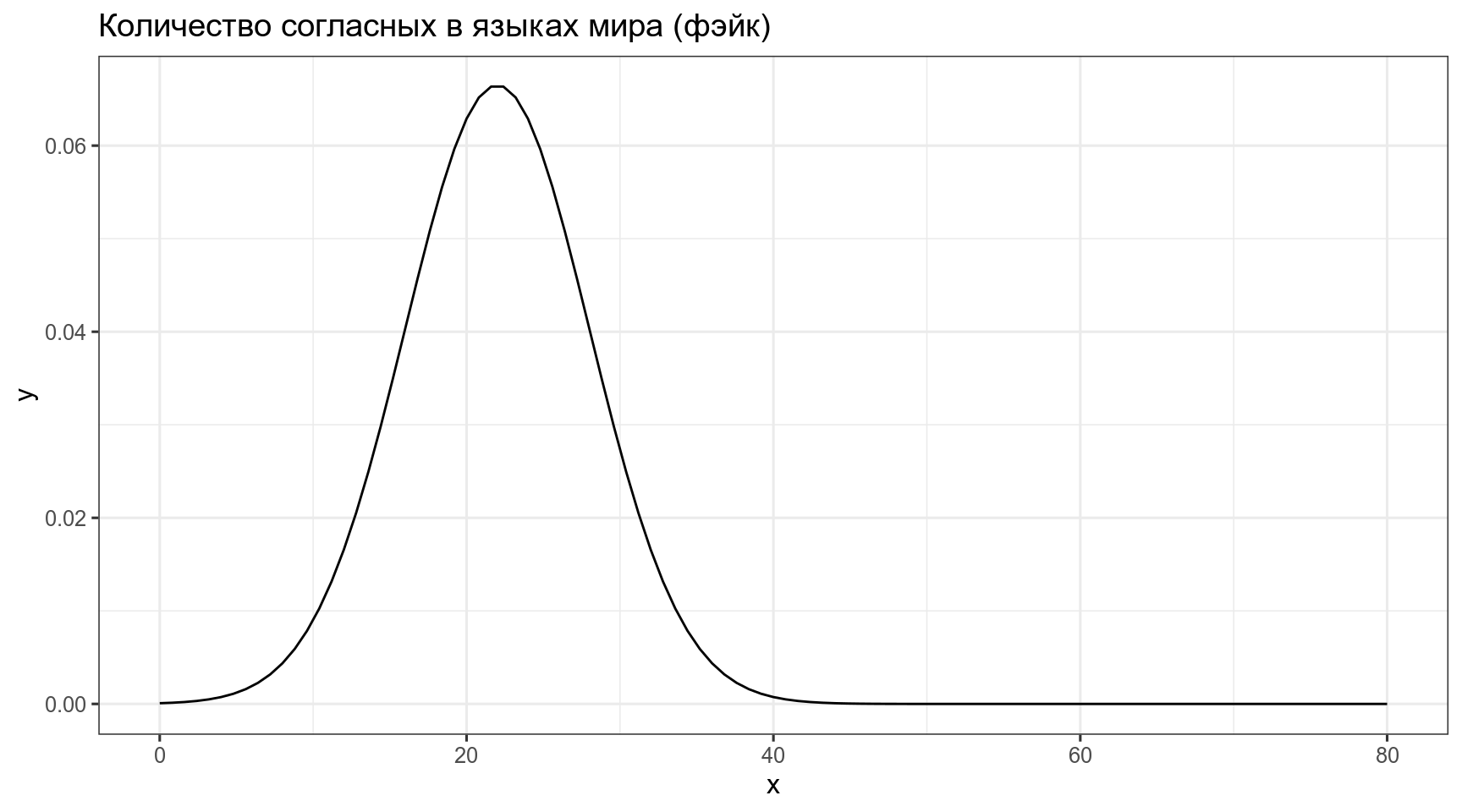
Тогда вероятность того, что в выбранных произвольно языках окажется от 23 до 32 согласных, равна интегралу нормального распределения в указанном промежутке:

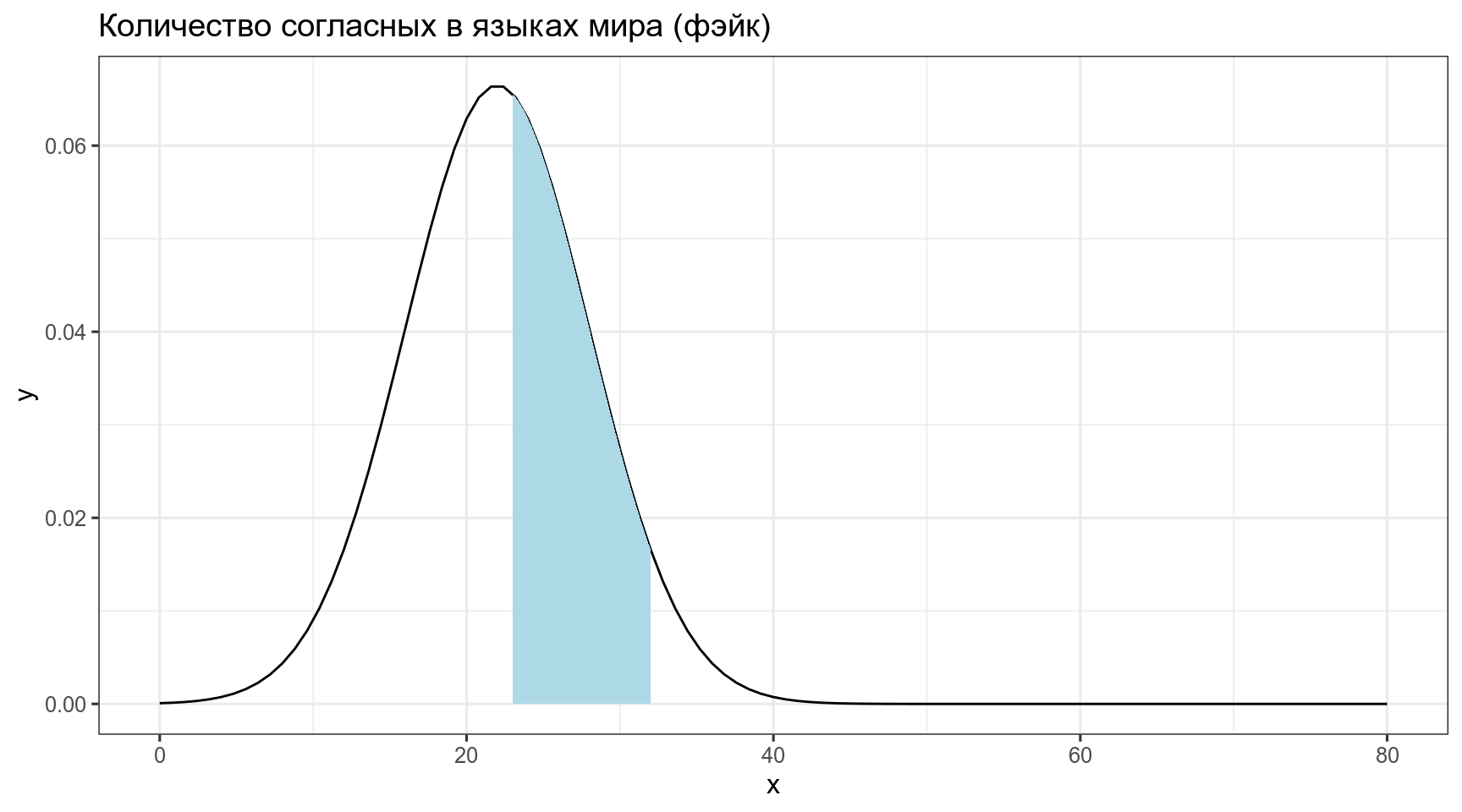
\[P\left(X \in (23,\, 32) | X \sim \mathcal{N}(\mu = 22,\, \sigma^{2}=6)\right) = ...\]

pnorm(32, mean = 22, sd = 6) - pnorm(23, mean = 22, sd = 6)

[1] 0.3860258

Когда мы говорим про функцию правдоподобия, мы нашли еще один язык в котором оказалось 33 согласных, и нас интересует, насколько правдоподобна функция нормального распределения со средним 22 и стандартным отклонением 6 при значении переменной 33. Это значение равно функции плотности:

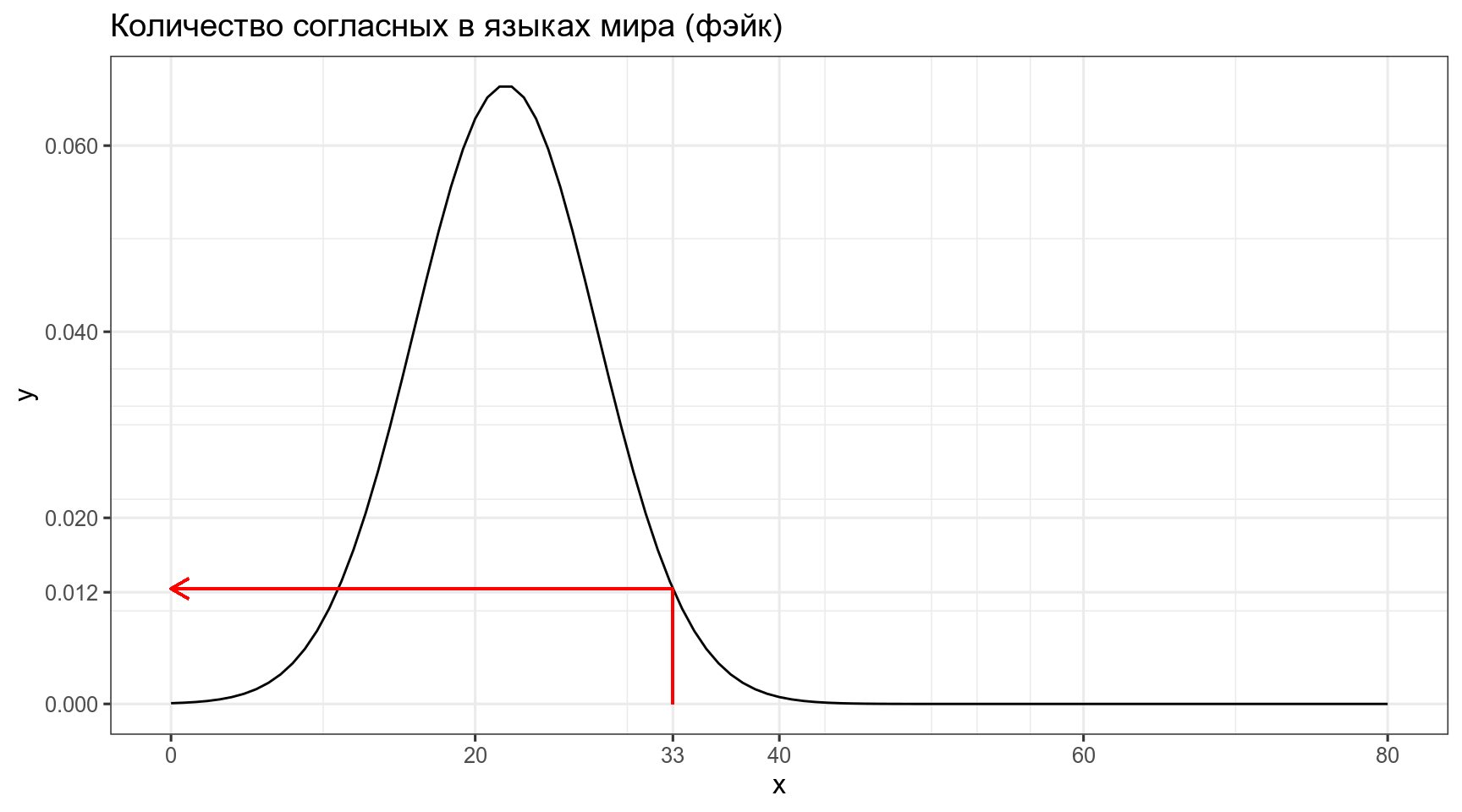
\[L\left(X \sim \mathcal{N}(\mu = 22,\, \sigma^{2}=6)|x = 33\right) = ...\]

dnorm(33, 22, 6)

[1] 0.01238519

В результате мы можем пострить график, на котором будет правдоподобие моделей с разными средними и фиксированным стандартным отклонением.

tibble(x = 0:80) %>% 
  ggplot(aes(x)) +
  stat_function(fun = function(x) dnorm(33, x, 6))+
  scale_x_continuous(breaks = c(0:4*20, 33))+
  labs(x = TeX("$\\mu$"),
       y = TeX("$L(N(\\mu,\\, \\sigma^{2}=6)|x = 33))$"),
       title = "Насколько правдоподобны модели с разными μ, если мы наблюдаем значение 33?")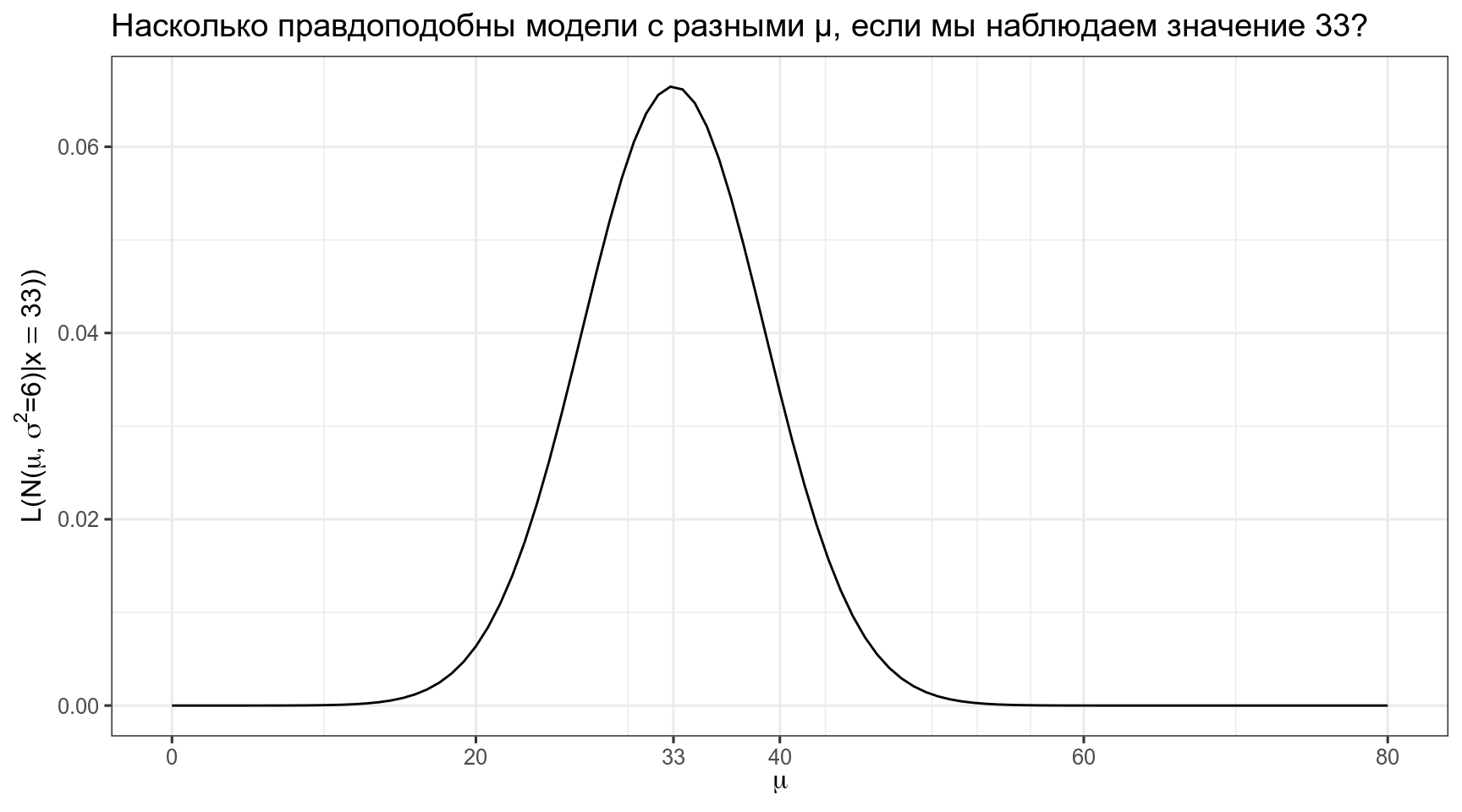

А что если у нас не одно наблюдение, а несколько? Например, мы наблюдаем языки с 33 и 26 согласными? События независимы друг от друга, значит, мы можем перемножить получаемые вероятности.

tibble(x = 0:80) %>% 
  ggplot(aes(x)) +
  stat_function(fun = function(x) dnorm(33, x, 6)*dnorm(26, x, 6))+
  scale_x_continuous(breaks = c(0:4*20, 33, 26))+
  labs(x = TeX("$\\mu$"),
       y = TeX("$L(N(\\mu,\\, \\sigma^{2}=6)|x = {33, 26}))$"),
       title = "Насколько правдоподобны модели с разными μ, если мы наблюдаем значения 26 и 33?")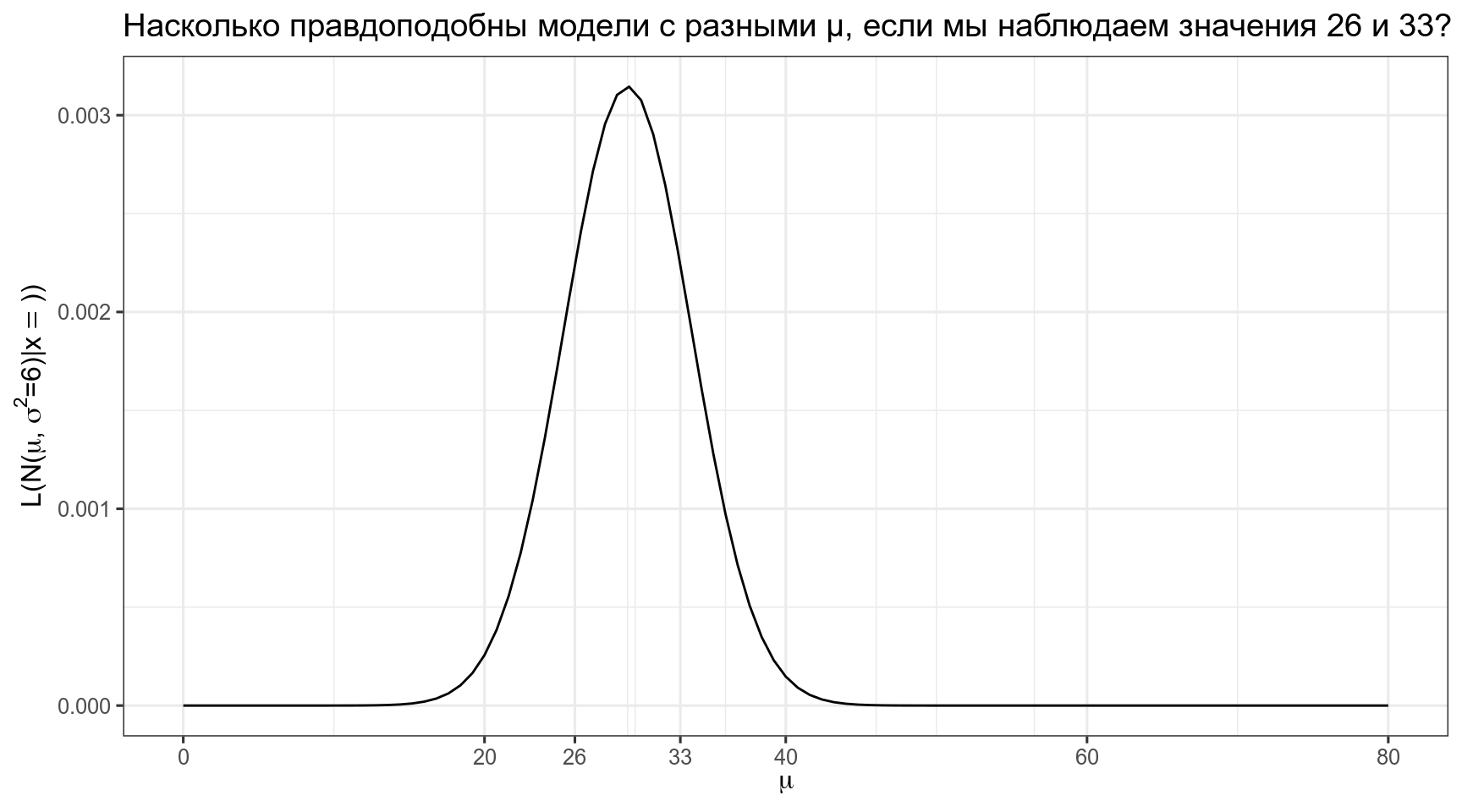

Самое важное:

вероятность — P(data|distribution)
правдоподобие — L(distribution|data)

Интеграл распределения вероятностей равен 1. Интеграл правдоподобия может быть не равен 1.

5.1

Посчитайте значение правдоподобия модели \(\mathcal{N}(\mu = 910,\, \sigma=150)\) для встроенного датасета Nile.

1. Распределения

Г. Мороз