library(tidyverse)

1. Рандомизаторы

1.1 Простой случай

В нашем курсе мы обсуждали несколько рандомизаторов (rnorm(), rbeta() и так далее). Но вернемся к более простому случаю. Сделаем одну выборку из множества, содержащего три элемента:

sample(x = 5:7)
[1] 7 5 6

По умолчанию он выдает множество равное количеству объектов в векторе.

sample(x = 5:7, size = 1)
[1] 5
sample(x = 5:7, size = 4)
Error in sample.int(length(x), size, replace, prob): cannot take a sample larger than the population when 'replace = FALSE'
sample(x = 5:7, size = 4, replace = TRUE)
[1] 7 6 7 7

Можно задавать вероятности, с которыми рандомизатор вынимает то или иное значение (по умолчанию все исходы равновероятны):

sample(x = 5:7, size = 10000, replace = TRUE) %>% 
  table() %>% 
  prop.table()
.
     5      6      7 
0.3345 0.3371 0.3284 
sample(x = 5:7, size = 10000, replace = TRUE, 
       prob = c(0.1, 0.3, 0.6)) %>% 
  table() %>% 
  prop.table()
.
     5      6      7 
0.0963 0.3093 0.5944

Записи идентичны:

sample(1:10)
 [1]  2 10  9  3  6  5  1  7  4  8
sample(10)
 [1]  7  4  6  9  5  1  8  3 10  2

Чтобы фиксировать рандомизатор следует использовать set.seed(). Посмотрите прекрасную работу Бена Мура на тему того, какие кто использует сиды на GitHub.

Иногда хочется, чтобы рандомизатор был одинаковый в R и Python, зачем и как это делать читайте в работе Гертьяна ван ден Бург: блог, гитхаб.

1.2 Сэмплирование из датафрейма

mtcars[sample(nrow(mtcars), 7),]
mtcars %>% 
  sample_n(7)
library(data.table)
mtcars[sample(.N, 7)]

2. Марковские цепи

Марковский процесс

  • конечное количество состояний
  • вероятность переходов из одного состояния в другое

Славная визуализация (спасибо за ссылку Марине Дубовой)

Возьмем наш датасет с погодой и отфильтруем только Сан Диего:

read_csv("https://raw.githubusercontent.com/agricolamz/2019_BayesDan_winter/master/datasets/weather.csv") %>% 
  select(city, date, events) %>% 
  filter(city == "San Diego") ->
  weather

weather %>% 
  ggplot(aes(date, events))+
  geom_point()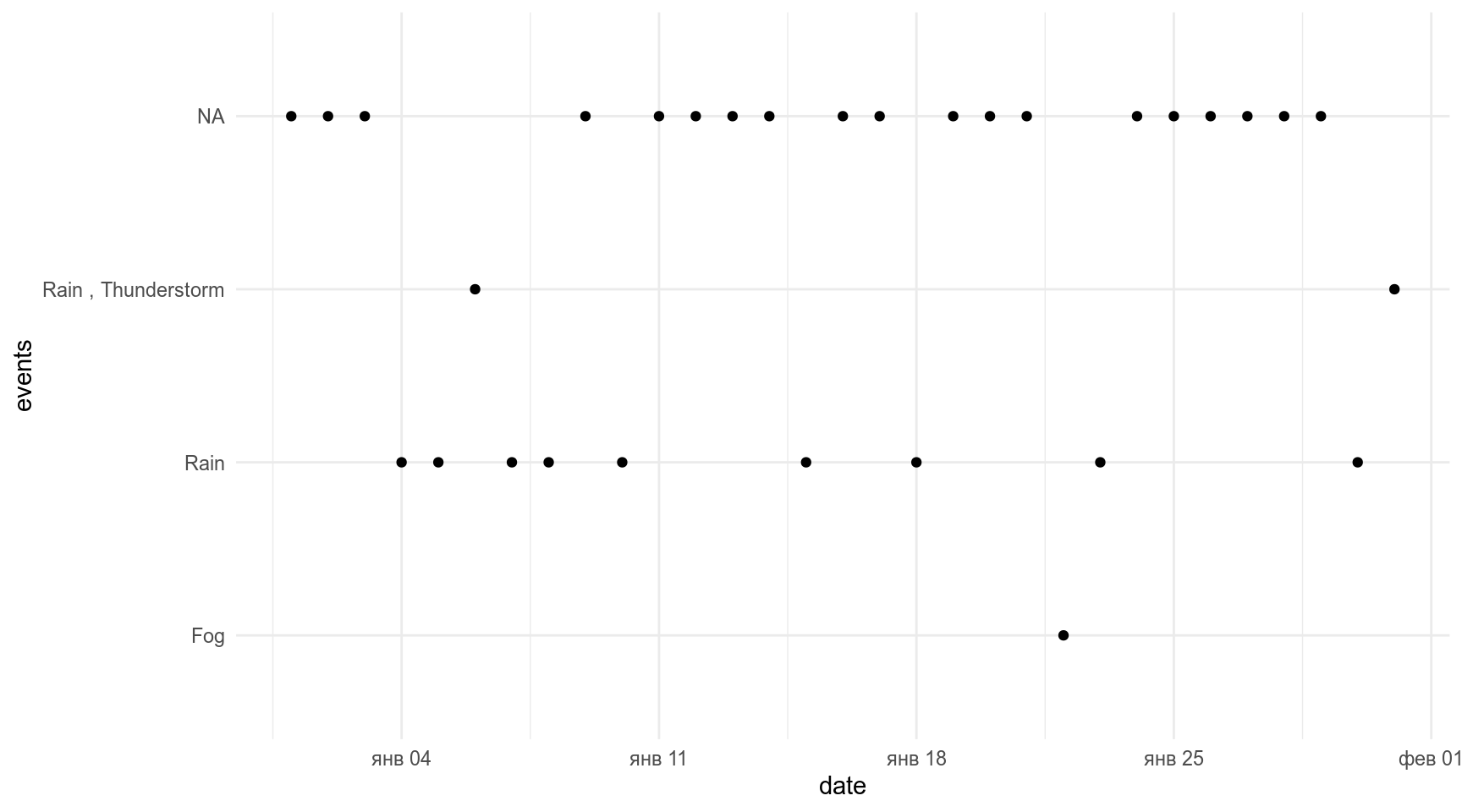

Давайте считать, что NA — это солнце.

weather %>% 
  mutate(events = ifelse(is.na(events), "Sun", events)) ->
  weather

weather%>% 
  ggplot(aes(date, events))+
  geom_point()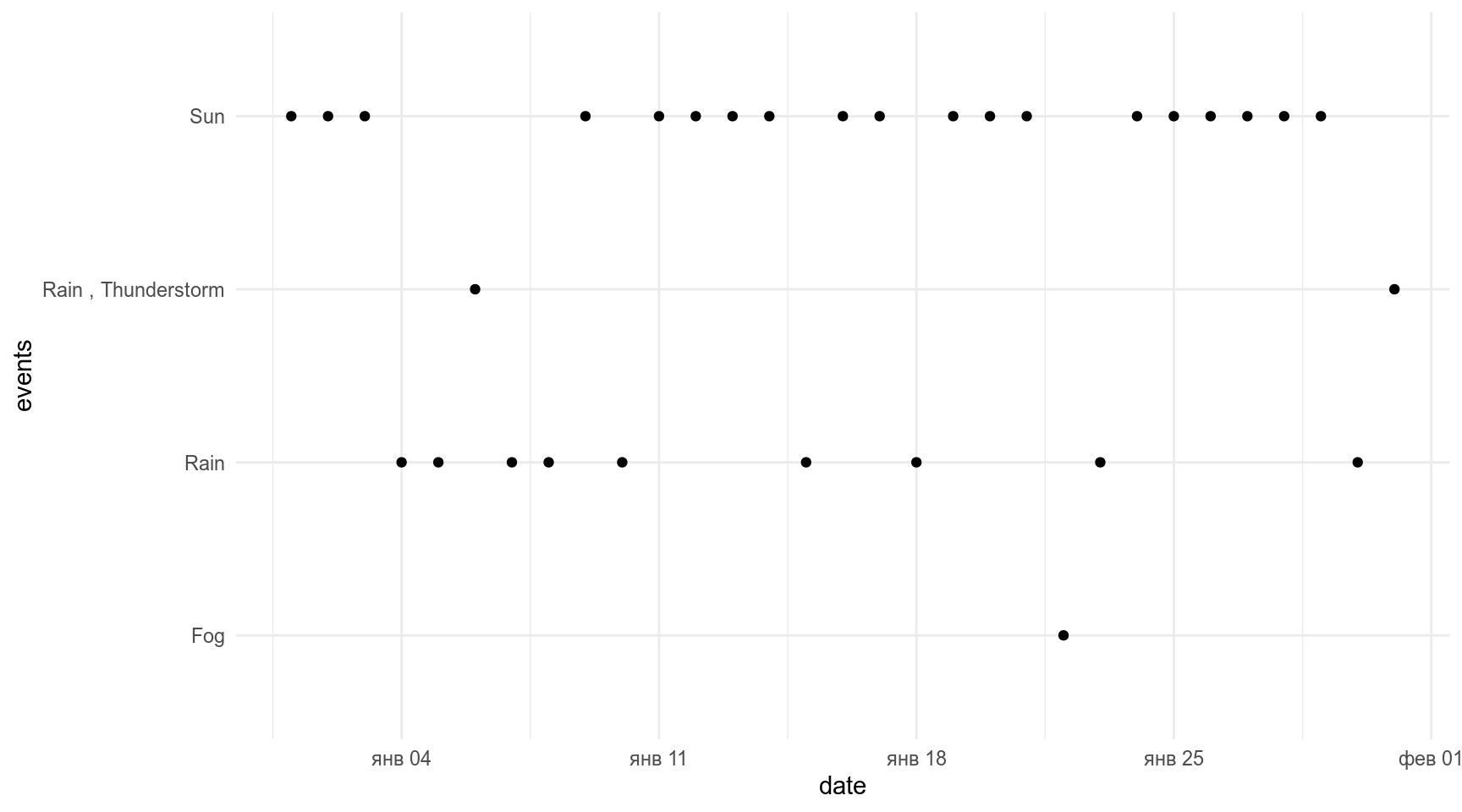

Визуализируем частоты разных погодных событий в Сан Диего:

weather %>% 
  count(events) %>% 
  mutate(events = reorder(factor(events), n)) %>% 
  ggplot(aes(events, n))+
  geom_col(fill = "lightblue")+
  coord_flip()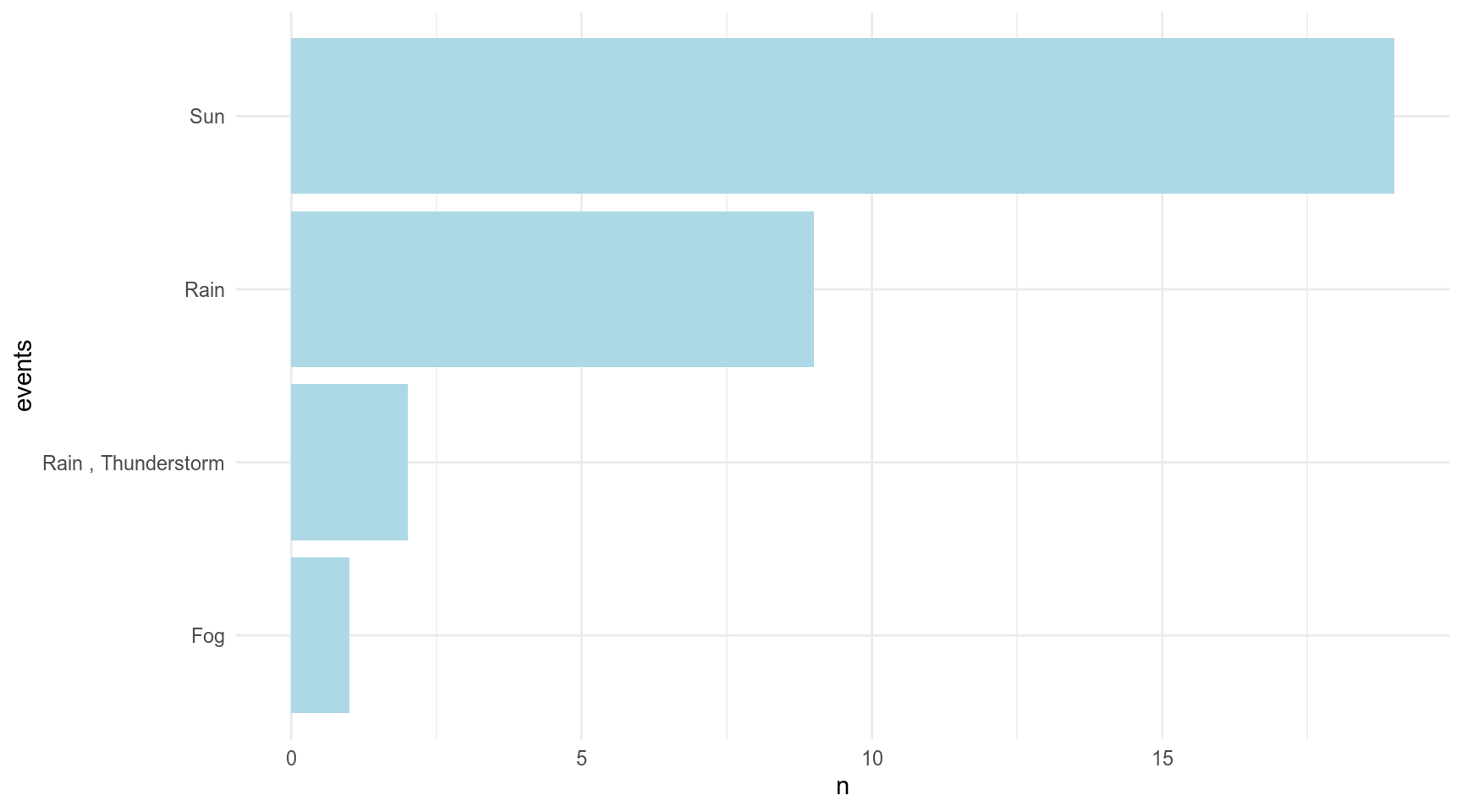

Визуализируем матрицу последовательных переходов разных погодных событий:

tibble(bigramma_1 = weather$events, 
           bigramma_2 = lead(weather$events, 1)) %>% 
  table() %>% 
  prop.table() %>% 
  as.data.frame() %>% 
  ggplot(aes(bigramma_1, bigramma_2, size = Freq, fill = Freq))+
  geom_raster()+
  geom_point()+
  scale_fill_gradient(low="grey95", high="red")+
  labs(title = 'Матрица переходов погодных событий в Сан Диего в январе')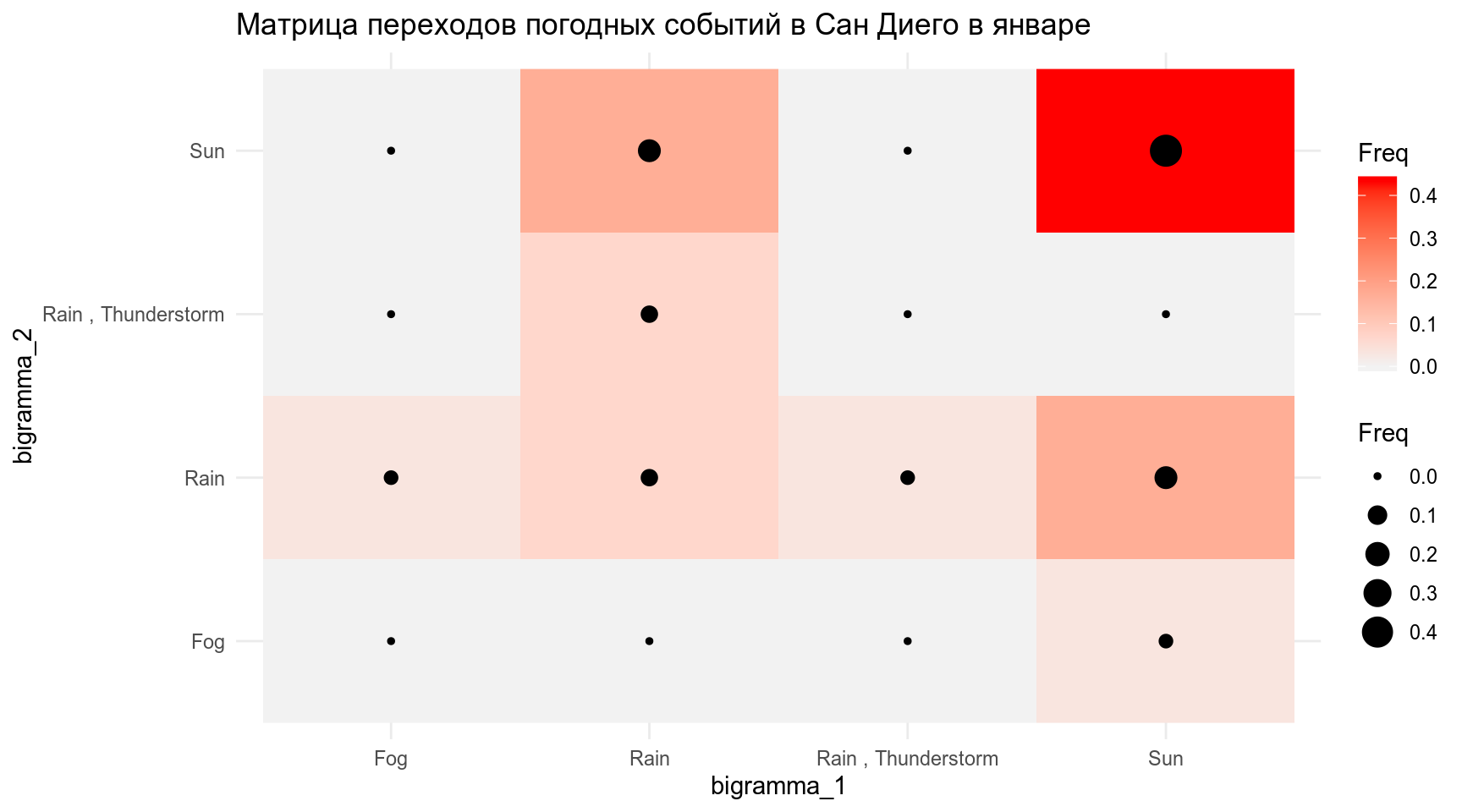

Сделаем марковскую цепь и визуализируем ее граф:

library(markovchain)
our_mc <- markovchainFit(weather$events)
our_mc$estimate
MLE Fit 
 A  4 - dimensional discrete Markov Chain defined by the following states: 
 Fog, Rain, Rain , Thunderstorm, Sun 
 The transition matrix  (by rows)  is defined as follows: 
                           Fog      Rain Rain , Thunderstorm       Sun
Fog                 0.00000000 1.0000000           0.0000000 0.0000000
Rain                0.00000000 0.2222222           0.2222222 0.5555556
Rain , Thunderstorm 0.00000000 1.0000000           0.0000000 0.0000000
Sun                 0.05263158 0.2631579           0.0000000 0.6842105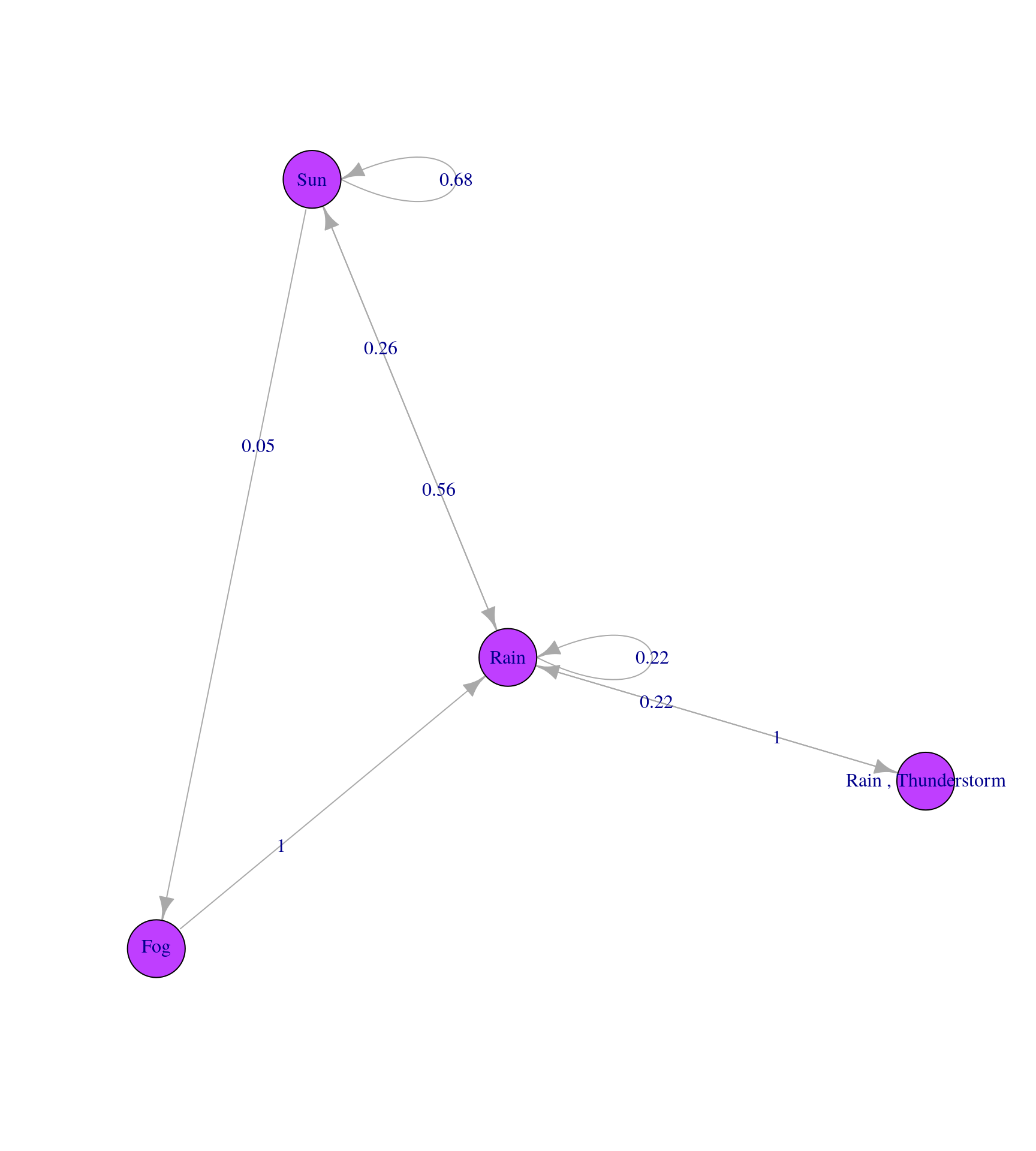
plot(our_mc$estimate)

Теперь мы можем предсказать наше следующее состояние \(t_2\) перемножив матрицу начального состояния \(t_1\) (\(1 \times 4\)) на матрицу переходов (\(4 \times 4\)).

\[t_2 = t_1 \times \text{transitional matrix}\]

Предположим, что наше начальное состояние — это дождь Rain:

t_1 <- matrix(c(0, 1, 0, 0), nrow = 1)
t_1 * our_mc$estimate # это особая звездочка из пакета markovchain
     Fog      Rain Rain , Thunderstorm       Sun
[1,]   0 0.2222222           0.2222222 0.5555556

Понятное дело состояние \(t_3\) это обычное произведение состояния \(t_2\) и матрицы переходов:

\[t_3 = t_2 \times \text{transitional matrix} = t_1 \times \text{transitional matrix} \times \text{transitional matrix} = t_1 \times \text{transitional matrix}^2\]

Используя полученную модель можно вычислите вероятность каждого из погодных событий на 7-ой день после дождя.

t_1 * our_mc$estimate ^ 7 # это особые звездочка и крышечка из пакета markovchain
            Fog     Rain Rain , Thunderstorm       Sun
[1,] 0.03005657 0.324639          0.07273401 0.5725704

Вообще-то, часто так бывает, что цепь сходиться на каком-то состоянии (состояние эквилибриум из домашнего задания) и дальше не изменяется. Давайте Визуализируем 40 состояний цепи, если начальное состояние — дождь.

df <- as.data.frame(t_1)
colnames(df) <- sort(unique(weather$events))

sapply(2:40, function(x){
  df[x,] <<- as.data.frame(as.matrix(df[1,]) * (our_mc$estimate^(x-1)))
})
                    [,1]      [,2]       [,3]       [,4]       [,5]      
Fog                 0         0.02923977 0.02650388 0.03035072 0.0296548 
Rain                0.2222222 0.4178038  0.3039872  0.3386555  0.3214342 
Rain , Thunderstorm 0.2222222 0.04938272 0.09284528 0.0675527  0.07525677
Sun                 0.5555556 0.5035737  0.5766637  0.5634411  0.5736543 
                    [,6]       [,7]       [,8]       [,9]       [,10]     
Fog                 0.03019233 0.03005657 0.03013529 0.03011125 0.03012316
Rain                0.327303   0.324639   0.325609   0.3251911  0.3253493 
Rain , Thunderstorm 0.07142982 0.07273401 0.072142   0.07235756 0.07226468
Sun                 0.5710748  0.5725704  0.5721137  0.5723401  0.5722628 
                    [,11]      [,12]      [,13]      [,14]      [,15]     
Fog                 0.0301191  0.03012094 0.03012027 0.03012056 0.03012045
Rain                0.3252832  0.3253088  0.3252983  0.3253024  0.3253007 
Rain , Thunderstorm 0.07229985 0.07228515 0.07229084 0.07228851 0.07228942
Sun                 0.5722979  0.5722851  0.5722906  0.5722885  0.5722894 
                    [,16]      [,17]      [,18]      [,19]      [,20]     
Fog                 0.03012049 0.03012048 0.03012048 0.03012048 0.03012048
Rain                0.3253014  0.3253011  0.3253012  0.3253012  0.3253012 
Rain , Thunderstorm 0.07228905 0.0722892  0.07228914 0.07228916 0.07228915
Sun                 0.5722891  0.5722892  0.5722891  0.5722892  0.5722892 
                    [,21]      [,22]      [,23]      [,24]      [,25]     
Fog                 0.03012048 0.03012048 0.03012048 0.03012048 0.03012048
Rain                0.3253012  0.3253012  0.3253012  0.3253012  0.3253012 
Rain , Thunderstorm 0.07228916 0.07228916 0.07228916 0.07228916 0.07228916
Sun                 0.5722892  0.5722892  0.5722892  0.5722892  0.5722892 
                    [,26]      [,27]      [,28]      [,29]      [,30]     
Fog                 0.03012048 0.03012048 0.03012048 0.03012048 0.03012048
Rain                0.3253012  0.3253012  0.3253012  0.3253012  0.3253012 
Rain , Thunderstorm 0.07228916 0.07228916 0.07228916 0.07228916 0.07228916
Sun                 0.5722892  0.5722892  0.5722892  0.5722892  0.5722892 
                    [,31]      [,32]      [,33]      [,34]      [,35]     
Fog                 0.03012048 0.03012048 0.03012048 0.03012048 0.03012048
Rain                0.3253012  0.3253012  0.3253012  0.3253012  0.3253012 
Rain , Thunderstorm 0.07228916 0.07228916 0.07228916 0.07228916 0.07228916
Sun                 0.5722892  0.5722892  0.5722892  0.5722892  0.5722892 
                    [,36]      [,37]      [,38]      [,39]     
Fog                 0.03012048 0.03012048 0.03012048 0.03012048
Rain                0.3253012  0.3253012  0.3253012  0.3253012 
Rain , Thunderstorm 0.07228916 0.07228916 0.07228916 0.07228916
Sun                 0.5722892  0.5722892  0.5722892  0.5722892 
df %>% 
  mutate(stage = 1:40) %>% 
  gather(events, value, Fog:Sun) %>% 
  ggplot(aes(stage, value, color = events))+
  geom_line(show.legend = FALSE)+
  directlabels::geom_dl(aes(label = events), method = "last.qp")+
  labs(title = 'Марковская цепь погодных событий в Сан Диего в январе',
       caption = "начальное состояние --- дождь (Rain)")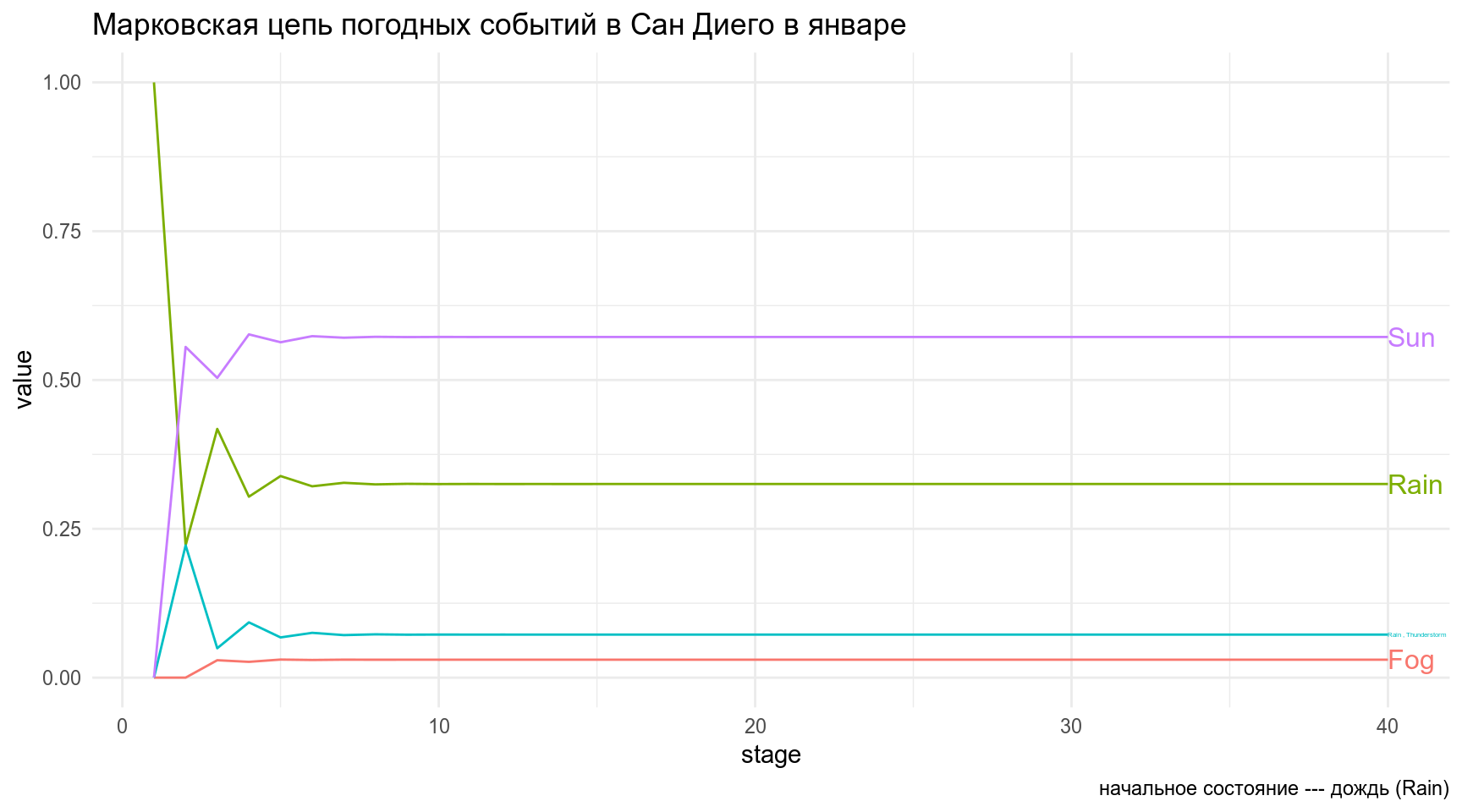

И люди вообще-то научились вычислять такие вещи на основании цепи:

steadyStates(our_mc$estimate)
            Fog      Rain Rain , Thunderstorm       Sun
[1,] 0.03012048 0.3253012          0.07228916 0.5722892

Скачайте датасет, который содержит роман “По эту сторону рая” Ф. С. Фицджеральда:

  • token — слово
  • POS — часть речи, полученная на основе английской модели UDPIPE.

Визуализируйте частоты частей речи в романе: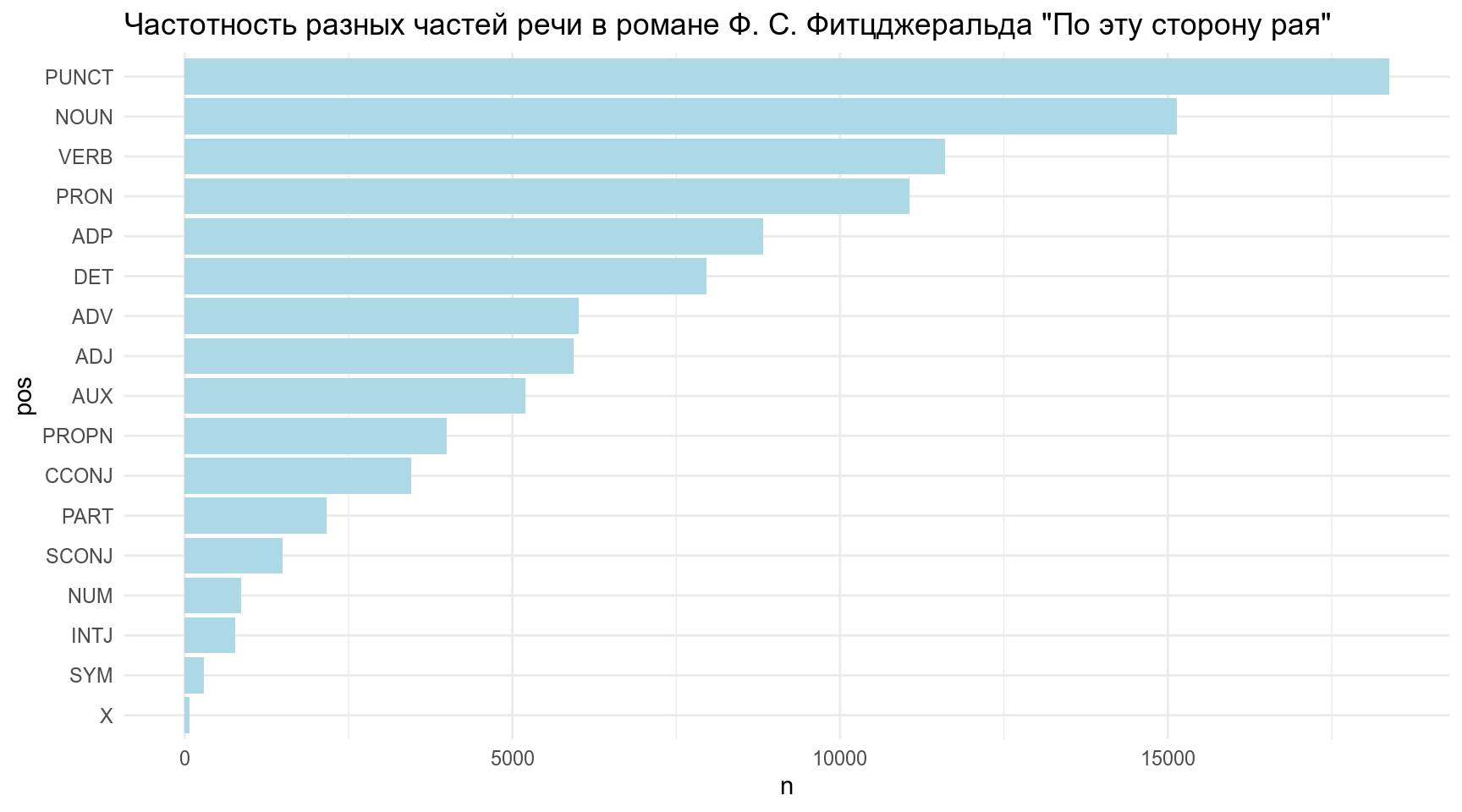

Визуализируйте матрицу последовательных переходов частей речи:

Сделайте марковскую цепь и визуализируйте ее граф:

Используя полученную модель, вычислите вероятность встретить после артикля (DET) прилагательное (ADJ) (с точностью до трех знаков после запятой).


Используя полученную модель, вычислите вероятность встретить после артикля прилагательное в четвертом по счету слове (с точностью до трех знаков после запятой).

t_1 * our_mc$estimate ^ 4 # t_5 using markovchain package
            ADJ        ADP        ADV        AUX      CCONJ       DET
[1,] 0.06364596 0.07437913 0.05648417 0.05594779 0.03150212 0.0760366
            INTJ      NOUN         NUM       PART      PRON      PROPN
[1,] 0.008021889 0.1565543 0.008617353 0.01814057 0.1067079 0.04168071
         PUNCT      SCONJ        SYM      VERB            X
[1,] 0.1700765 0.01359084 0.00284206 0.1150473 0.0007247423

Визуализируйте 40 состояний цепи, если начальное состояние — артикль (DET).

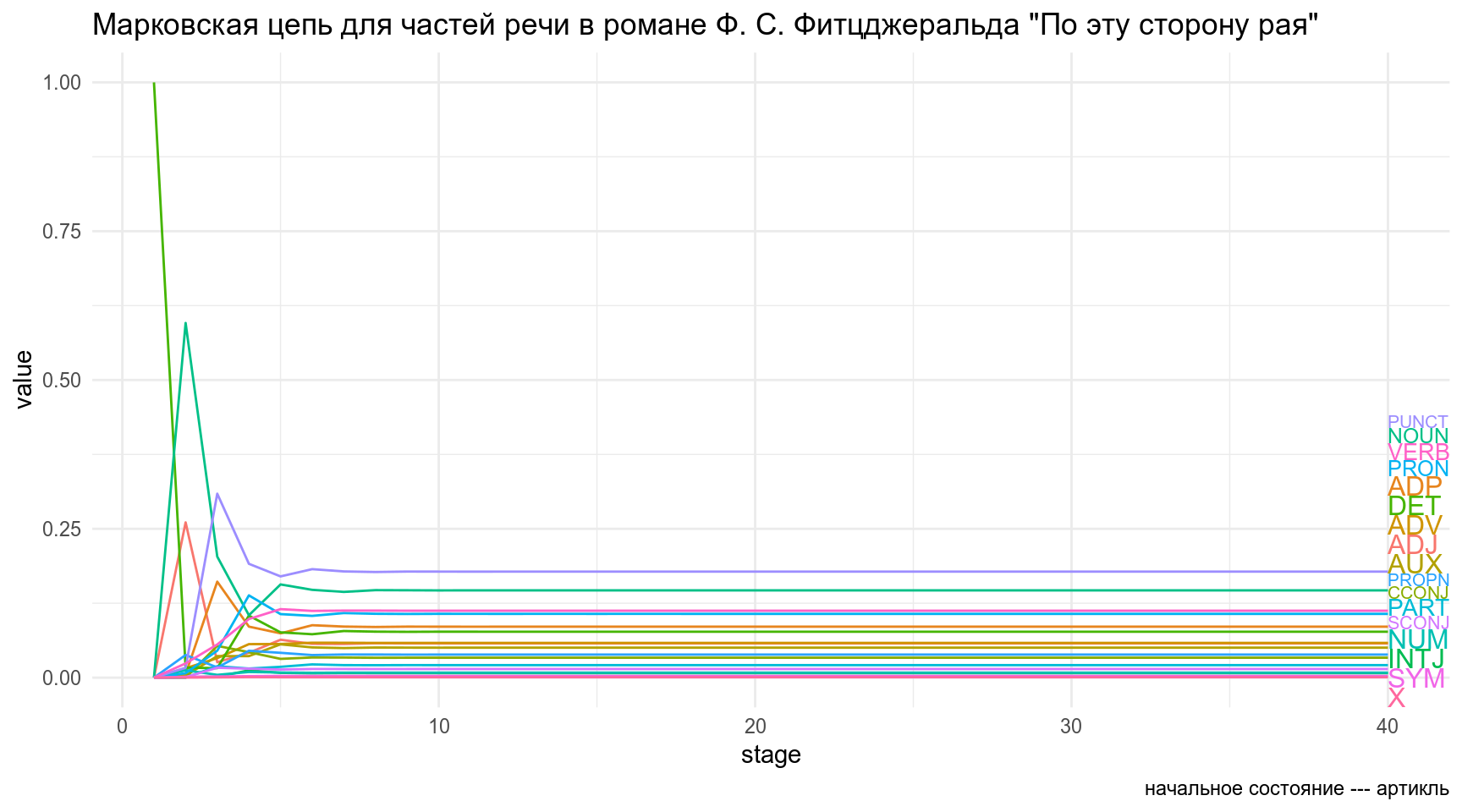
Посчитайте фиксированные состояния цепи. В ответе приведите значение для местоимения (с точностью до трех знаков после запятой).


3 Что дальше?

  • легко придумать обобщение этой логики на непрерывные данные
  • можно придумать вариант, когда мы пытаемся предсказать некоторые ненаблюдаемые вещи на основании наблюдаемых: например, погоду в Сан Диего на основании настроение вашего друга, которому вы каждый день звоните. Это называется скрытые марковские цепи.
  • MCMC (Markov Chain Monte Carlo)

3.1 Метод Монте-Карло

Группа методов изучения случайных процессов, которые базируются на:

  • возможности производить бесконечного количества случайных переменных
  • для известных или новых распределенийы

Представим себе, что у нас есть какой-то интеграл, который мы хотим посчитать. Например такой:

tibble(x = seq(0, 1, length.out = 1000)) %>% 
  ggplot(aes(x))+
  stat_function(fun = function(x){x^12-sin(x)+1}, geom = "area", fill = "lightblue")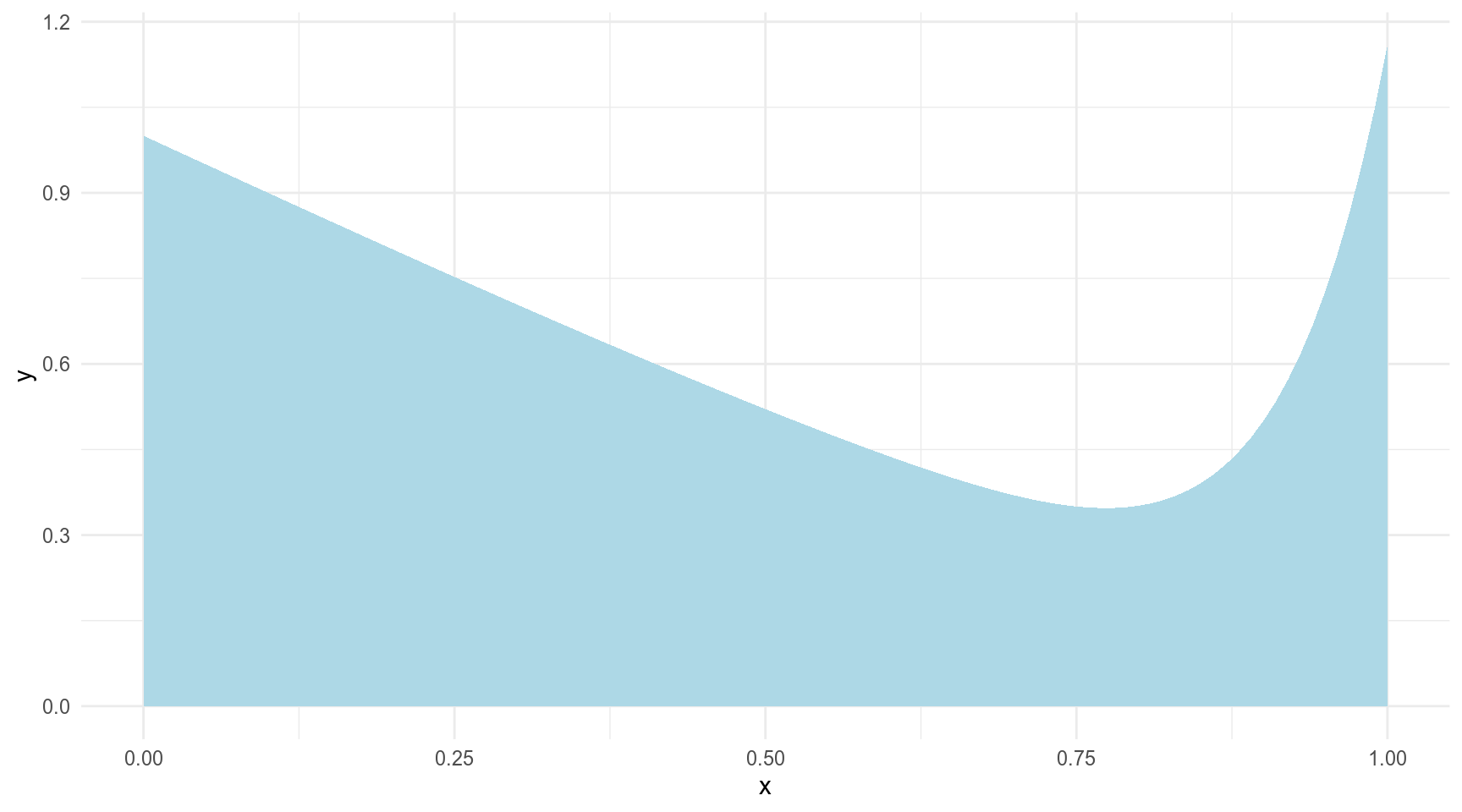

Мы можем насэмплировать точек из комбинации двух унимодальных распределений u(0, 1), и u(0, 1.2) и посмотреть, кто попадает в область, а кто нет:

set.seed(42)
tibble(x = runif(1e3, 0, 1), 
       y = runif(1e3, 0, 1.2),
       in_area = y < x^12-sin(x)+1) %>% 
  ggplot(aes(x, y))+
  stat_function(fun = function(x){x^12-sin(x)+1}, geom = "area", fill = "lightblue")+
  geom_point(aes(color = in_area), show.legend = FALSE)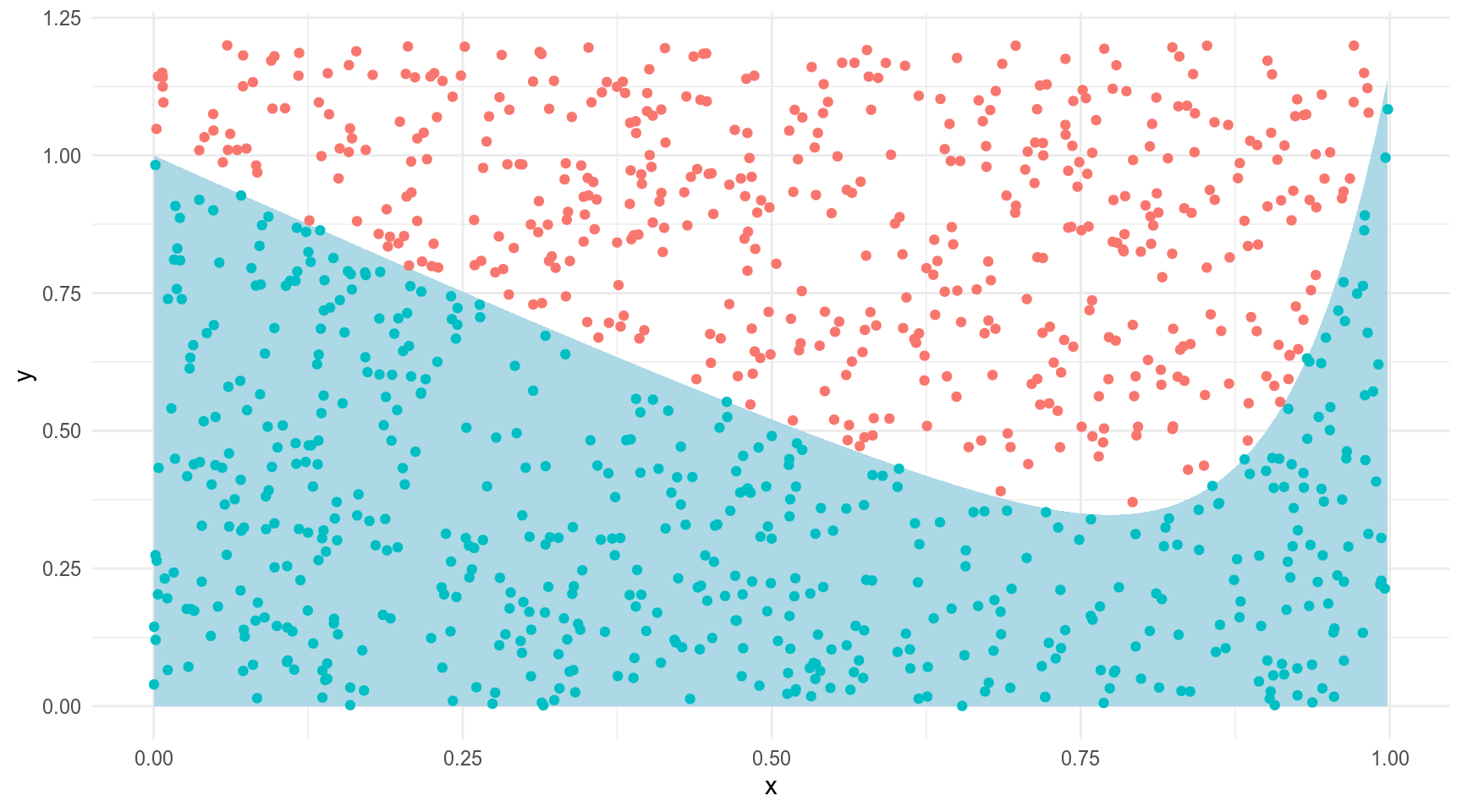

Сколько попало?

set.seed(42)
tibble(x = runif(1e3, 0, 1), 
       y = runif(1e3, 0, 1.2),
       in_area = y < x^12-sin(x)+1) %>% 
  count(in_area)
528/1000*1.2
[1] 0.6336
integrate(function(x){x^12-sin(x)+1}, 0, 1)
0.6172254 with absolute error < 6.9e-15

А если увеличить количество наблюдений?

set.seed(42)
tibble(x = runif(1e7, 0, 1), 
       y = runif(1e7, 0, 1.2),
       in_area = y < x^12-sin(x)+1) %>% 
  count(in_area)
5143667/10000000*1.2
[1] 0.61724
integrate(function(x){x^12-sin(x)+1}, 0, 1)
0.6172254 with absolute error < 6.9e-15

Теперь ваш черед: оцените интеграл функции \(cos(3x)+arctan(7x)\) на промежутке от [0, 5] используйте (максимумальный y = 3) set.seed(42) и миллион итераций рандомизатора. В ответе приведите разницу между получившейся оценкой и реальным интегралом (до третьего знака после запятой):


MCMC (Markov Chain Monte Carlo)

Вот пример, в интеренете есть еще куча.




© Г. Мороз 2019 с помощью RMarkdown. Исходный код на GitHub