9 Ограничения на применение регрессии

Некоторые думают, что линейная регрессия решит все их проблемы (по крайней мере те из них, которые связаны с предсказанием какой-то числовой переменной). Это так. Но нужно быть осторожным — у регрессии есть свои ограничения на применение.

9.1 Введение

Ссылка на RMD с обсуждением.

9.1.1 Библиотеки

library(tidyverse)

9.1.2 Lexical Decision Task data

Dataset and description from Rling package by Natalia Levshina. This data set contains 100 randomly selected words from the English Lexicon Project data (Balota et al. 2007), their lengths, mean reaction times and corpus frequencies.

ldt <- read_csv("https://goo.gl/ToxfU6")
ldt

9.2 Нелинейность взаимосвязи

Давайте посмотрим на простой график:

ldt %>% 
  ggplot(aes(Mean_RT, Freq))+
  geom_point()+
  theme_bw()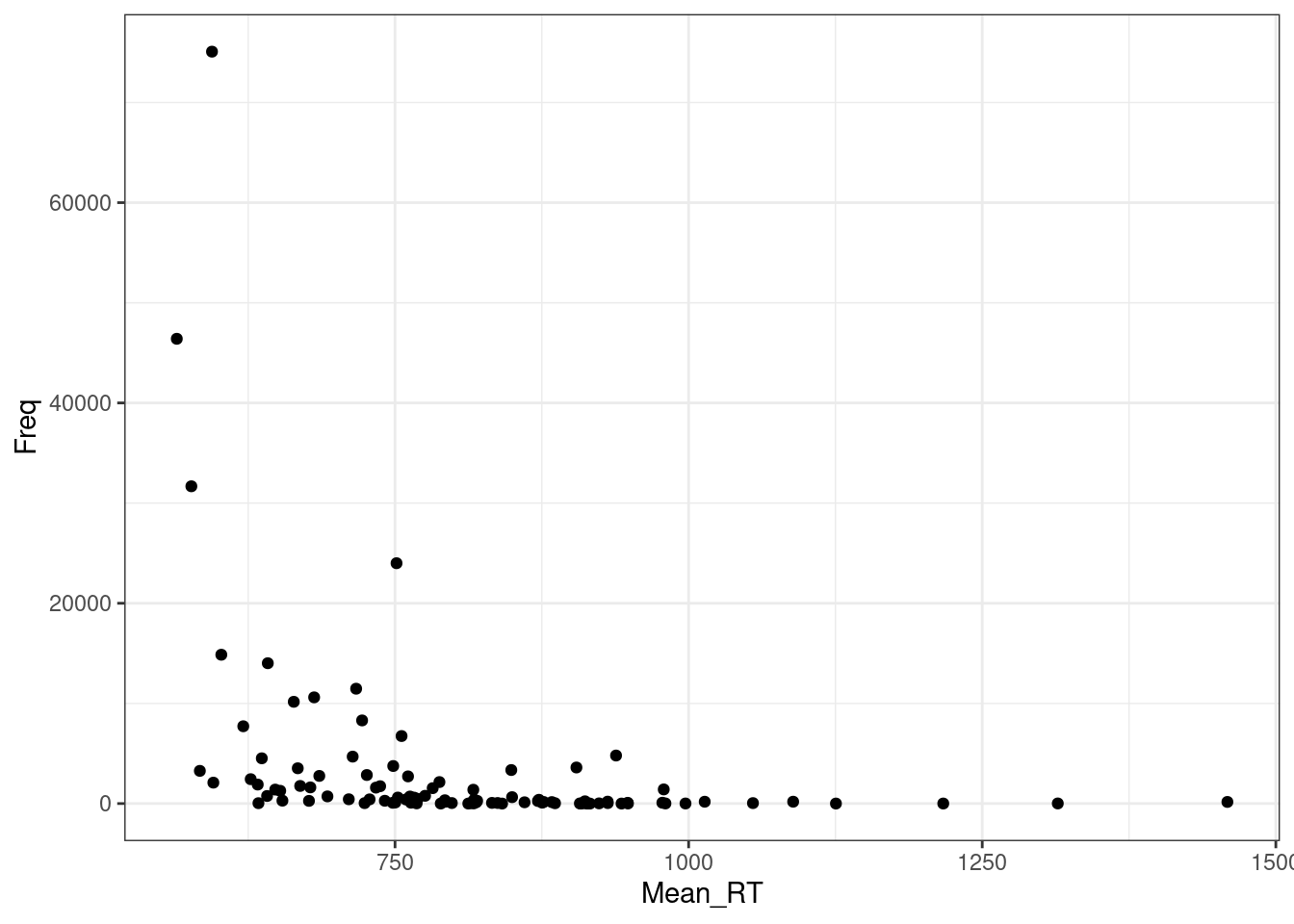

Регрессия на таких данных будет супер неиформативна:

ldt %>% 
  ggplot(aes(Mean_RT, Freq))+
  geom_point()+
  geom_smooth(method = "lm")+
  theme_bw()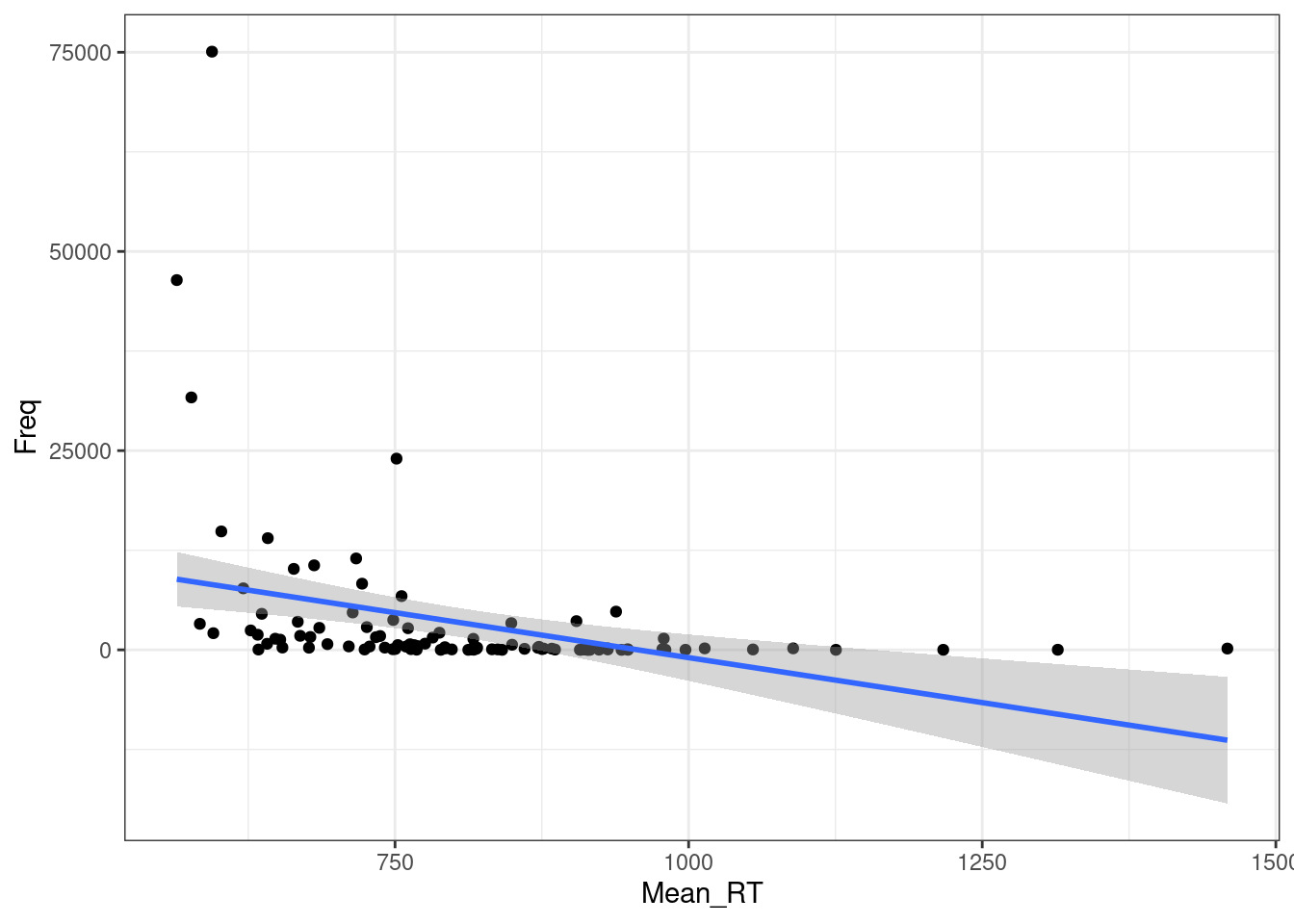

m1 <- summary(lm(Mean_RT~Freq, data = ldt))
m1

Call:
lm(formula = Mean_RT ~ Freq, data = ldt)

Residuals:
    Min      1Q  Median      3Q     Max 
-224.93  -85.42  -30.52   81.90  632.66 

Coefficients:
              Estimate Std. Error t value             Pr(>|t|)    
(Intercept) 826.998242  15.229783  54.301 < 0.0000000000000002 ***
Freq         -0.005595   0.001486  -3.765             0.000284 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 143.9 on 98 degrees of freedom
Multiple R-squared:  0.1264,    Adjusted R-squared:  0.1174 
F-statistic: 14.17 on 1 and 98 DF,  p-value: 0.0002843

9.2.1 Логарифмирование

ldt %>% 
  ggplot(aes(Mean_RT, log(Freq)))+
  geom_point()+
  geom_smooth(method = "lm")+
  theme_bw()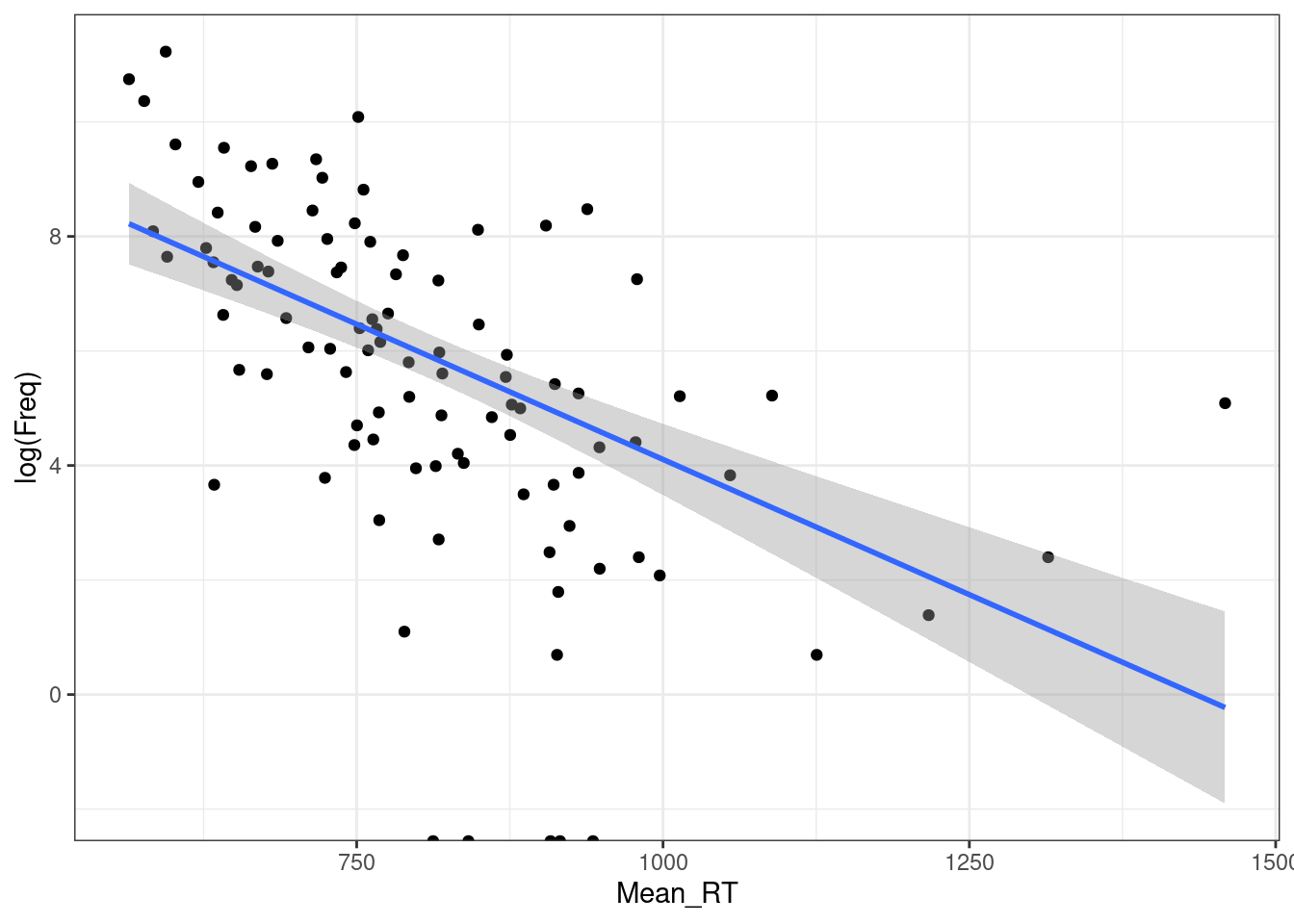

ldt %>% 
  ggplot(aes(Mean_RT, log(Freq+1)))+
  geom_point()+
  geom_smooth(method = "lm")+
  theme_bw()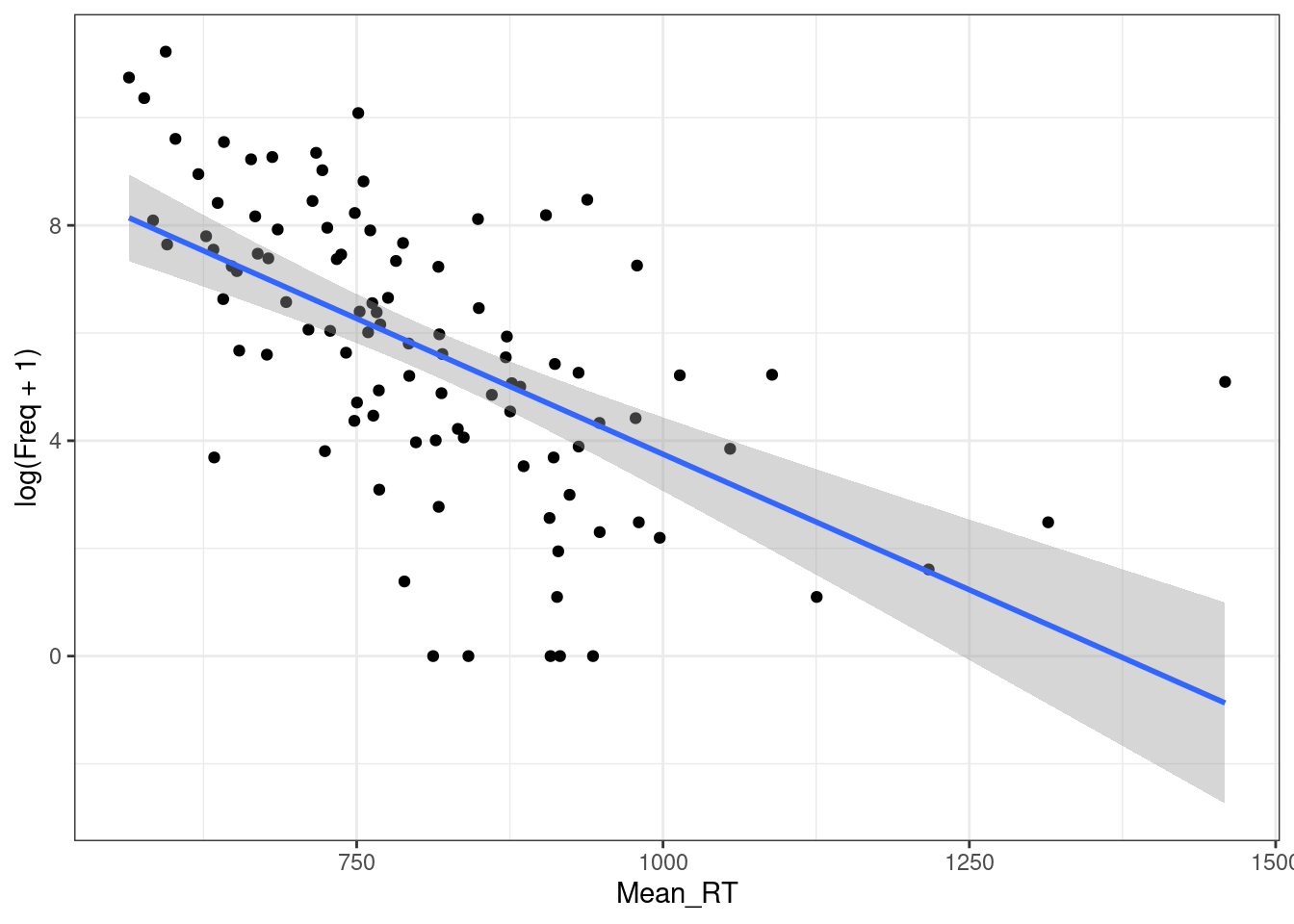

m2 <- summary(lm(Mean_RT~log(Freq+1), data = ldt))
m2

Call:
lm(formula = Mean_RT ~ log(Freq + 1), data = ldt)

Residuals:
    Min      1Q  Median      3Q     Max 
-242.36  -76.66  -17.49   48.64  630.49 

Coefficients:
              Estimate Std. Error t value             Pr(>|t|)    
(Intercept)    1001.60      29.79  33.627 < 0.0000000000000002 ***
log(Freq + 1)   -34.03       4.76  -7.149       0.000000000158 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 124.8 on 98 degrees of freedom
Multiple R-squared:  0.3428,    Adjusted R-squared:  0.3361 
F-statistic: 51.11 on 1 and 98 DF,  p-value: 0.0000000001576

m1$adj.r.squared

[1] 0.1174405

m2$adj.r.squared

[1] 0.336078

Отлогорифмировать можно и другую переменную.

ldt %>% 
  ggplot(aes(log(Mean_RT), log(Freq  + 1)))+
  geom_point()+
  geom_smooth(method = "lm")+
  theme_bw()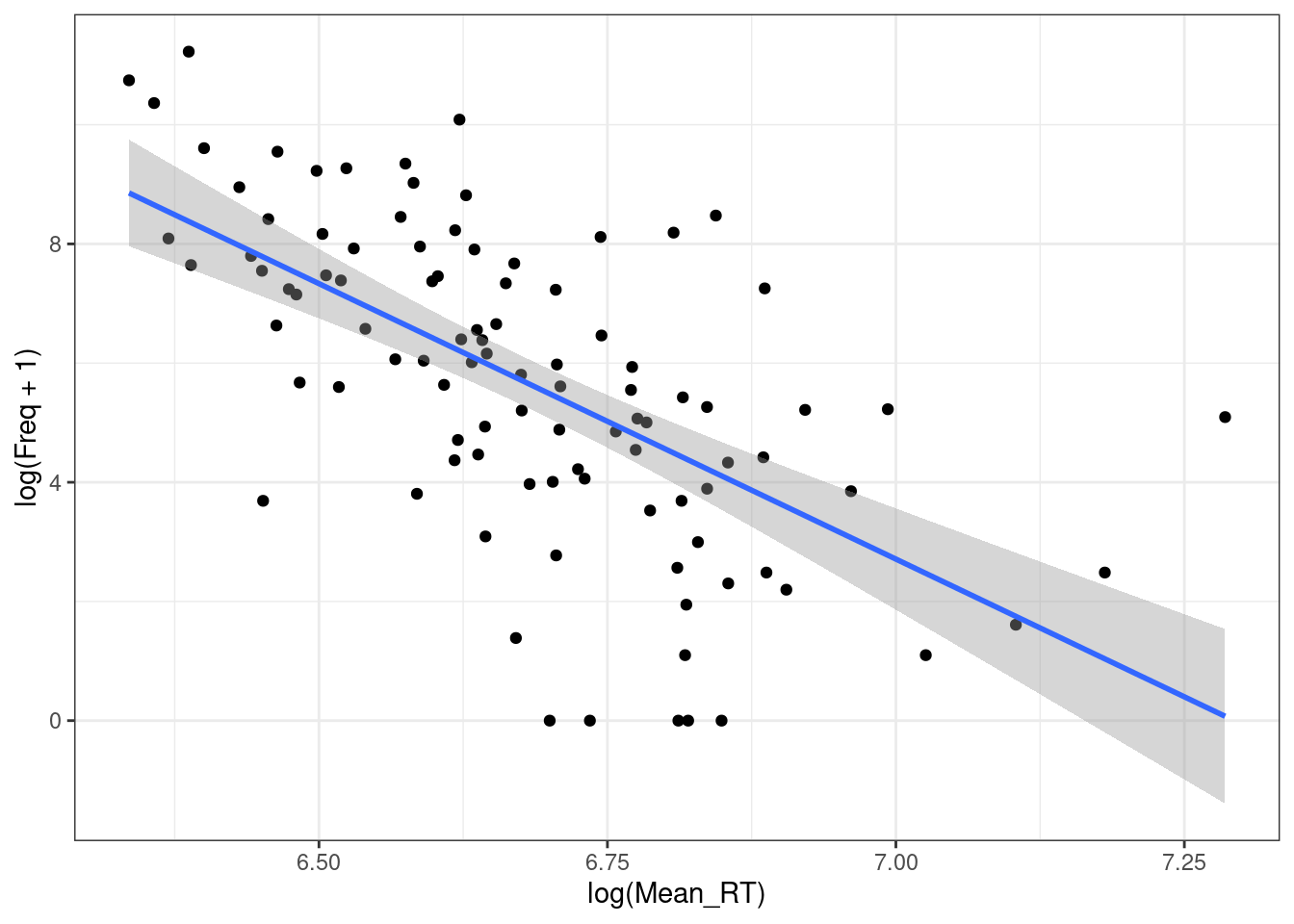

m3 <- summary(lm(log(Mean_RT)~log(Freq+1), data = ldt))
m1$adj.r.squared

[1] 0.1174405

m2$adj.r.squared

[1] 0.336078

m3$adj.r.squared

[1] 0.3838649

Как интерпретировать полученную регрессию с двумя отлогорифмированными значениями?

В обычной линейной регресии мы узнаем отношения между \(x\) и \(y\): \[y_i = \beta_0+\beta_1\times x_i\]

Как изменится \(y_j\), если мы увеличем \(x_i + 1 = x_j\)? \[y_j = \beta_0+\beta_1\times x_j\]

\[y_j - y_i = \beta_0+\beta_1\times x_j - (\beta_0+\beta_1\times x_i) = \beta_1(x_j - x_i)\]

Т. е. \(y\) увеличится на \(\beta_1\) , если \(x\) увеличится на 1. Что же будет с логарифмированными переменными? Как изменится \(y_j\), если мы увеличем \(x_i + 1 = x_j\)?

\[\log(y_j) - \log(y_i) = \beta_1\times (\log(x_j) - \log(x_i))\]

\[\log\left(\frac{y_j}{y_i}\right) = \beta_1\times \log\left(\frac{x_j}{x_i}\right) = \log\left(\left(\frac{x_j}{x_i}\right) ^ {\beta_1}\right)\]

\[\frac{y_j}{y_i}= \left(\frac{x_j}{x_i}\right) ^ {\beta_1}\]

Т. е. \(y\) увеличится на \(\beta_1\) процентов, если \(x\) увеличится на 1 процент.

Логарифмирование — не единственный вид траснформации:

• трансформация Тьюки

shiny::runGitHub("agricolamz/tukey_transform")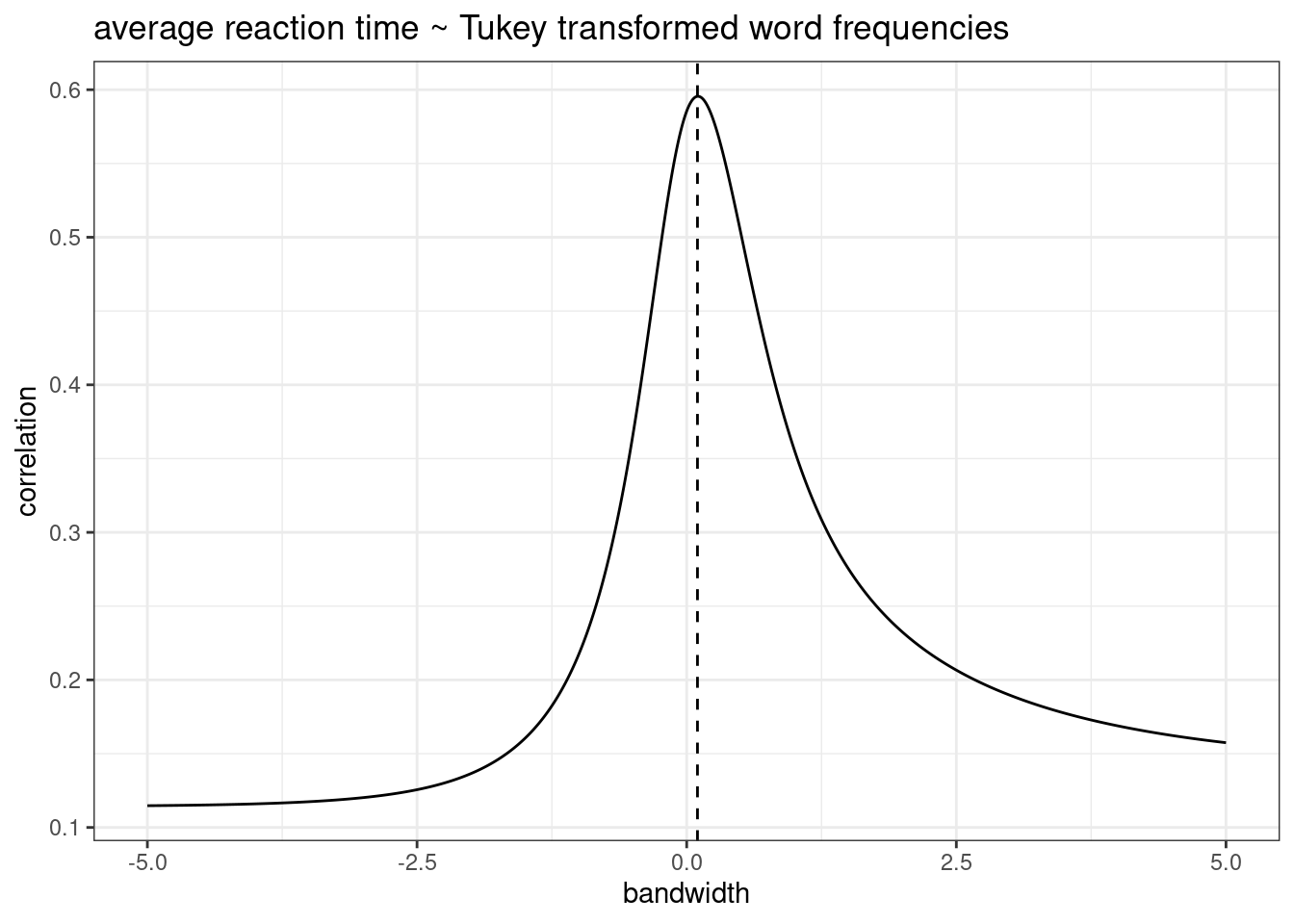

• трансформация Бокса — Кокса
• …

В датасет собрана частотность разных лемм на основании корпуса НКРЯ (Ляшевская and Шаров 2009) (в датасете только значения больше ipm > 10). Известно, что частотность слова связана с рангом слова (см. закон Ципфа). Постройте переменную ранга и визуализируйте связь ранга и логорифма частотности с разбивкой по частям речи. Какие части речи так и не приобрели после трансформации “приемлимую” линейную форму? (я насчитал 5 таких)

a
adv
advpro
anum
apro
conj
intj
num
part
pr
s
s.PROP
spro
v

9.3 Нормальность распределение остатков

Линейная регрессия предполагает нормальность распределения остатков. Когда связь не линейна, то остатки тоже будут распределены не нормально.

Можно смотреть на первый график используя функцию plot(m1) — график остатков. Интерпретаций этого графика достаточно много (см. статью про это).

Можно смотреть на qqplot:

tibble(res = m1$residuals) %>% 
  ggplot(aes(res))+
  geom_histogram(aes(y = ..density..))+
  stat_function(fun = dnorm, args = list(mean = 0, sd = sd(m1$residuals)), color = "red")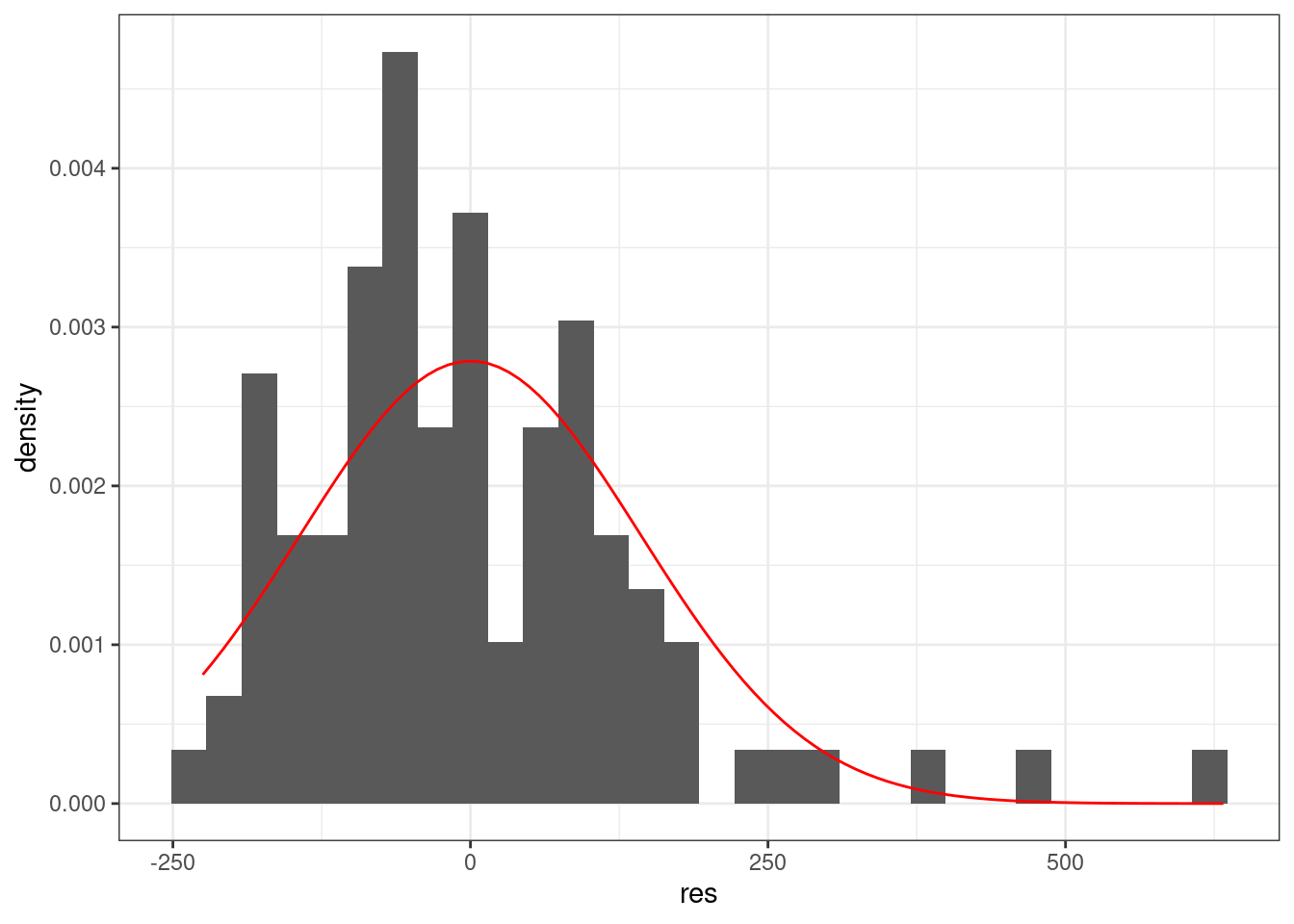

qqnorm(m1$residuals)
qqline(m1$residuals)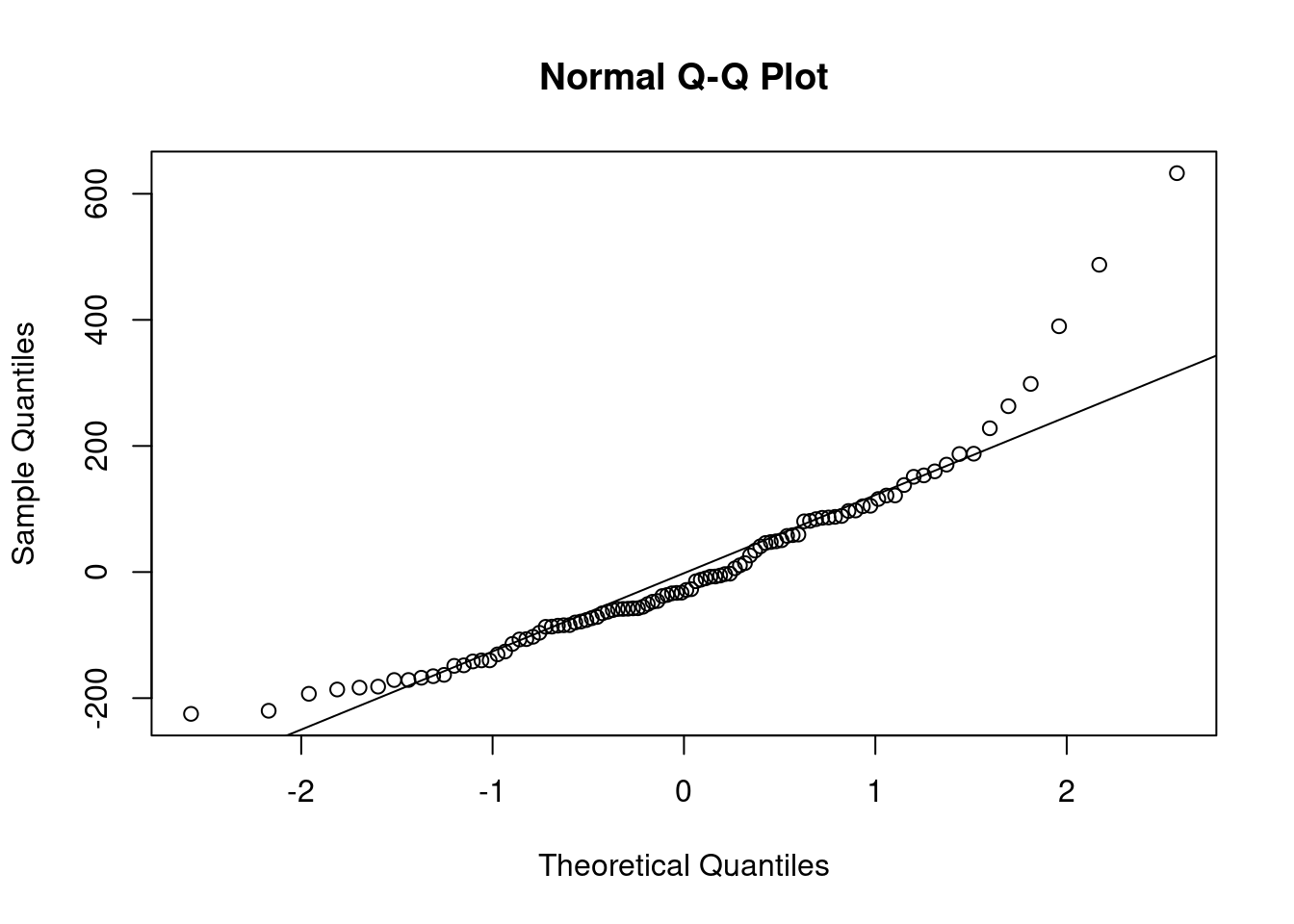

tibble(res = m2$residuals) %>% 
  ggplot(aes(res))+
  geom_histogram(aes(y = ..density..))+
  stat_function(fun = dnorm, args = list(mean = 0, sd = sd(m2$residuals)), color = "red")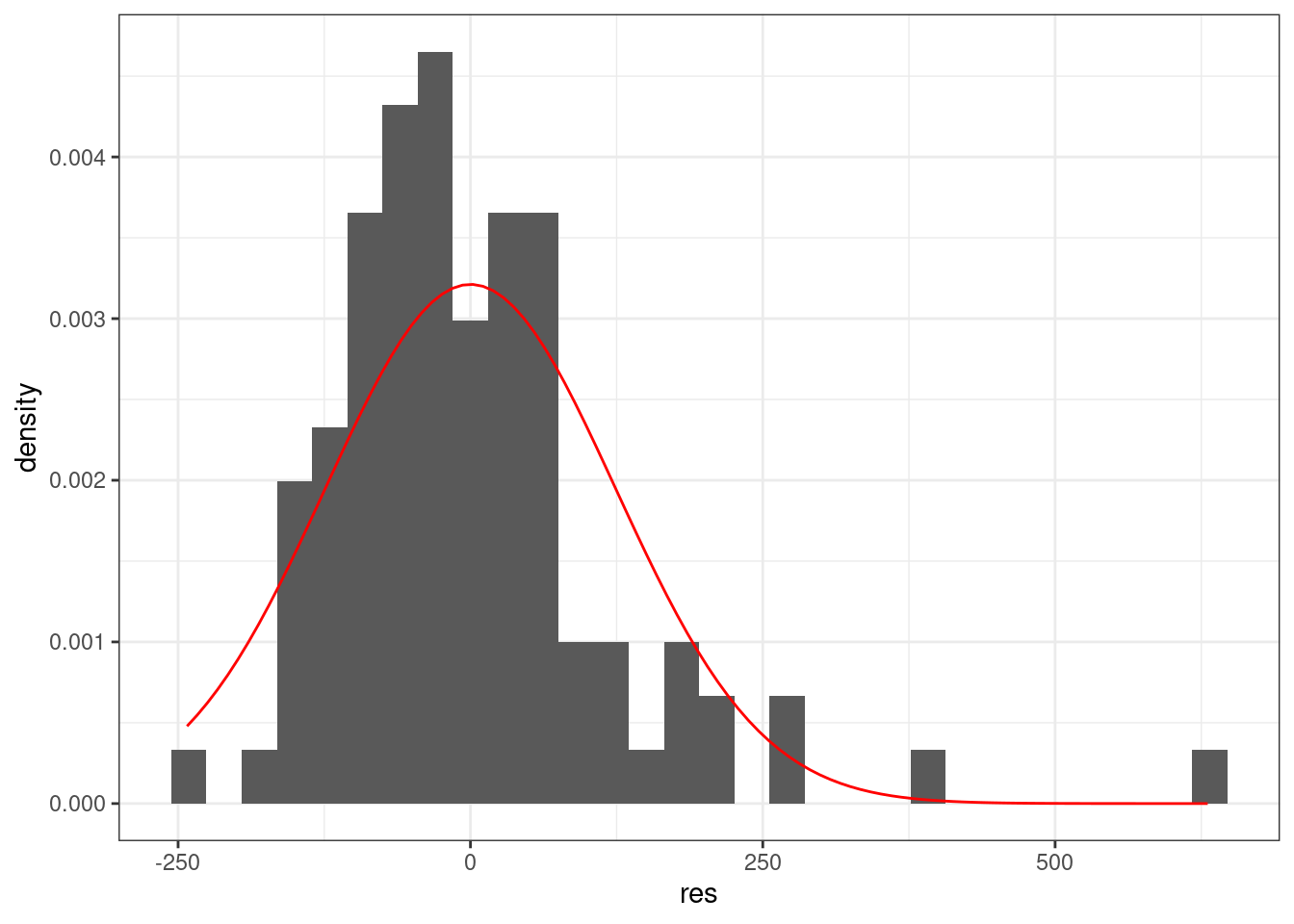

qqnorm(m2$residuals)
qqline(m2$residuals)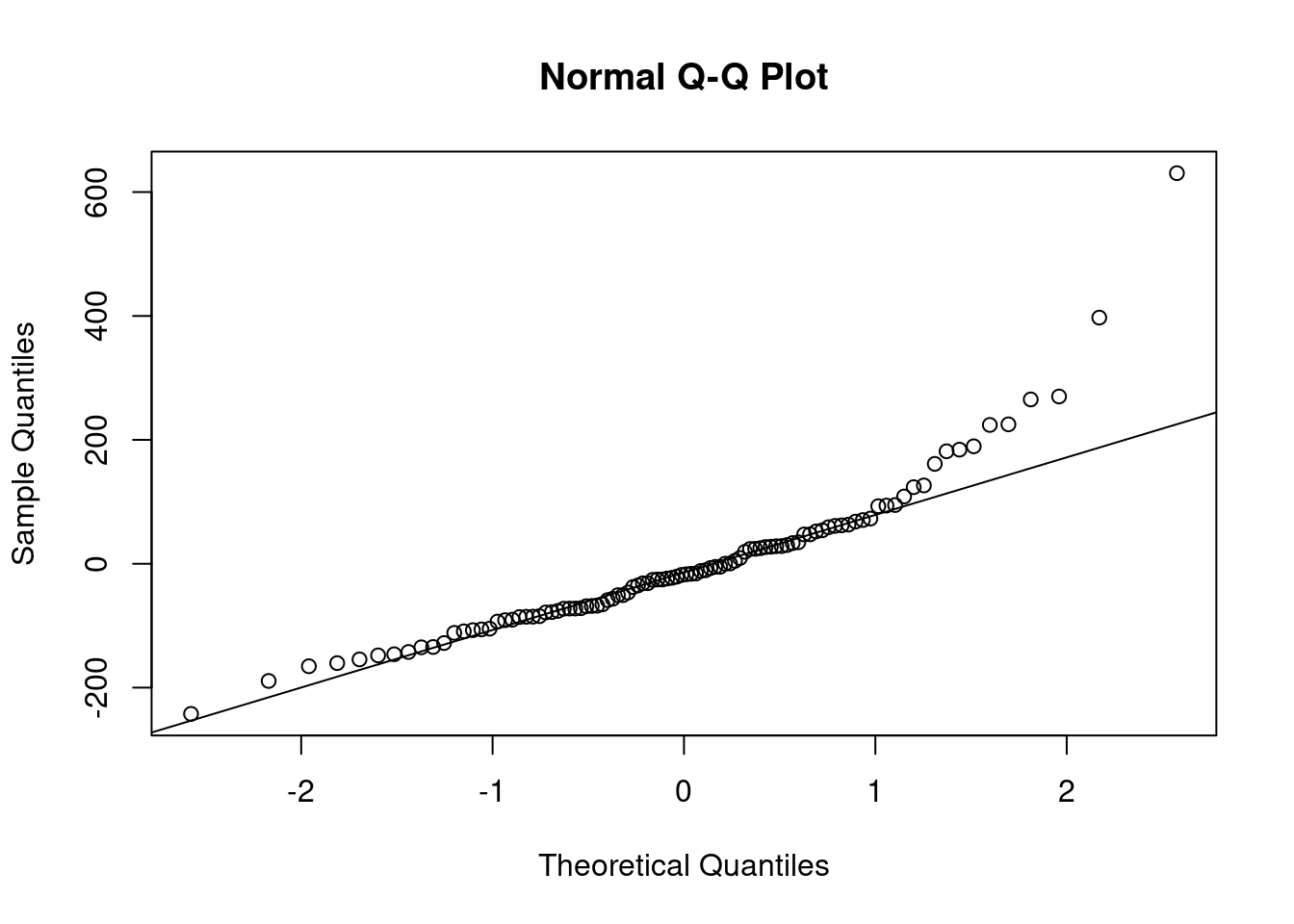

tibble(res = m3$residuals) %>% 
  ggplot(aes(res))+
  geom_histogram(aes(y = ..density..))+
  stat_function(fun = dnorm, args = list(mean = 0, sd = sd(m3$residuals)), color = "red")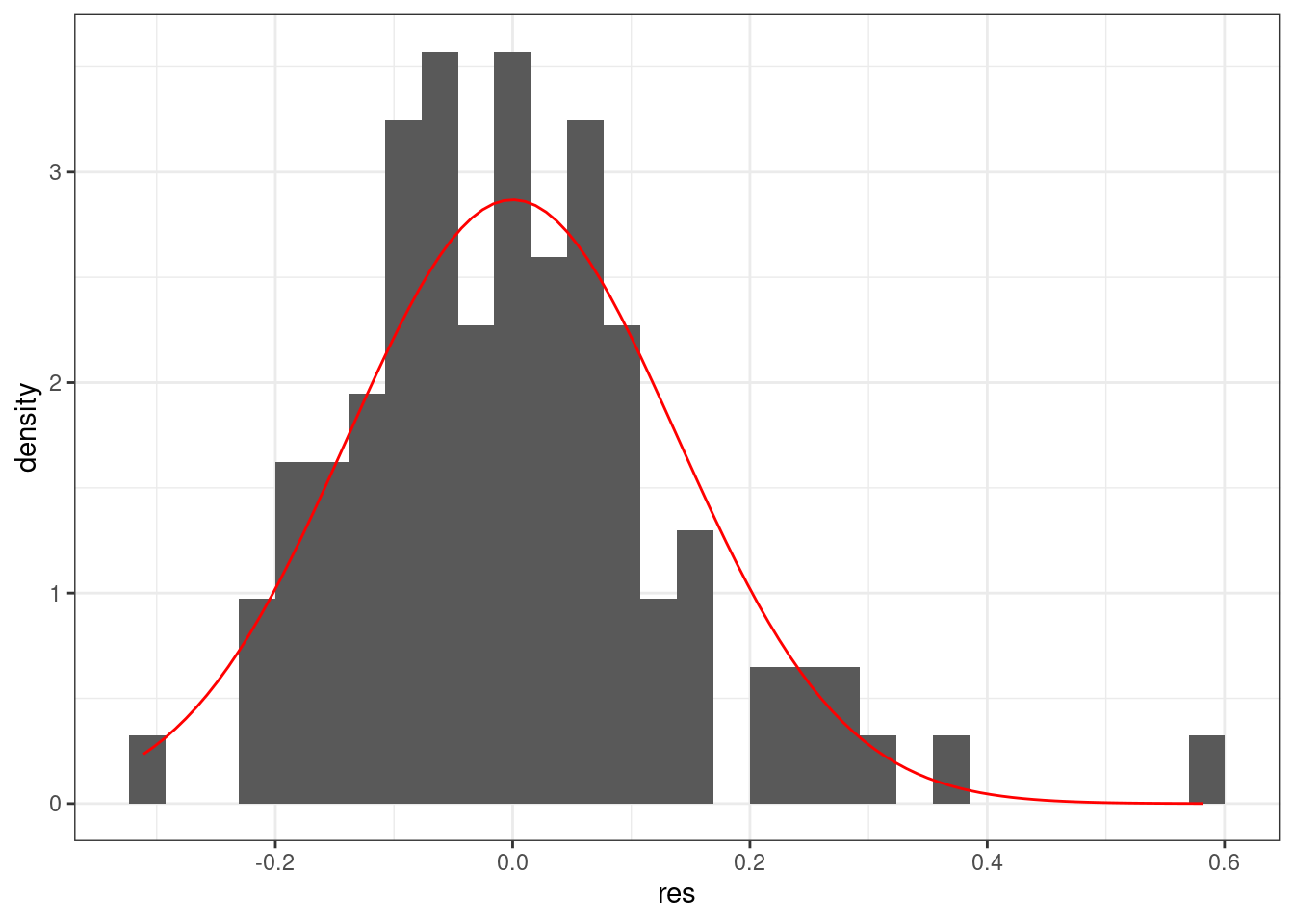

qqnorm(m3$residuals)
qqline(m3$residuals)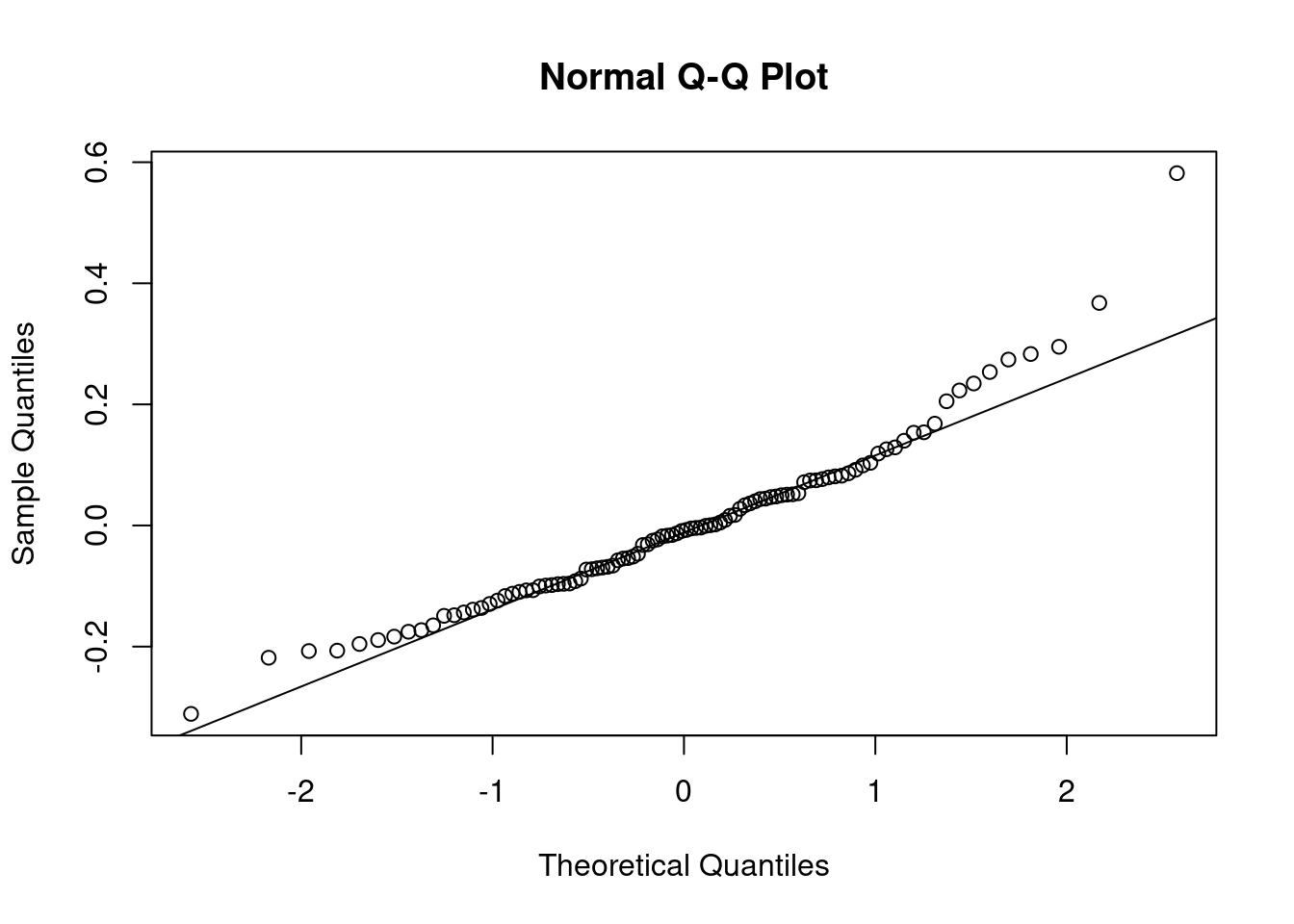

9.4 Гетероскидастичность

Распределение остатков непостоянно (т.е. не гомоскидастичны):

ldt %>% 
  ggplot(aes(Mean_RT, Freq))+
  geom_point()+
  theme_bw()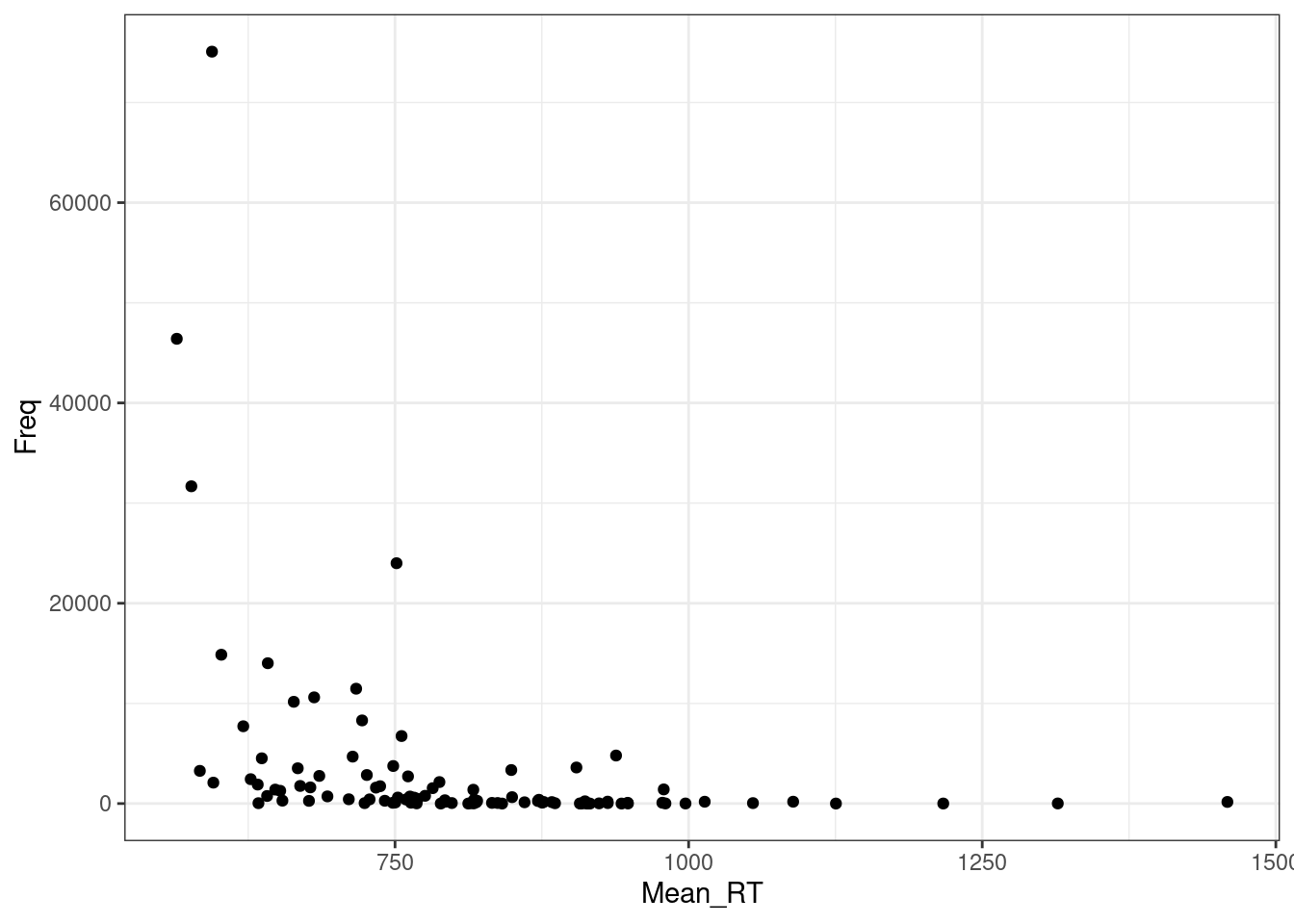

Тоже решается преобазованием данных.

9.5 Мультиколлинеарность

Линейная связь между некоторыми предикторами в модели.

• корреляционная матрица
• VIF (Variance inflation factor), car::vif()
  • VIF = 1 (Not correlated)
  • 1 < VIF < 5 (Moderately correlated)
  • VIF >=5 (Highly correlated)

9.6 Независимость наблюдений

Наблюдения должны быть независимы. В ином случае нужно использовать модель со смешанными эффектами.

9.6.1 Линейная модель со смешанными эффектами

В качестве примера мы попробуем поиграть с законом Хердана-Хипса, описывающий взаимосвязь количества уникальных слов в тексте в зависимости от длины текста. В датасете собрано шесть корпусов Universal Dependencies (Zeman et al. 2020) и некоторые числа, посчитанные на их основании:

ud <- read_csv("https://raw.githubusercontent.com/agricolamz/2021_da4l/master/data/ud_corpora.csv")

ud %>% 
  ggplot(aes(n_words, n_tokens))+
  geom_point()+
  facet_wrap(~corpus, scale = "free")+
  geom_smooth(method = "lm", se = FALSE)+
  labs(x = "количество слов", 
       y = "количество уникальных слов",
       caption = "данные корпусов Universal Dependencies")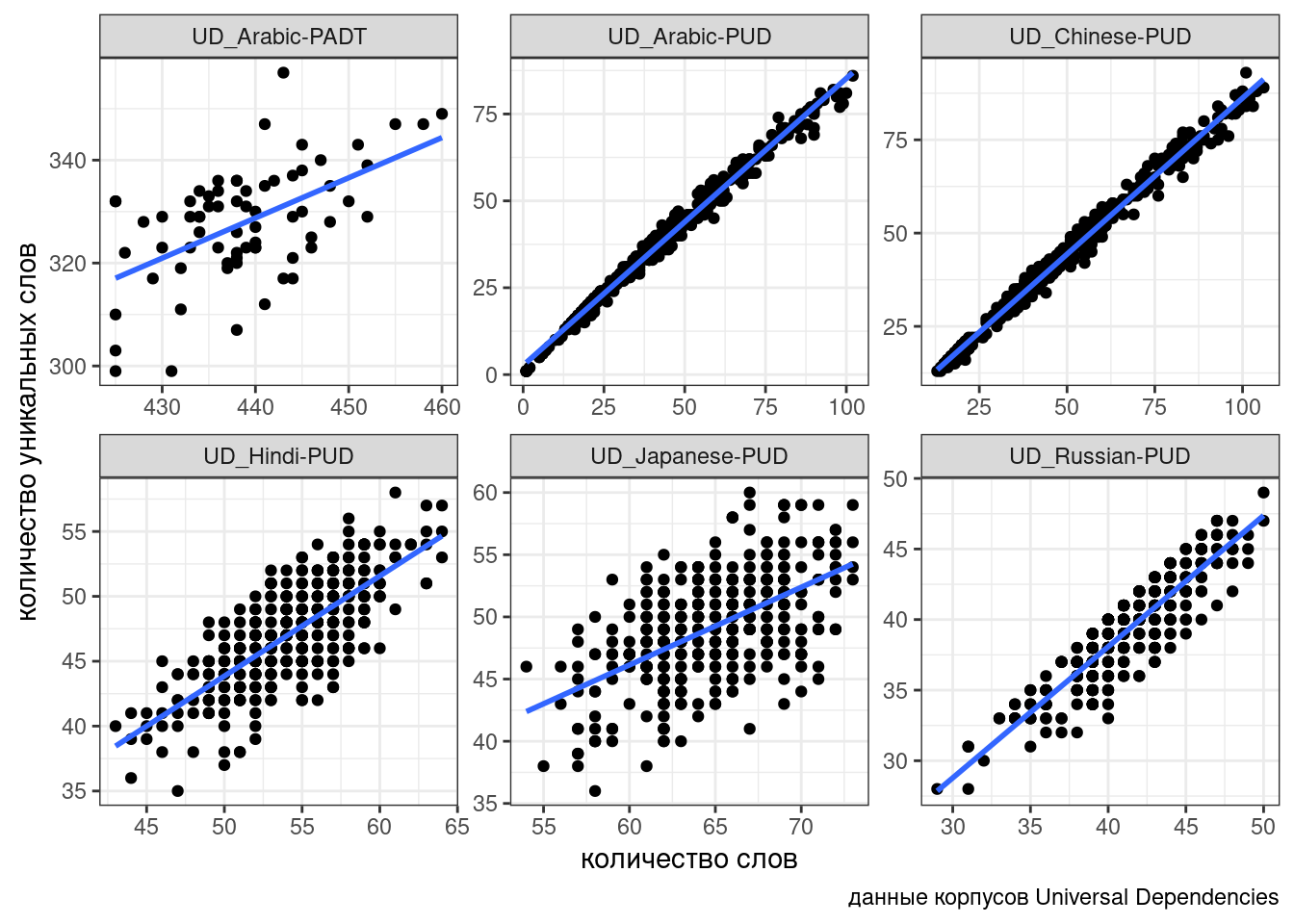

Связь между переменными безусловно линейная, однако в разных корпусах представлена разная перспектива: для каких-то корпусов, видимо, тексты специально нарезались, так что тексты таких корпусов содержат от 30-40 до 50-80 слов, а какие-то оставались не тронутыми. Чтобы показать, что связь есть, нельзя просто “слить” все наблюдения в один котел (см. парадокс Симпсона), так как это нарушит предположение регрессии о независимости наблюдений. Мы не можем включить переменную corpus в качестве dummy-переменной: тогда один из корпусов попадет в интерсепт (станет своего рода базовым уровенем), а остальные будут от него отсчитываться. К тому же не очень понятно, как работать с новыми данными из других корпусов: ведь мы хотим предсказывать значения обобщенно, вне зависимости от корпуса.

При моделировании при помощи моделей со случайными эффектами различают:

• основные эффекты – это те связи, которые нас интересуют, независимые переменные (количество слов, количество уникальных слов);
• случайные эффекты – это те переменные, которые создают группировку в данных (корпус).

В результате моделирования появляется обобщенная модель, которая игнорирует группировку, а потом для каждого значения случайного эффекта генерируется своя регрессия, отсчитывая от обобщенной модели как от базового уровня.

Рассмотрим простейший случай:

library(lme4)
library(lmerTest)

fit1 <- lmer(n_tokens~n_words+(1|corpus), data = ud)
summary(fit1)

Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: n_tokens ~ n_words + (1 | corpus)
   Data: ud

REML criterion at convergence: 10321.5

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-7.5271 -0.4947  0.0354  0.5282  8.6350 

Random effects:
 Groups   Name        Variance Std.Dev.
 corpus   (Intercept) 240.608  15.512  
 Residual               8.844   2.974  
Number of obs: 2046, groups:  corpus, 6

Fixed effects:
               Estimate  Std. Error          df t value            Pr(>|t|)    
(Intercept)   -4.527634    6.353147    4.958748  -0.713               0.508    
n_words        0.827933    0.004418 1992.686553 187.415 <0.0000000000000002 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
        (Intr)
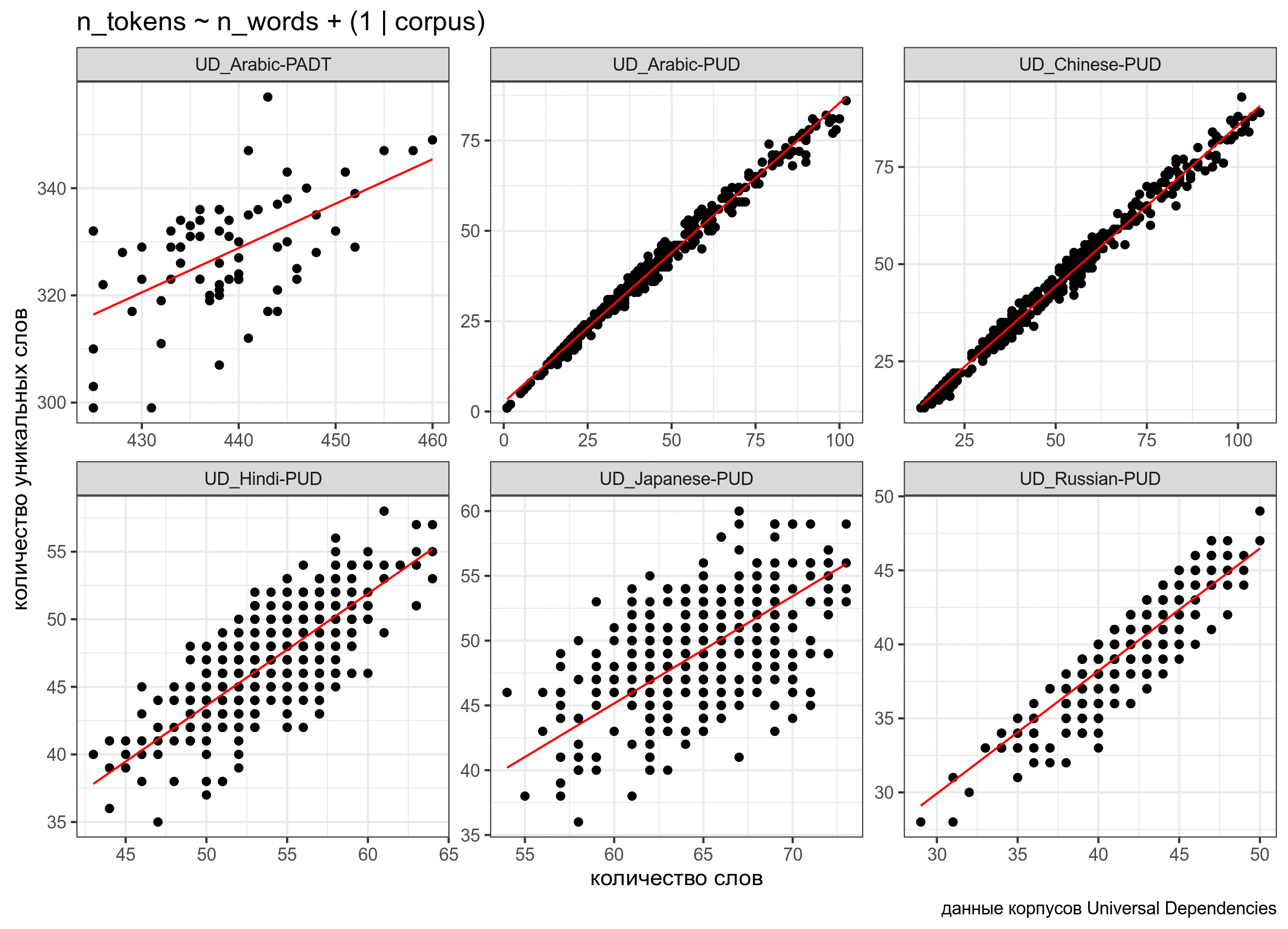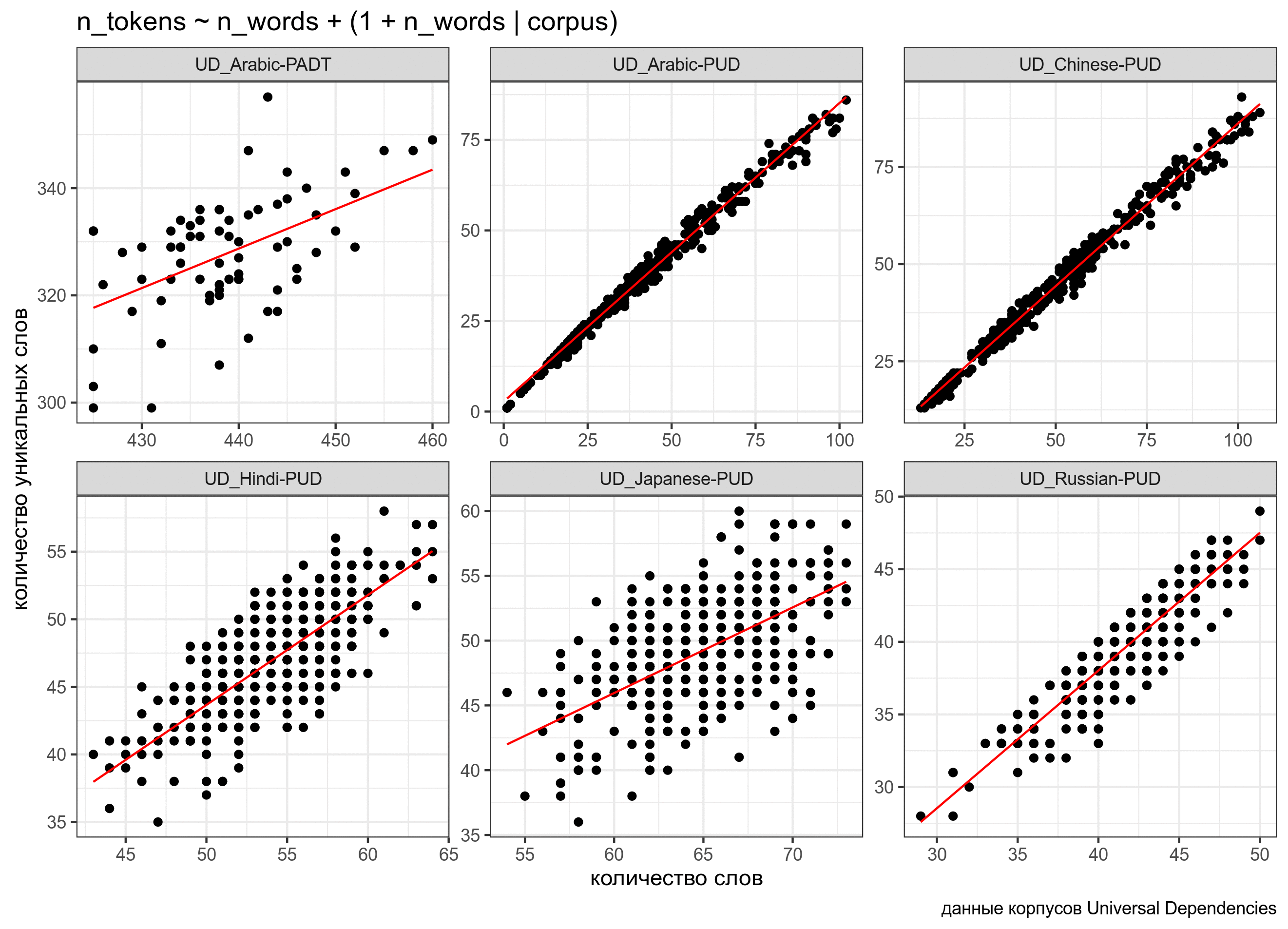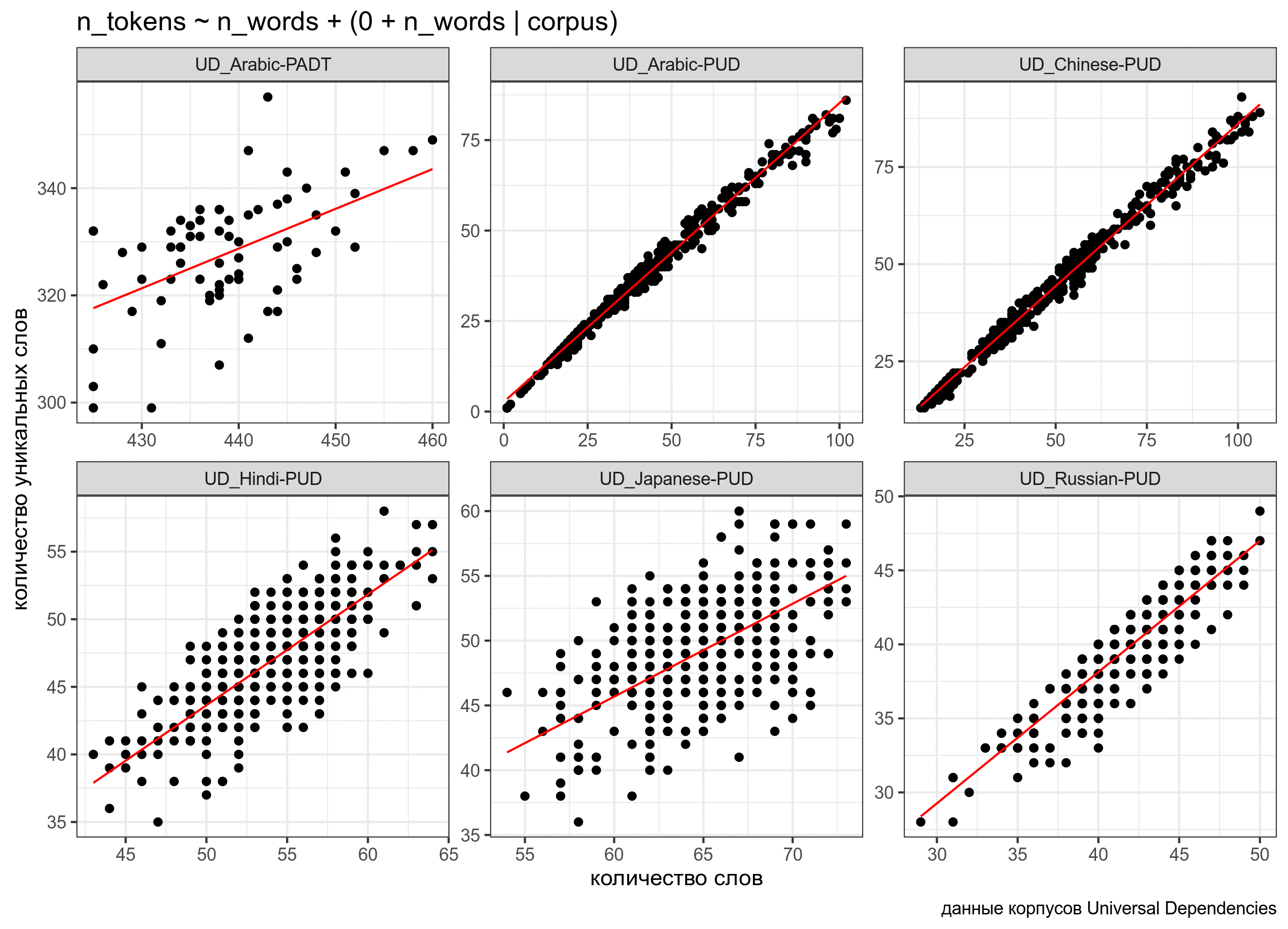
n_words -0.079

ud %>% 
  mutate(predicted = predict(fit1)) %>% 
  ggplot(aes(n_words, n_tokens))+
  geom_point()+
  facet_wrap(~corpus, scale = "free")+
  geom_line(aes(y = predicted), color = "red") +
  labs(x = "количество слов", 
       y = "количество уникальных слов",
       caption = "данные корпусов Universal Dependencies")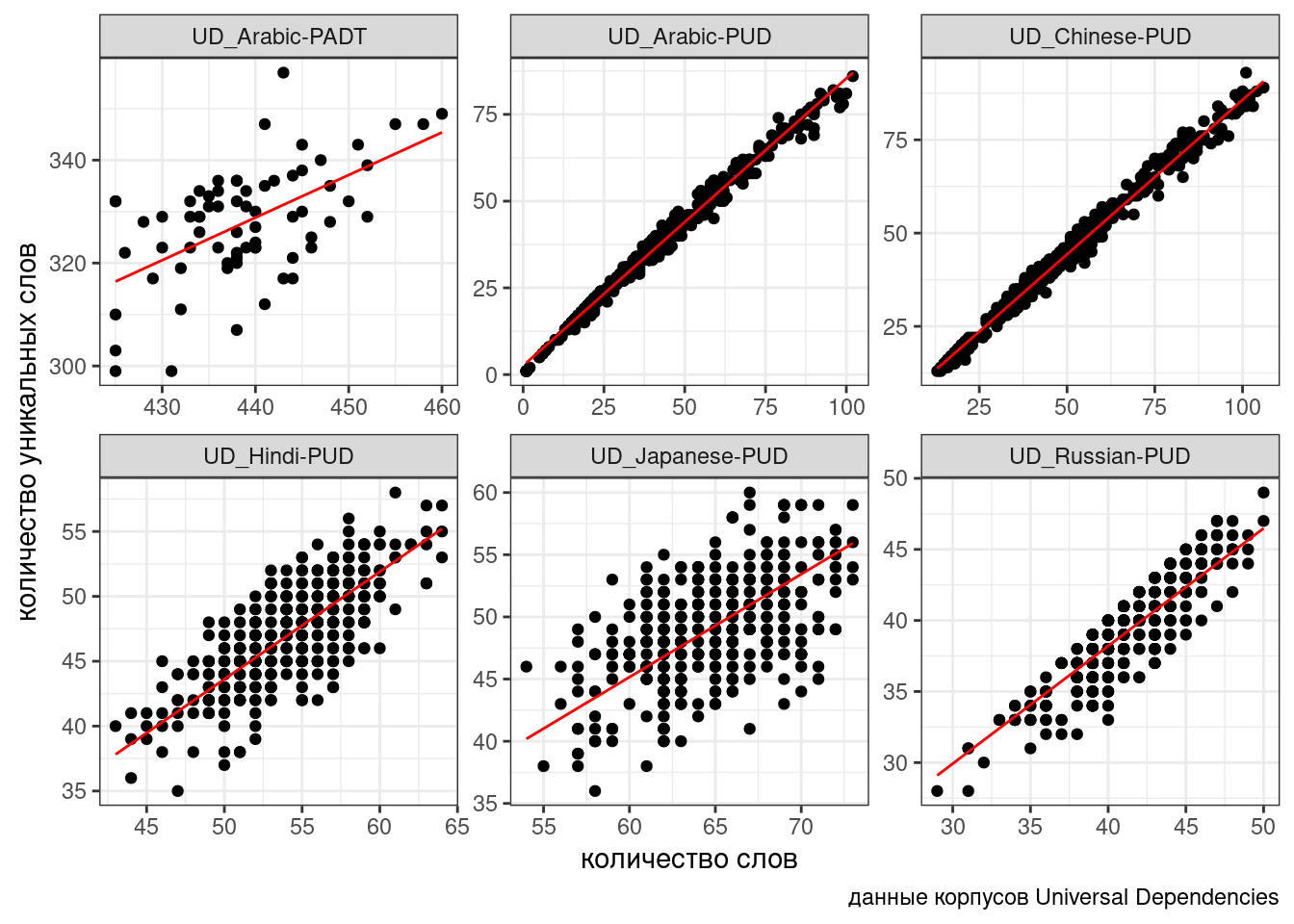

В данном случае мы предполагаем, что случайный эффект имеет случайный свободный член. Т.е. все получающиеся линии параллельны, так как имеют общий угловой коэффициент. Можно допустить большую свободу и сделать так, чтобы в случайном эффекте были не только интерсепт, но и свободный член:

fit2 <- lmer(n_tokens~n_words+(1+n_words|corpus), data = ud)
summary(fit2)

Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: n_tokens ~ n_words + (1 + n_words | corpus)
   Data: ud

REML criterion at convergence: 10275.2

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-7.8337 -0.5003  0.0293  0.5172  8.8405 

Random effects:
 Groups   Name        Variance Std.Dev. Corr 
 corpus   (Intercept) 4.465751 2.11323       
          n_words     0.009532 0.09763  -1.00
 Residual             8.693060 2.94840       
Number of obs: 2046, groups:  corpus, 6

Fixed effects:
            Estimate Std. Error      df t value  Pr(>|t|)    
(Intercept)  3.23103    0.88937 2.21775   3.633    0.0582 .  
n_words      0.80323    0.04005 4.10414  20.056 0.0000299 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
        (Intr)
n_words -0.988
optimizer (nloptwrap) convergence code: 0 (OK)
boundary (singular) fit: see ?isSingular

ud %>% 
  mutate(predicted = predict(fit2)) %>% 
  ggplot(aes(n_words, n_tokens))+
  geom_point()+
  facet_wrap(~corpus, scale = "free")+
  geom_line(aes(y = predicted), color = "red") +
  labs(x = "количество слов", 
       y = "количество уникальных слов",
       caption = "данные корпусов Universal Dependencies")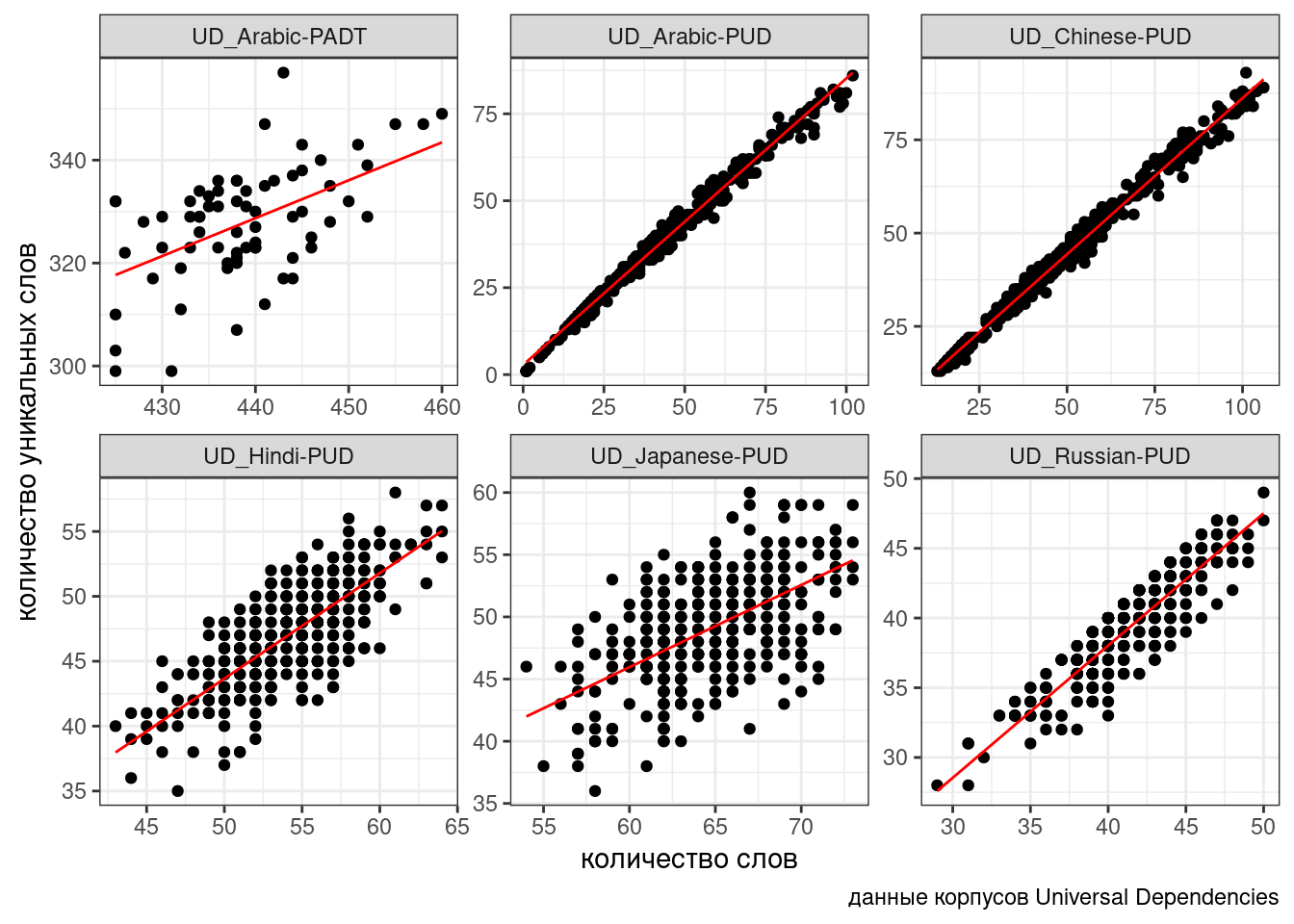

При желании мы можем также построить модель, в которой в случайном эффекте будет лишь угловой коэффициент, а свободный член будет фиксированным:

fit3 <- lmer(n_tokens~n_words+(0+n_words|corpus), data = ud)
summary(fit3)

Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: n_tokens ~ n_words + (0 + n_words | corpus)
   Data: ud

REML criterion at convergence: 10280.9

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-7.8107 -0.4933  0.0315  0.5227  8.8209 

Random effects:
 Groups   Name    Variance Std.Dev.
 corpus   n_words 0.004023 0.06343 
 Residual         8.717996 2.95263 
Number of obs: 2046, groups:  corpus, 6

Fixed effects:
              Estimate Std. Error         df t value             Pr(>|t|)    
(Intercept)    2.64805    0.21627 2043.59791   12.24 < 0.0000000000000002 ***
n_words        0.80427    0.02615    5.16230   30.76          0.000000477 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
        (Intr)
n_words -0.132

ud %>% 
  mutate(predicted = predict(fit3)) %>% 
  ggplot(aes(n_words, n_tokens))+
  geom_point()+
  facet_wrap(~corpus, scale = "free")+
  geom_line(aes(y = predicted), color = "red") +
  labs(x = "количество слов", 
       y = "количество уникальных слов",
       caption = "данные корпусов Universal Dependencies")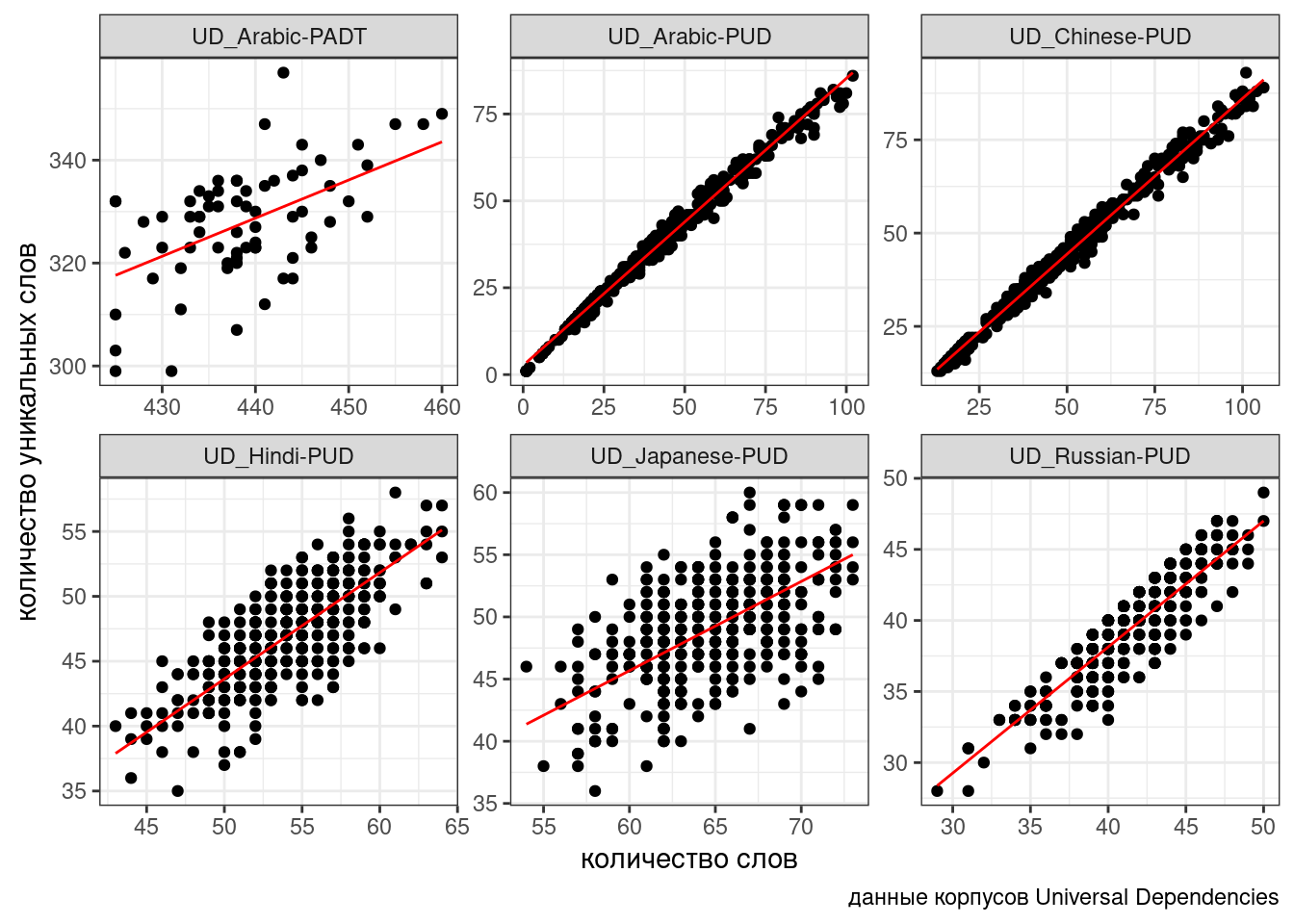

Линии получились очень похожими, но разными:

Сравним полученные модели:

anova(fit3, fit2, fit1)

Визуализируйте полученные модели при помощи функции plot(). Какие ограничения на применение линейной регрессии нарушается в наших моделях?

Постройте модель со случайными угловым коэффициентом и свободным членом, устранив проблему, которую вы заметили в прошлом задании.

Пользуясь знаниями из предыдущих заданий, смоделируйте связь количества слов и количества существительных. С какими проблемами вы столкнулись?