10 Ограничения на применение регрессии

library(tidyverse)

10.1 Дисперсия и стандартное отклонение

Дисперсия — мера разброса значений наблюдений относительно среднего.

\[\sigma^2_X = \frac{\sum_{i = 1}^n(x_i - \bar{x})^2}{n - 1},\]

где

• \(x_1, ..., x_n\) — наблюдения;
• \(\bar{x}\) — среднее всех наблюдений;
• \(X\) — вектор всех наблюдений;
• \(n\) — количество наблюдений.

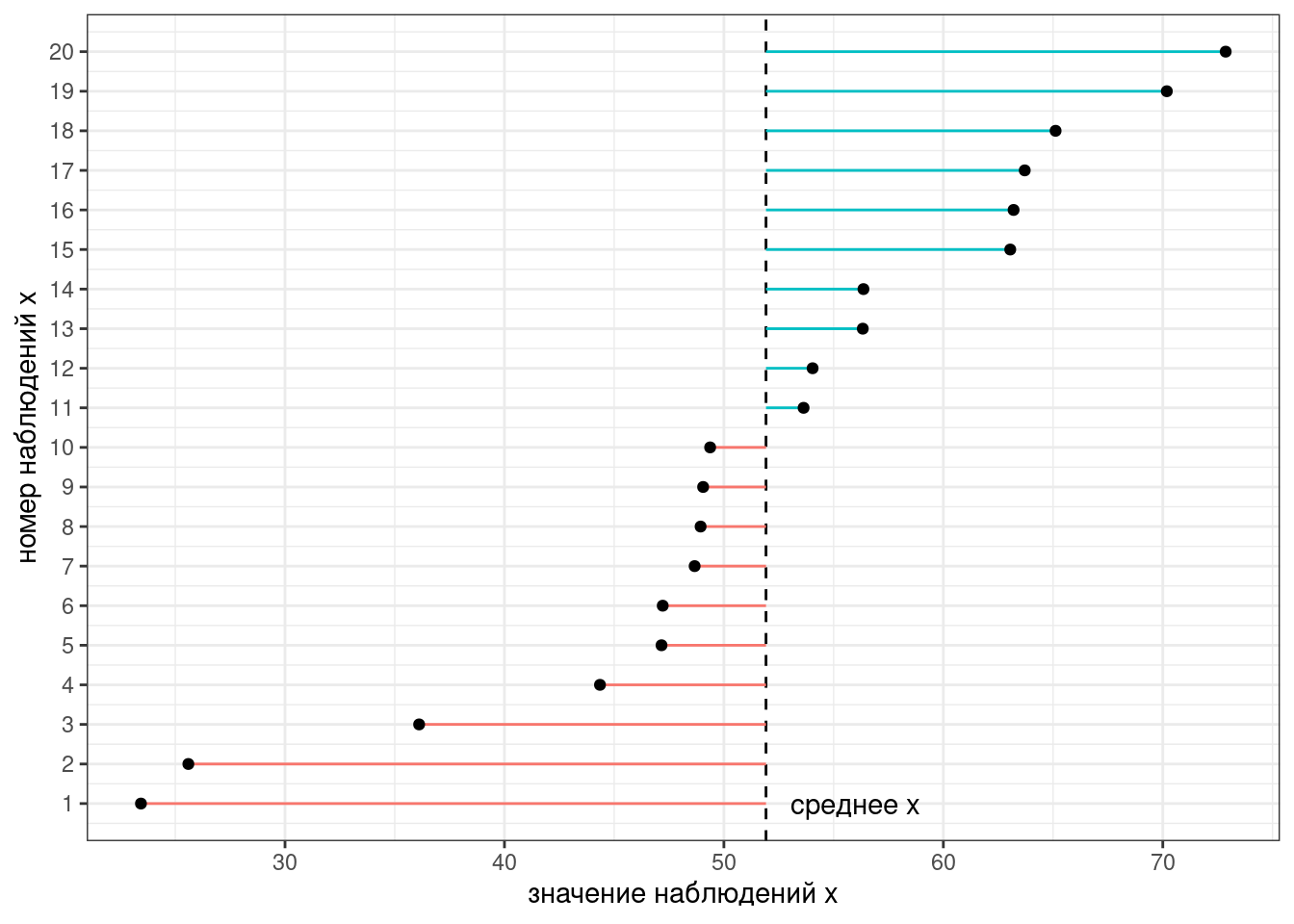
Представим, что у нас есть следующие данные:

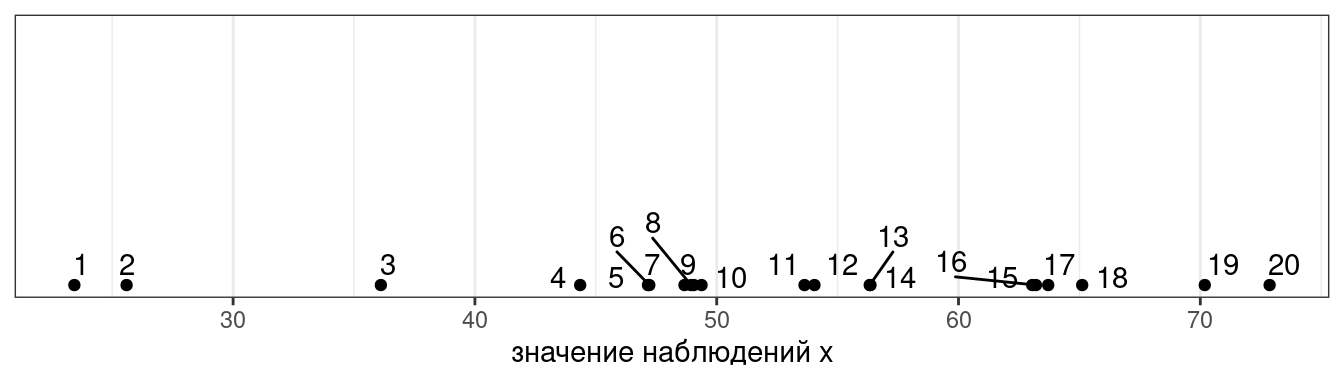
Тогда дисперсия — это сумма квадратов расстояний от каждой точки до среднего выборки (пунктирная линия) разделенное на количество наблюдений - 1 (по духу эта мера — обычное среднее, но если вас инетересует разница смещенной и несмещенной оценки дисперсии, см. видео).

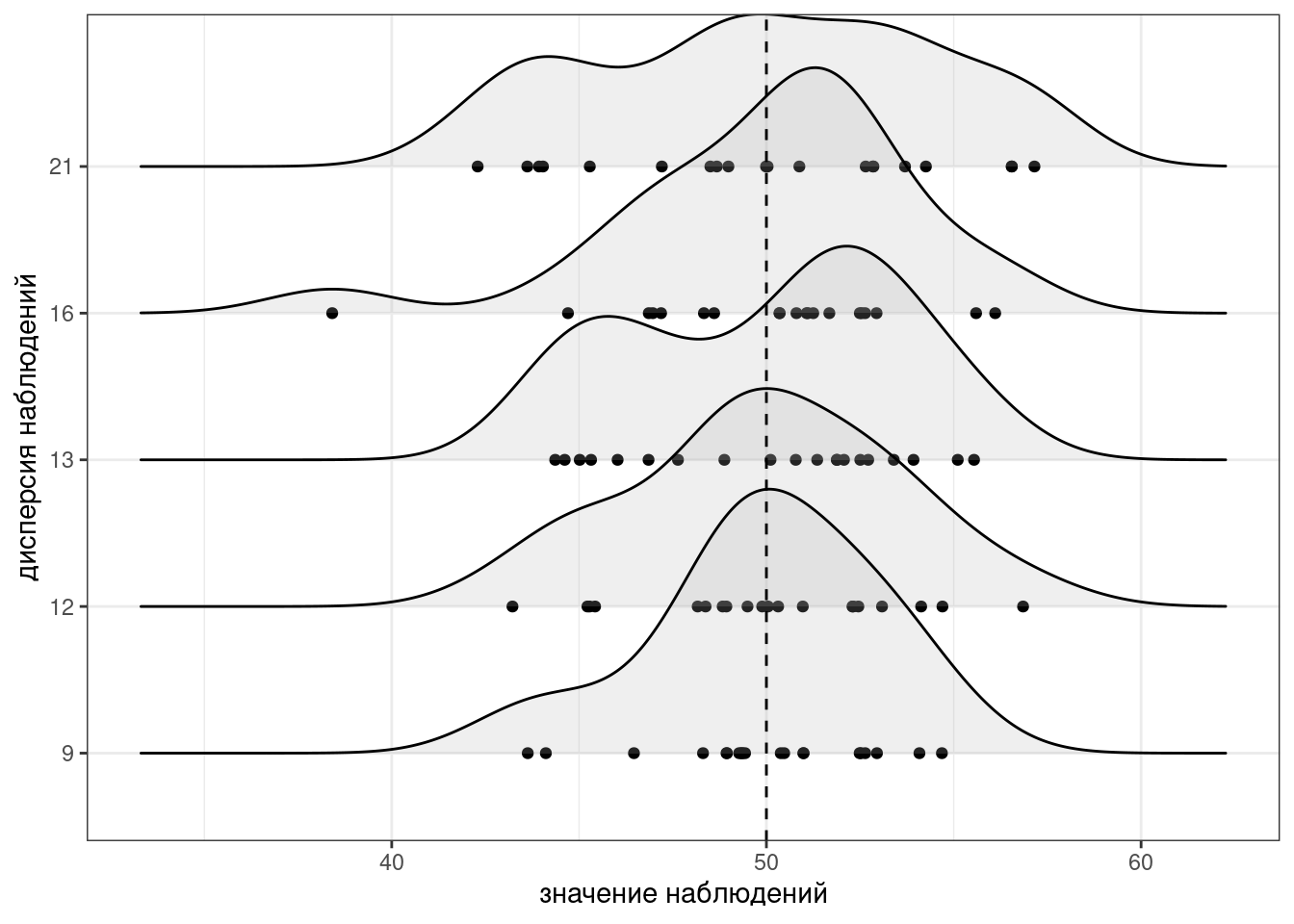
Для того чтобы было понятнее, что такое дисперсия, давайте рассмотрим несколько расспределений с одним и тем же средним, но разными дисперсиями:

В R дисперсию можно посчитать при помощи функции var()².

set.seed(42)
x <- rnorm(20, mean = 50, sd = 10)
var(x)

[1] 172.2993

Проверим, что функция выдает то же, что мы записали в формуле.

var(x) == sum((x - mean(x))^2)/(length(x)-1)

[1] TRUE

Так как дисперсия является квадратом отклонения, то часто вместо нее используют более интерпретируемое стандартное отклонение \(\sigma\) — корень из дисперсии. В R ее можно посчитать при помощи функции sd():

sd(x)

[1] 13.12628

sd(x) == sqrt(var(x))

[1] TRUE

10.2 Ковариация

Ковариация — эта мера ассоциации двух переменных.

\[cov(X, Y) = \frac{\sum_{i = 1}^n(x_i - \bar{x})(y_i-\bar{y})}{n - 1},\]

где

• \((x_1, y_1), ..., (x_n, y_n)\) — пары наблюдений;
• \(\bar{x}, \bar{y}\) — средние наблюдений;
• \(X, Y\) — векторы всех наблюдений;
• \(n\) — количество наблюдений.

Представим, что у нас есть следующие данные:

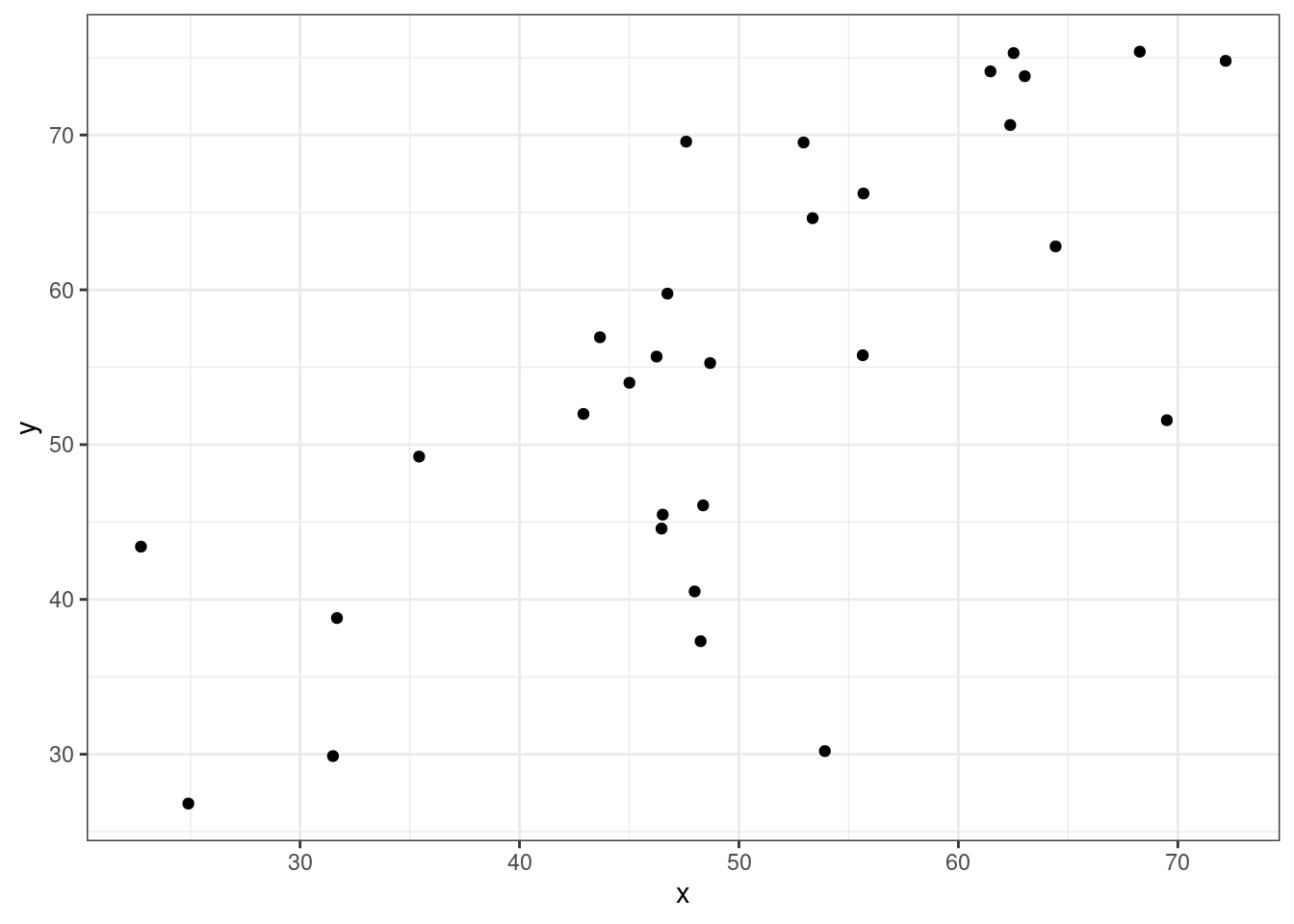
Тогда, согласно формуле, для каждой точки вычисляется следующая площадь (пуктирными линиями обозначены средние):

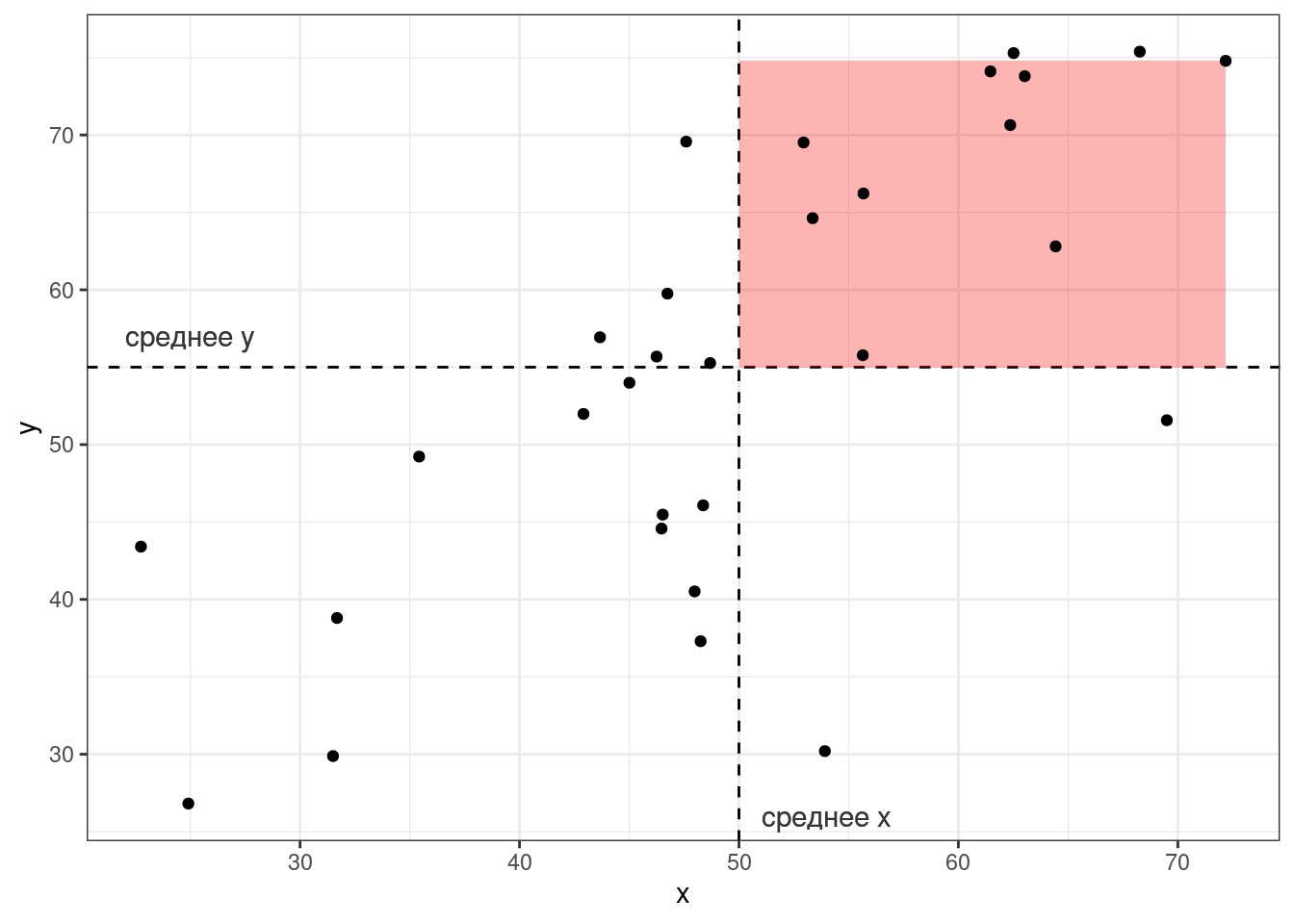
Если значения \(x_i\) и \(y_i\) какой-то точки либо оба больше, либо оба меньше средних \(\bar{x}\) и \(\bar{y}\), то получившееся произведение будет иметь знак +, если же наоборот — знак -. На графике это показано цветом.

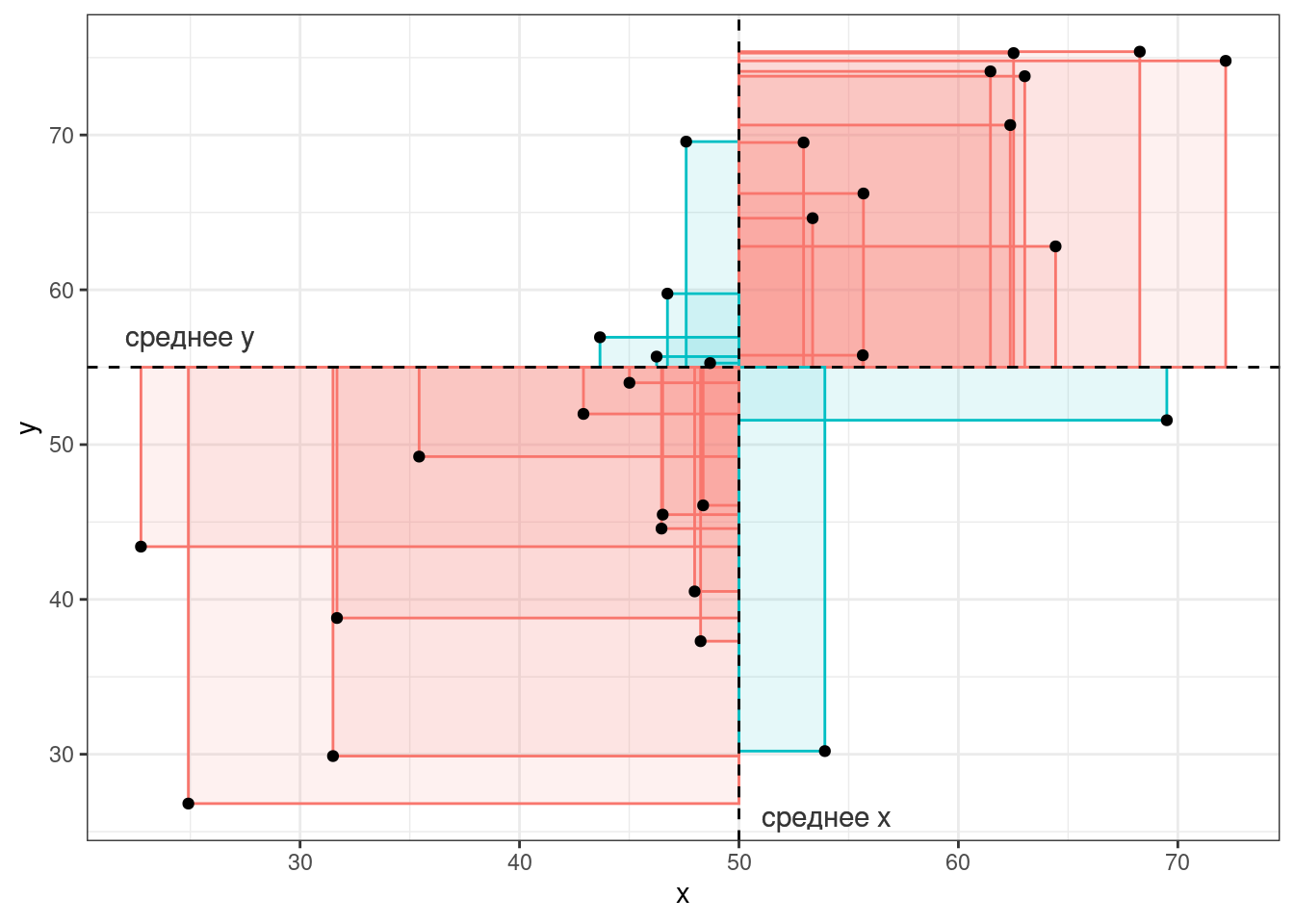
Таким образом, если много красных прямоугольников, то значение суммы будет положительное и обозначать положительную связь (чем больше \(x\), тем больше \(y\)), а если будет много синий прямоугольников, то значение суммы отрицательное и обозначать положительную связь (чем больше \(x\), тем меньше \(y\)). Непосредственно значение ковариации не очень информативно, так как может достаточно сильно варьироваться от датасета к датасету.

В R ковариацию можно посчитать при помощи функции cov().

set.seed(42)
x <- rnorm(10, mean = 50, sd = 10)
y <-  x + rnorm(10, sd = 10)
cov(x, y)

[1] 18.72204

cov(x, -y*2)

[1] -37.44407

Как видно, простое умножение на два удвоило значение ковариации, что показывает, что непосредственно ковариацию использовать для сравнения разных датасетов не стоит.

Проверим, что функция выдает то же, что мы записали в формуле.

cov(x, y) == sum((x-mean(x))*(y - mean(y)))/(length(x)-1)

[1] TRUE

10.3 Корреляция

Корреляция — это мера ассоциации/связи двух числовых переменных. Помните, что бытовое применение этого термина к категориальным переменным (например, корреляция цвета глаз и успеваемость на занятиях по R) не имеет смысла с точки зрения статистики.

10.3.1 Корреляция Пирсона

Коэффициент корреляции Пирсона — базовый коэффициент ассоциации переменных, однако стоит помнить, что он дает неправильную оценку, если связь между переменными нелинейна.

\[\rho_{X,Y} = \frac{cov(X, Y)}{\sigma_X\times\sigma_Y} = \frac{1}{n-1}\times\sum_{i = 1}^n\left(\frac{x_i-\bar{x}}{\sigma_X}\times\frac{y_i-\bar{y}}{\sigma_Y}\right),\]

где

• \((x_1, y_1), ..., (x_n, y_n)\) — пары наблюдений;
• \(\bar{x}, \bar{y}\) — средние наблюдений;
• \(X, Y\) — векторы всех наблюдений;
• \(n\) — количество наблюдений.

Последнее уравнение показывает, что коэффициент корреляции Пирсона можно представить как среднее (с поправкой, поэтому \(n-1\), а не \(n\)) произведение \(z\)-нормализованных значений двух переменных.

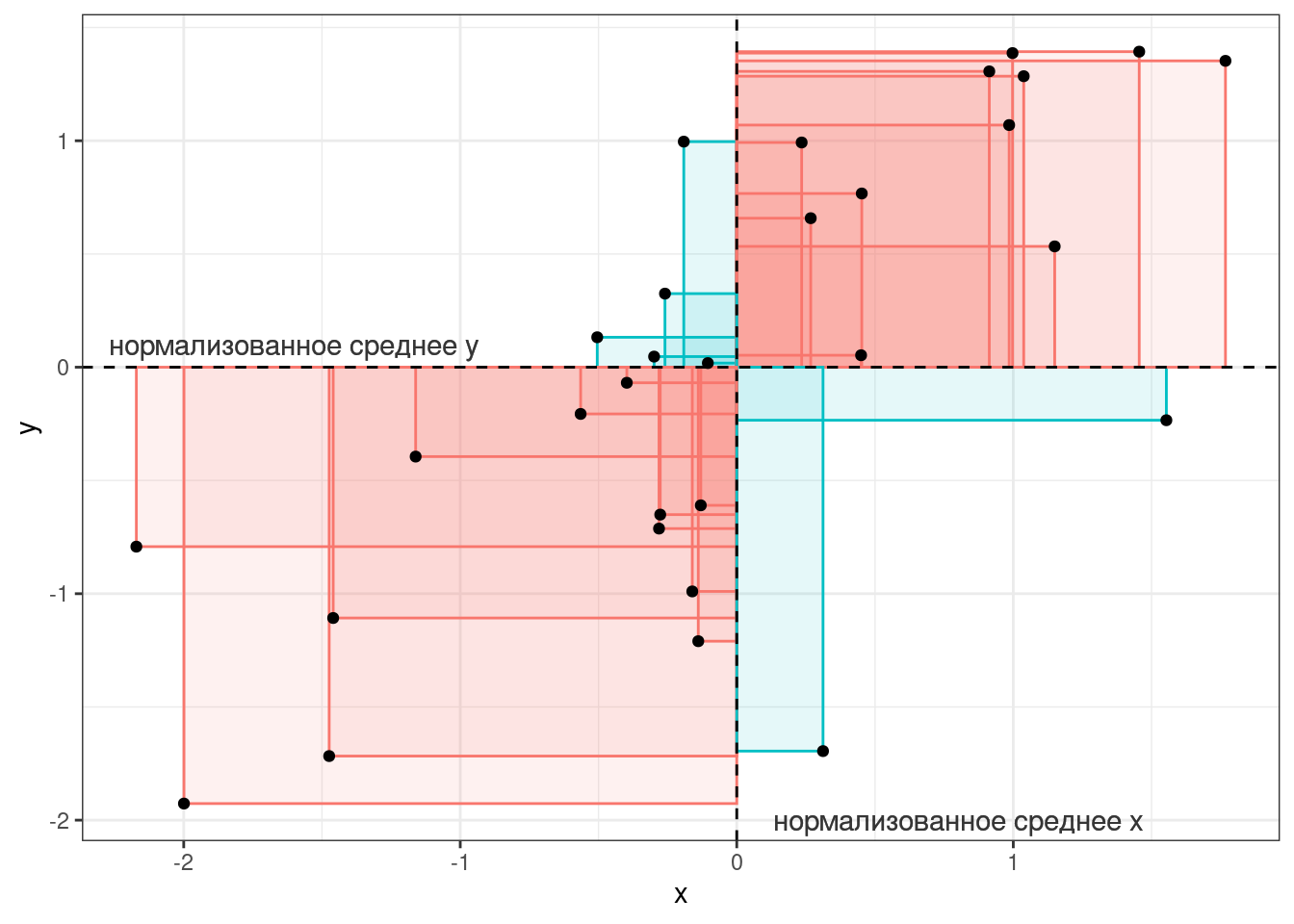
Эта нормализация приводит к тому, что

• значения корреляции имеют те же свойства знака коэффициента что и ковариация:
  • если коэффициент положительный (т. е. много красных прямоугольников) — связь между переменными положительная (чем больше \(x\), тем больше \(y\)),
  • если коэффициент отрицательный (т. е. много синих прямоугольников) — связь между переменными отрицательная (чем больше \(x\), тем меньше \(y\));
• значение корреляции имееет независимое от типа данных интеретация:
  • если модуль коэффициента близок к 1 или ему равен — связь между переменными сильная,
  • если модуль коэффициента близок к 0 или ему равен — связь между переменными слабая.

Для того чтобы было понятнее, что такое корреляция, давайте рассмотрим несколько расспределений с разными значениями корреляции:

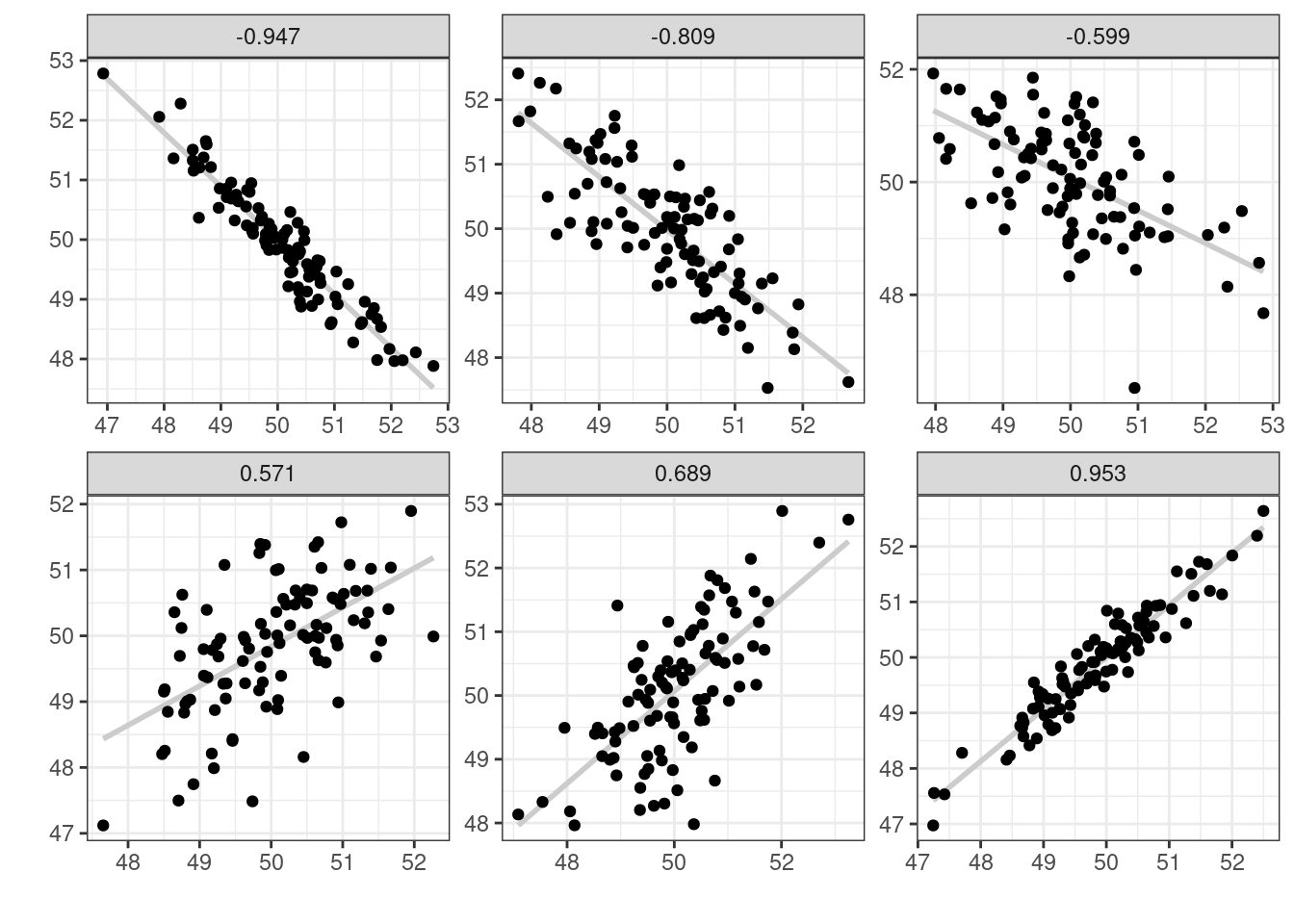
Как видно из этого графика, чем ближе модуль корреляции к 1, тем боллее компактно расположены точки друг к другу, чем ближе к 0, тем более рассеяны значения. Достаточно легко научиться приблизительно оценивать коэфициент корреляции на глаз, поиграв 2–5 минут в игру “Угадай корреляцию” здесь или здесь.

В R коэффициент корреляции Пирсона можно посчитать при помощи функции cor().

set.seed(42)
x <- rnorm(15, mean = 50, sd = 10)
y <-  x + rnorm(15, sd = 10)
cor(x, y)

[1] 0.6659041

Проверим, что функция выдает то же, что мы записали в формуле.

cor(x, y) == cov(x, y)/(sd(x)*sd(y))

[1] TRUE

cor(x, y) == sum(scale(x)*scale(y))/(length(x)-1)

[1] TRUE

10.4 Основы регрессионного анализа

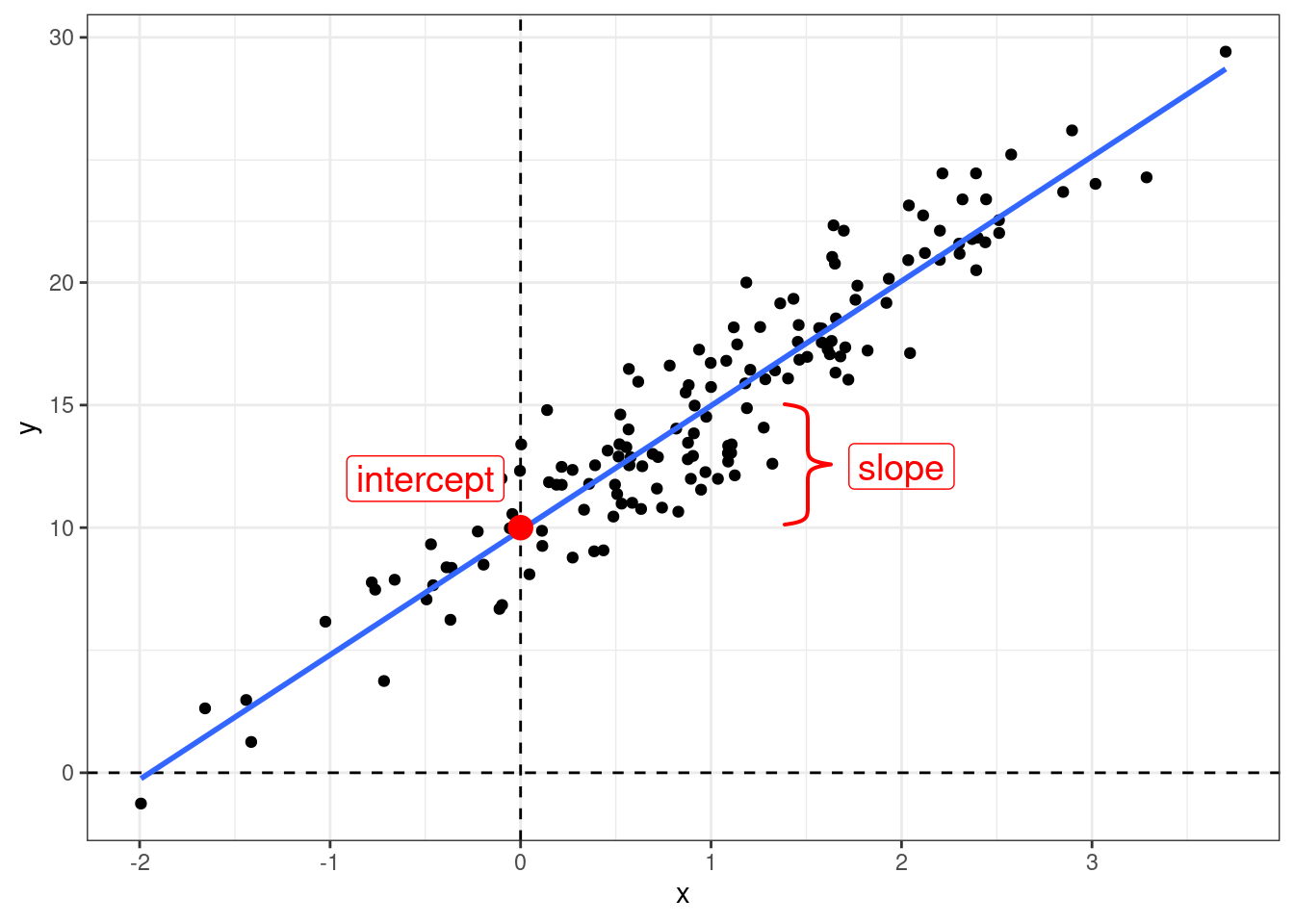
Когда мы пытаемся научиться предсказывать данные одной переменной \(Y\) при помощи другой переменной \(X\), мы получаем формулу:

\[y_i = \hat\beta_0 + \hat\beta_1 \times x_i + \epsilon_i,\] где

• \(x_i\) — \(i\)-ый элемент вектора значений \(X\);
• \(y_i\) — \(i\)-ый элемент вектора значений \(Y\);
• \(\hat\beta_0\) — оценка случайного члена (intercept);
• \(\hat\beta_1\) — оценка углового коэффициента (slope);
• \(\epsilon_i\) — \(i\)-ый остаток, разница между оценкой модели (\(\hat\beta_0 + \hat\beta_1 \times x_i\)) и реальным значением \(y_i\); весь вектор остатков иногда называют случайным шумом (на графике выделены красным).

Причем, иногда мы можем один или другой параметр считать равным нулю.

Определите по графику формулу синей прямой.

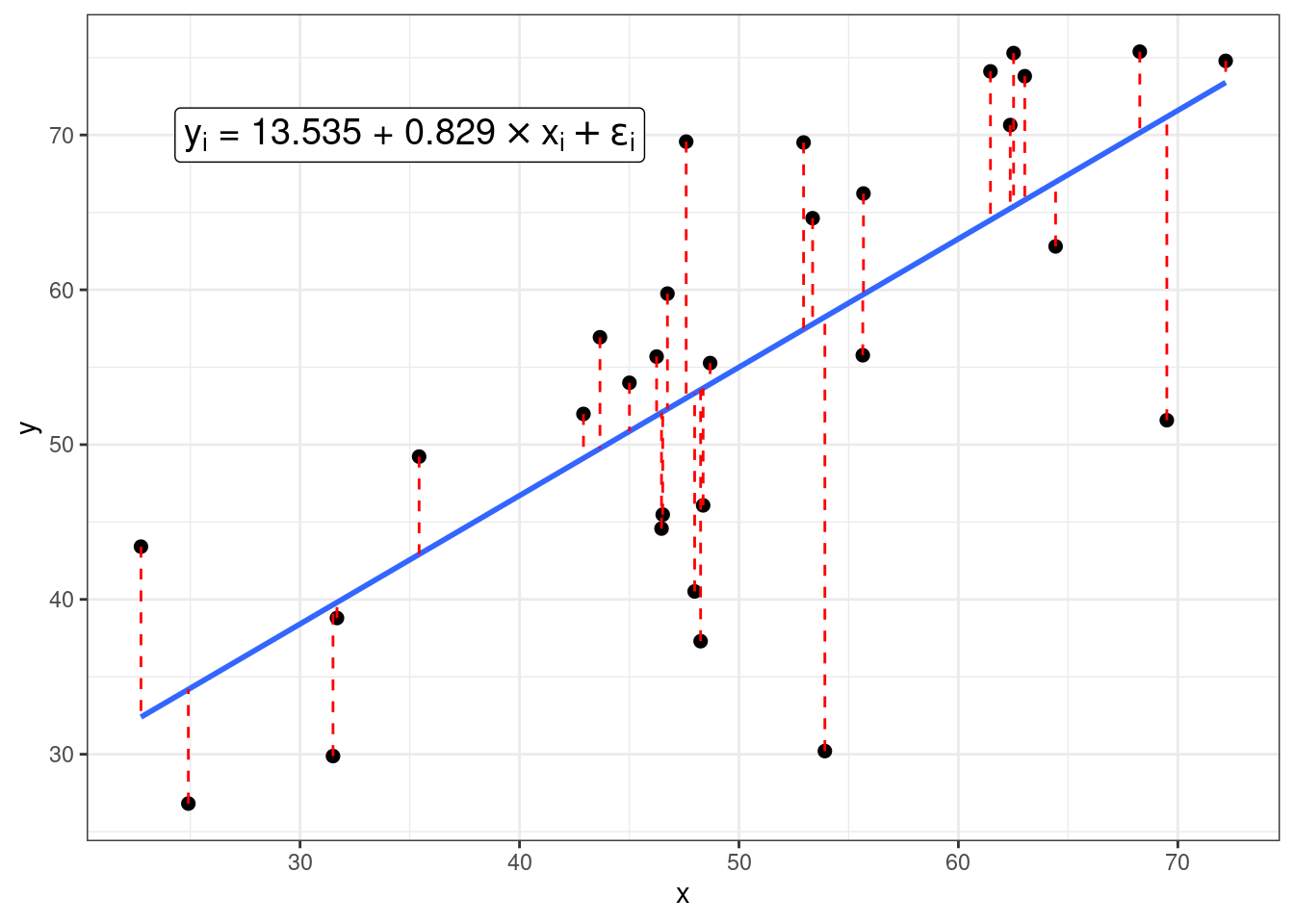
Задача регрессии — оценить параметры \(\hat\beta_0\) и \(\hat\beta_1\), если нам известны все значения \(x_i\) и \(y_i\) и мы пытаемся минимизировать значния \(\epsilon_i\). В данном конкретном случае, задачу можно решить аналитически и получить следующие формулы:

\[\hat\beta_1 = \frac{(\sum_{i=1}^n x_i\times y_i)-n\times\bar x \times \bar y}{\sum_{i = 1}^n(x_i-\bar x)^2}\]

\[\hat\beta_0 = \bar y - \hat\beta_1\times\bar x\]

При этом, вне зависимости от статистической школы, у регрессии есть свои ограничения на применение:

• линейность связи между \(x\) и \(y\);
• нормальность распределение остатков \(\epsilon_i\);
• гомоскидастичность — равномерность распределения остатков на всем протяжении \(x\);
• независимость переменных;
• независимость наблюдений друг от друга.

10.4.1 Первая регрессия

Давайте попробуем смоделировать количество слов и в рассказах М. Зощенко в зависимости от длины рассказа:

zo <- read_tsv("https://github.com/agricolamz/DS_for_DH/raw/master/data/tidy_zoshenko.csv")

zo %>% 
  filter(word == "и") %>% 
  distinct() %>% 
  ggplot(aes(n_words, n))+
  geom_point()+
  labs(x = "количество слов в рассказе",
       y = "количество и")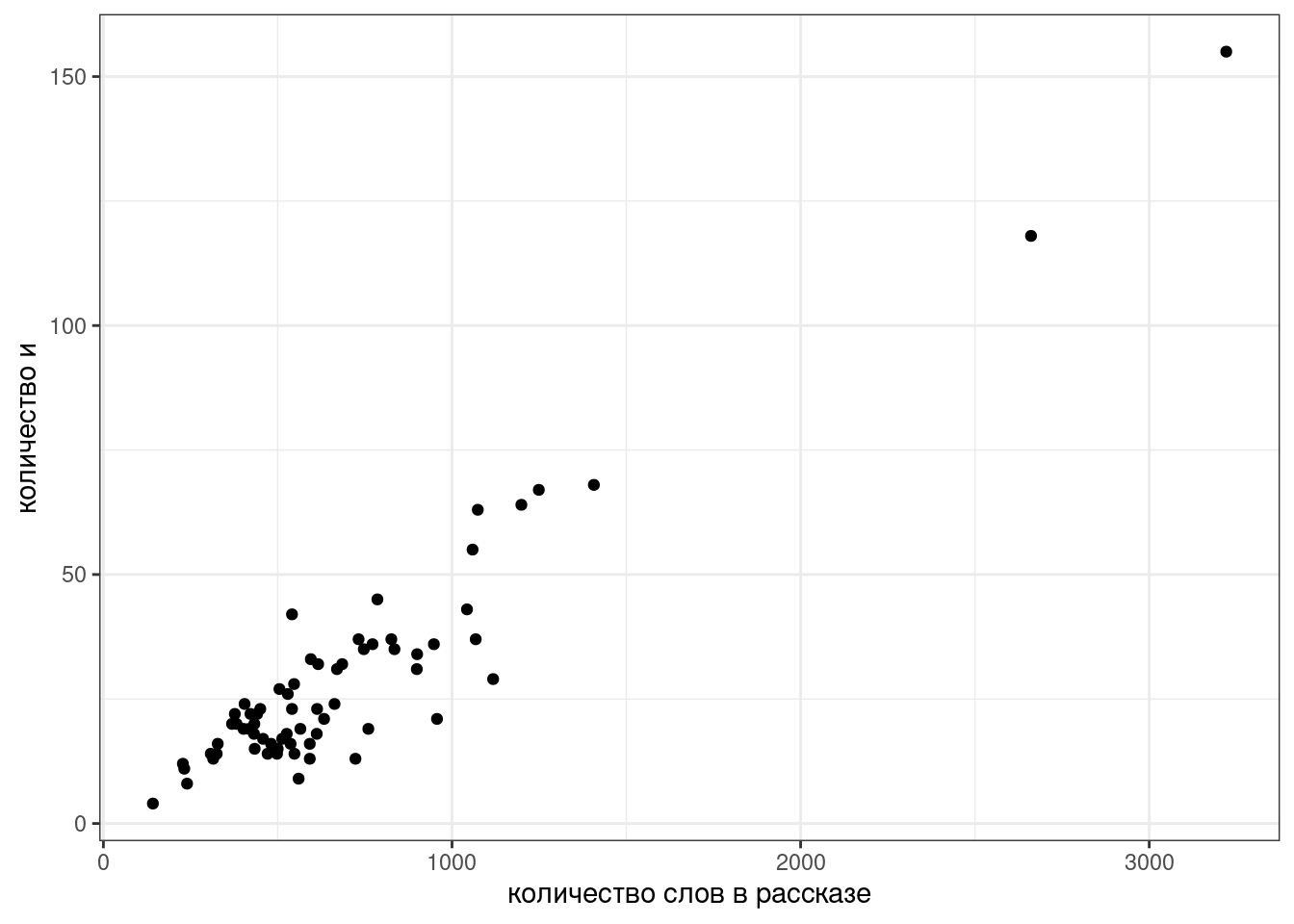

Мы видим, несколько одиночных точек, давайте избавимся от них и добавим регрессионную линию при помощи функции geom_smooth():

zo %>% 
  filter(word == "и",
         n_words < 1500) %>% 
  distinct() ->
  zo_filtered

zo_filtered %>%   
  ggplot(aes(n_words, n))+
  geom_point()+
  geom_smooth(method = "lm", se = FALSE)+
  labs(x = "количество слов в рассказе",
       y = "количество и")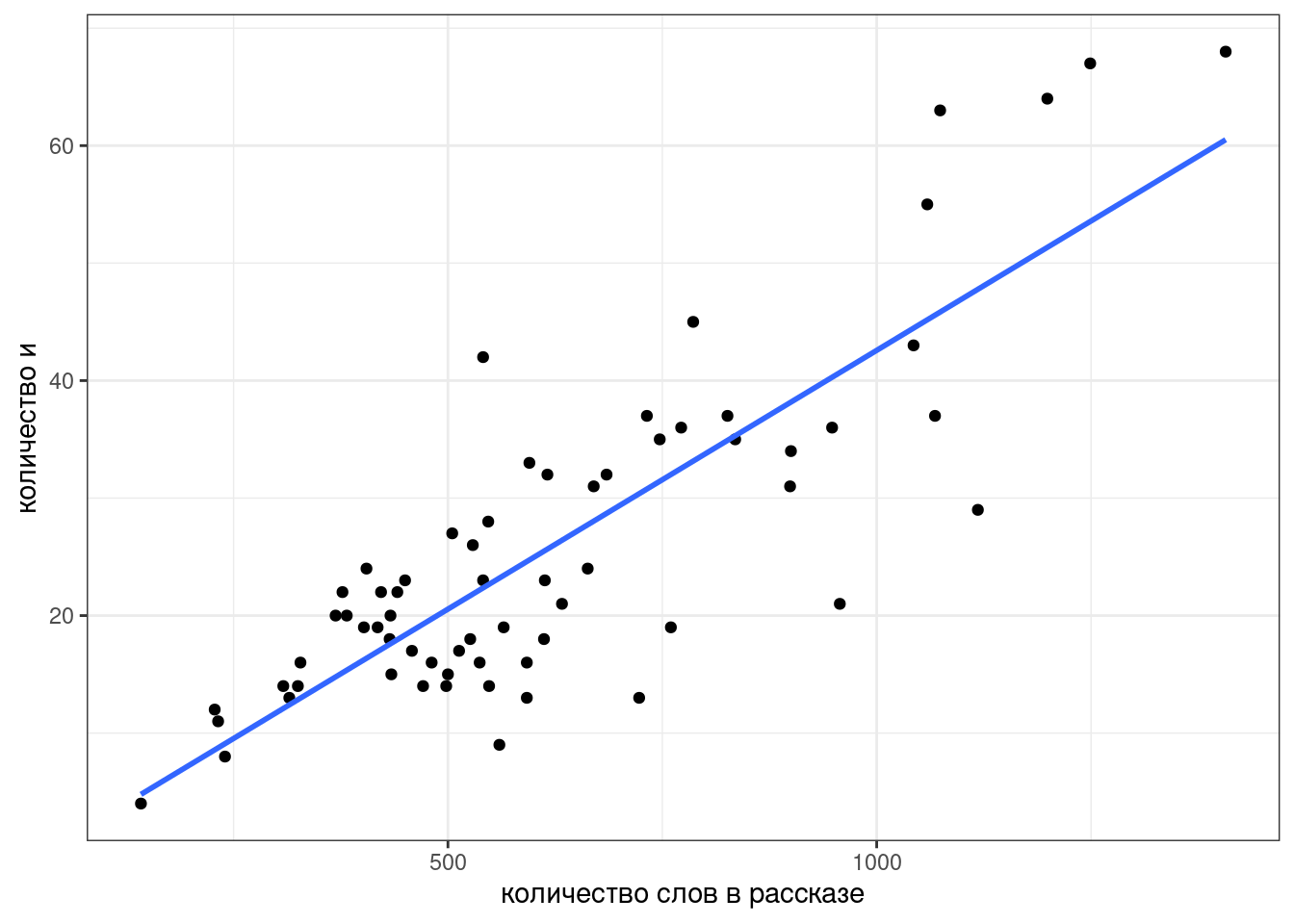

Чтобы получить формулу этой линии нужно запустить функцию, которая оценивает линейную регрессию:

fit <- lm(n~n_words, data = zo_filtered)
fit

Call:
lm(formula = n ~ n_words, data = zo_filtered)

Coefficients:
(Intercept)      n_words  
   -1.47184      0.04405  

Вот мы и получили коэффициенты, теперь мы видим, что наша модель считает следующее:

\[n = -1.47184 + 0.04405 \times n\_words\]

Более подробную информцию можно посмотреть, если запустить модель в функцию summary():

summary(fit)

Call:
lm(formula = n ~ n_words, data = zo_filtered)

Residuals:
     Min       1Q   Median       3Q      Max 
-19.6830  -4.3835   0.8986   4.6486  19.6413 

Coefficients:
             Estimate Std. Error t value            Pr(>|t|)    
(Intercept) -1.471840   2.467149  -0.597               0.553    
n_words      0.044049   0.003666  12.015 <0.0000000000000002 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 7.945 on 64 degrees of freedom
Multiple R-squared:  0.6928,    Adjusted R-squared:  0.688 
F-statistic: 144.4 on 1 and 64 DF,  p-value: < 0.00000000000000022

В разделе Coefficients содержится информацию про наши коэффициенты:

• Estimate – полученная оценка коэффициентов;
• Std. Error – стандартная ошибка среднего;
• t value – \(t\)-статистика, полученная при проведении одновыборочного \(t\)-теста, сравнивающего данный коэфициент с 0;
• Pr(>|t|) – полученное \(p\)-значение;
• Multiple R-squared и Adjusted R-squared — одна из оценок модели, показывает связь между переменными. Без поправок совпадает с квадратом коэффициента корреляции Пирсона:

cor(zo_filtered$n_words, zo_filtered$n)^2

[1] 0.6928376

• F-statistic — \(F\)-статистика полученная при проведении теста, проверяющего, не являются ли хотя бы один из коэффицинтов статистически значимо отличается от нуля. Совпадает с результатами дисперсионного анализа (ANOVA).

Теперь мы можем даже предсказывать значения, которые мы еще не видели. Например, сколько будет и в рассказе Зощенко длиной 1000 слов?

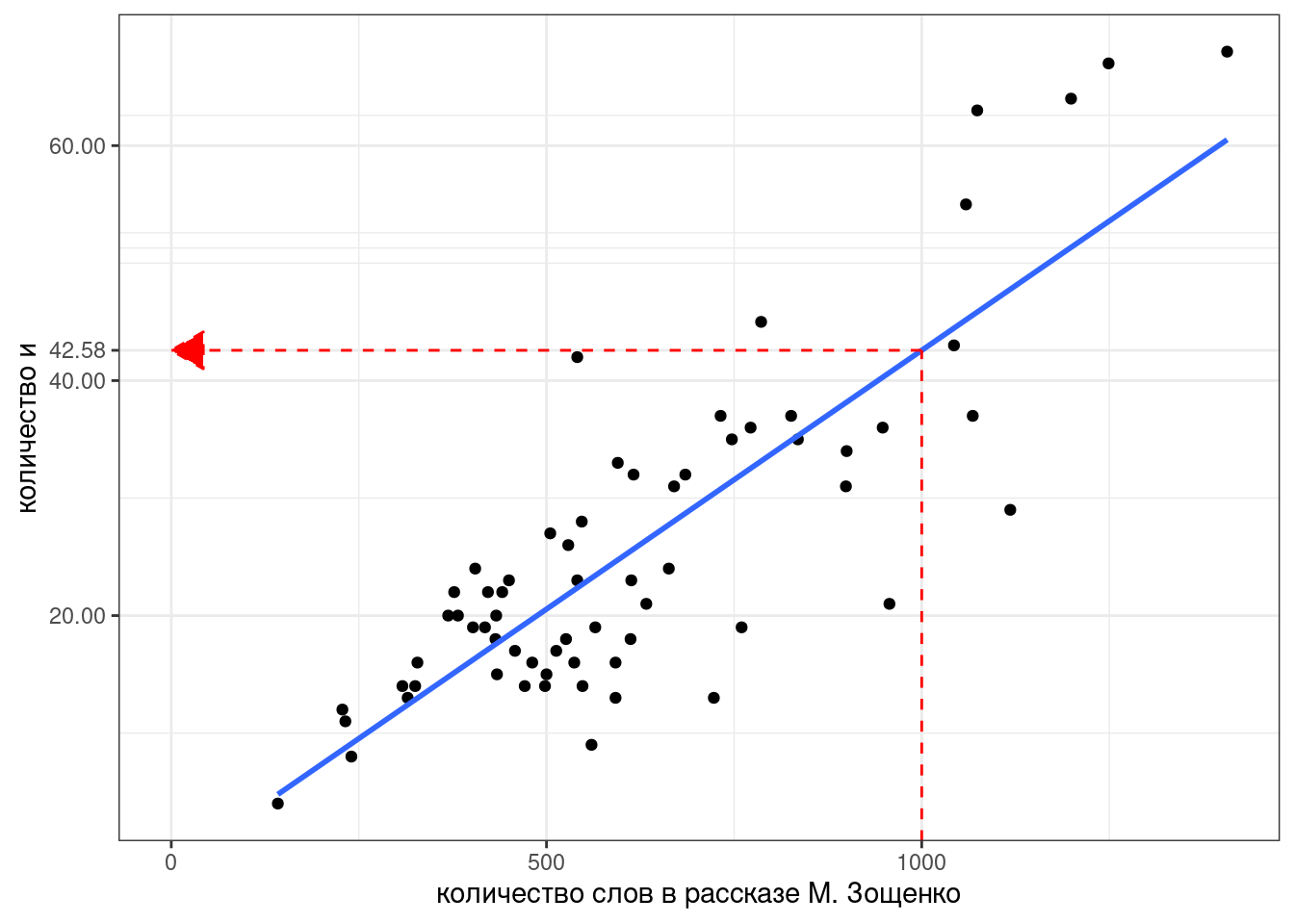
predict(fit, tibble(n_words = 1000))

       1 
42.57715 

10.4.2 Категориальные переменные

Что если мы хотим включить в наш анализ категориальные переменные? Давайте рассмотрим простой пример с рассказами Чехова и Зощенко, которые мы рассматривали в прошлом разделе. Мы будем анализировать логарифм доли слов деньги:

chekhov <- read_tsv("https://github.com/agricolamz/DS_for_DH/raw/master/data/tidy_chekhov.tsv")
zoshenko <- read_tsv("https://github.com/agricolamz/DS_for_DH/raw/master/data/tidy_zoshenko.csv")

chekhov$author <- "Чехов"
zoshenko$author <- "Зощенко"

chekhov %>% 
  bind_rows(zoshenko) %>% 
  filter(str_detect(word, "деньг")) %>% 
  group_by(author, titles, n_words) %>% 
  summarise(n = sum(n)) %>% 
  mutate(log_ratio = log(n/n_words)) ->
  checkov_zoshenko

Визуализация выглядит так:

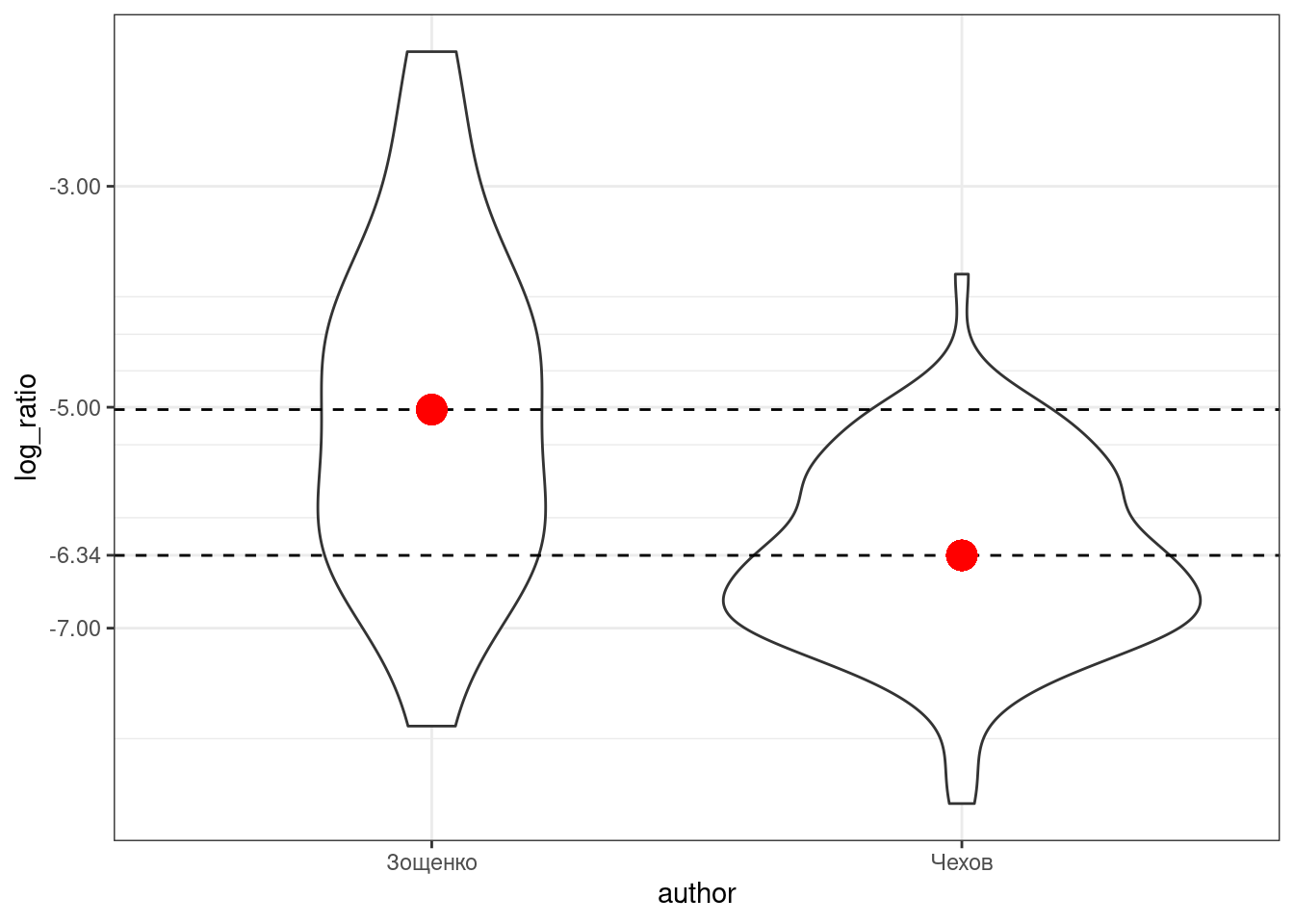
Красной точкой обозначены средние значения, так что мы видим, что между двумя писателями есть разница, но является ли она статистически значимой? В прошлом разделе, мы рассмотрели, что в таком случае можно сделать t-test:

t.test(log_ratio~author, 
       data = checkov_zoshenko, 
       var.equal =TRUE) # здесь я мухлюю, отключая поправку Уэлча

    Two Sample t-test

data:  log_ratio by author
t = 5.6871, df = 125, p-value = 0.00000008665
alternative hypothesis: true difference in means between group Зощенко and group Чехов is not equal to 0
95 percent confidence interval:
 0.8606107 1.7793181
sample estimates:
mean in group Зощенко   mean in group Чехов 
            -5.021262             -6.341226 

Разница между группами является статистически значимой (t(125) = 5.6871, p-value = 8.665e-08).

Для того, чтобы запустить регрессию на категориальных данных категориальная переменная автоматически разбивается на группу бинарных dummy-переменных:

tibble(author = c("Чехов", "Зощенко"),
       dummy_chekhov = c(1, 0),
       dummy_zoshenko = c(0, 1))

Дальше для регрессионного анализа выкидывают одну из переменных, так как иначе модель не сойдется (dummy-переменных всегда n-1, где n — количество категорий в переменной).

tibble(author = c("Чехов", "Зощенко"),
       dummy_chekhov = c(1, 0))

Если переменная dummy_chekhov принимает значение 1, значит речь о рассказе Чехова, а если принимает значение 0, то о рассказе Зощенко. Если вставить нашу переменную в регрессионную формулу получится следующее:

\[y_i = \hat\beta_0 + \hat\beta_1 \times \text{dummy_chekhov} + \epsilon_i,\]

Так как dummy_chekhov принимает либо значение 1, либо значение 0, то получается, что модель предсказывает лишь два значения:

\[y_i = \left\{\begin{array}{ll}\hat\beta_0 + \hat\beta_1 \times 1 + \epsilon_i = \hat\beta_0 + \hat\beta_1 + \epsilon_i\text{, если рассказ Чехова}\\ \hat\beta_0 + \hat\beta_1 \times 0 + \epsilon_i = \hat\beta_0 + \epsilon_i\text{, если рассказ Зощенко} \end{array}\right.\]

Таким образом, получается, что свободный член \(\beta_0\) и угловой коэффициент \(\beta_1\) в регресси с категориальной переменной получает другую интерпретацию. Одно из значений переменной кодируется при помощи \(\beta_0\), а сумма коэффициентов \(\beta_0+\beta_1\) дают другое значение переменной. Так что \(\beta_1\) — это разница между оценками двух значений переменной.

Давайте теперь запустим регрессию на этих же данных:

fit2 <- lm(log_ratio~author, data = checkov_zoshenko)
summary(fit2)

Call:
lm(formula = log_ratio ~ author, data = checkov_zoshenko)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.8652 -0.6105 -0.0607  0.6546  3.2398 

Coefficients:
            Estimate Std. Error t value             Pr(>|t|)    
(Intercept)  -5.0213     0.2120 -23.680 < 0.0000000000000002 ***
authorЧехов  -1.3200     0.2321  -5.687         0.0000000867 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.9717 on 125 degrees of freedom
Multiple R-squared:  0.2056,    Adjusted R-squared:  0.1992 
F-statistic: 32.34 on 1 and 125 DF,  p-value: 0.00000008665

Во-первых стоит обратить внимание на то, что R сам преобразовал нашу категориальную переменную в dummy-переменную authorЧехов. Во-вторых, можно заметить, что значения t-статистики и p-value совпадают с результатами полученными нами в t-тесте выше. Статистическти значимый коэффициент при аргументе authorЧехов следует интерпретировать как разницу средних между логарифмом долей в рассказах Чехова и Зощенко.

10.4.3 Множественная регрессия

Множественная регрессия позволяет проанализировать связь между зависимой и несколькими зависимыми переменными. Формула множественной регрессии не сильно отличается от формулы обычной линейной регрессии:

\[y_i = \hat\beta_0 + \hat\beta_1 \times x_{1i}+ \dots+ \hat\beta_n \times x_{ni} + \epsilon_i,\]

• \(x_{ki}\) — \(i\)-ый элемент векторов значений \(X_1, \dots, X_n\);
• \(y_i\) — \(i\)-ый элемент вектора значений \(Y\);
• \(\hat\beta_0\) — оценка случайного члена (intercept);
• \(\hat\beta_k\) — коэфциент при переменной \(X_{k}\);
• \(\epsilon_i\) — \(i\)-ый остаток, разница между оценкой модели (\(\hat\beta_0 + \hat\beta_1 \times x_i\)) и реальным значением \(y_i\); весь вектор остатков иногда называют случайным шумом.

В такой регресии предикторы могут быть как числовыми, так и категориальными (со всеми вытекающими последствиями, которые мы обсудили в предудщем разделе). Такую регрессию чаще всего сложно визуализировать, так как в одну регрессионную линию вкладываются сразу несколько переменных.

Попробуем предсказать длину лепестка на основе длины чашелистик и вида ириса:

iris %>% 
  ggplot(aes(Sepal.Length, Petal.Length, color = Species))+
  geom_point()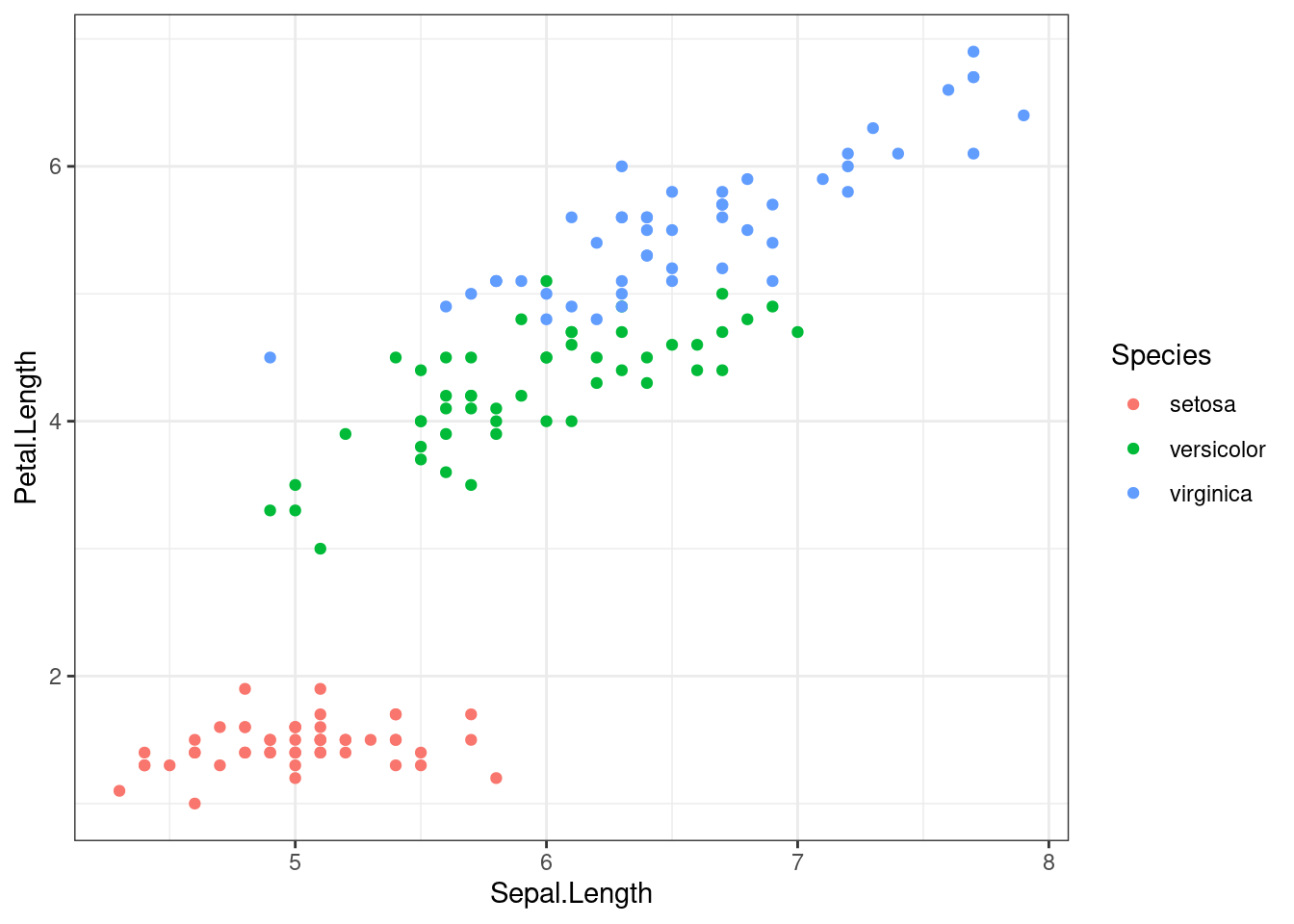

Запустим регрессию:

fit3 <- lm(Petal.Length ~ Sepal.Length+ Species, data = iris)
summary(fit3)

Call:
lm(formula = Petal.Length ~ Sepal.Length + Species, data = iris)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.76390 -0.17875  0.00716  0.17461  0.79954 

Coefficients:
                  Estimate Std. Error t value             Pr(>|t|)    
(Intercept)       -1.70234    0.23013  -7.397      0.0000000000101 ***
Sepal.Length       0.63211    0.04527  13.962 < 0.0000000000000002 ***
Speciesversicolor  2.21014    0.07047  31.362 < 0.0000000000000002 ***
Speciesvirginica   3.09000    0.09123  33.870 < 0.0000000000000002 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.2826 on 146 degrees of freedom
Multiple R-squared:  0.9749,    Adjusted R-squared:  0.9744 
F-statistic:  1890 on 3 and 146 DF,  p-value: < 0.00000000000000022

Все предикторы статистически значимы. Давайте посмотрим предсказания модели для всех наблюдений:

iris %>% 
  mutate(prediction = predict(fit3)) %>% 
  ggplot(aes(Sepal.Length, prediction, color = Species))+
  geom_point()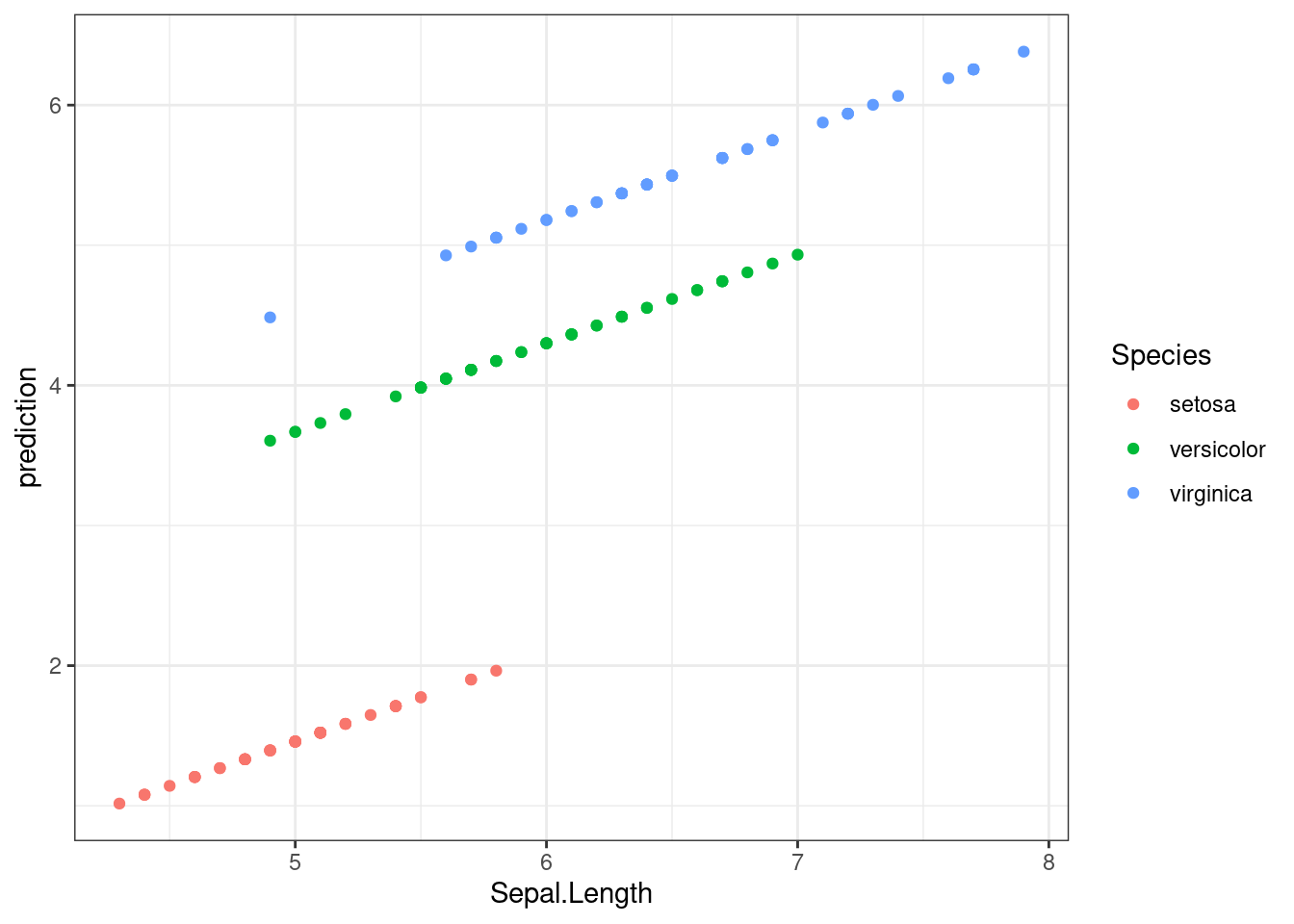

Всегда имеет смысл визуализировать, что нам говорит наша модель. Если использовать пакет ggeffects (или предшествовавший ему пакет effects), это можно сделать не сильно задумываясь, как это делать:

library(ggeffects)
plot(ggpredict(fit3, terms = c("Sepal.Length", "Species")))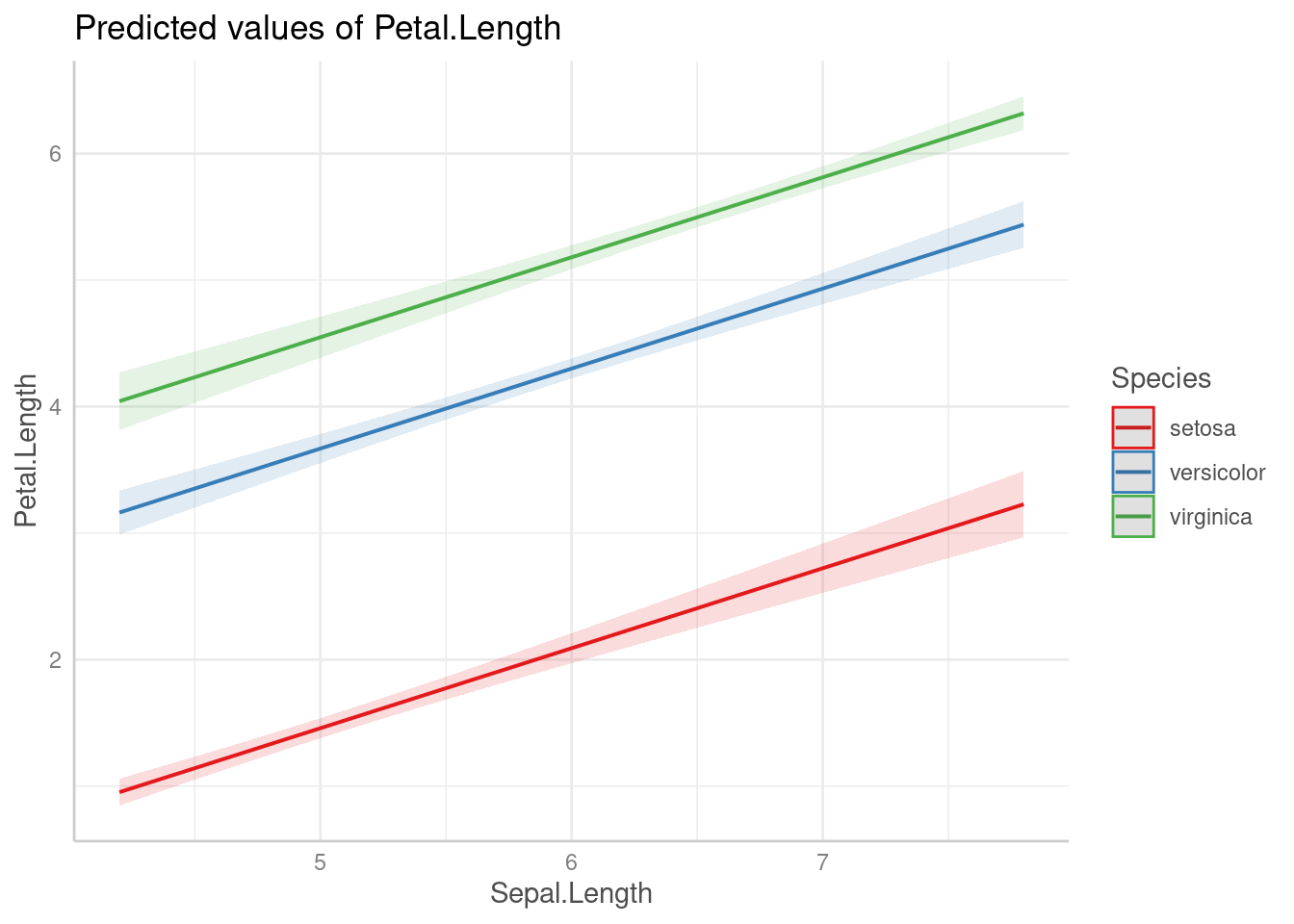

Как видно из графиков, наша модель имеет одинаковые угловые коэффициенты (slope) для каждого из видов ириса и разные свободные члены (intercept).

summary(fit3)

Call:
lm(formula = Petal.Length ~ Sepal.Length + Species, data = iris)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.76390 -0.17875  0.00716  0.17461  0.79954 

Coefficients:
                  Estimate Std. Error t value             Pr(>|t|)    
(Intercept)       -1.70234    0.23013  -7.397      0.0000000000101 ***
Sepal.Length       0.63211    0.04527  13.962 < 0.0000000000000002 ***
Speciesversicolor  2.21014    0.07047  31.362 < 0.0000000000000002 ***
Speciesvirginica   3.09000    0.09123  33.870 < 0.0000000000000002 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.2826 on 146 degrees of freedom
Multiple R-squared:  0.9749,    Adjusted R-squared:  0.9744 
F-statistic:  1890 on 3 and 146 DF,  p-value: < 0.00000000000000022

\[y_i = \left\{\begin{array}{ll} -1.70234 + 0.63211 \times \text{Sepal.Length} + \epsilon_i\text{, если вид setosa}\\ -1.70234 + 2.2101 + 0.63211 \times \text{Sepal.Length} + \epsilon_i\text{, если вид versicolor} \\ -1.70234 + 3.09 + 0.63211 \times \text{Sepal.Length} + \epsilon_i\text{, если вид virginica} \end{array}\right.\]

10.5 Нелинейность взаимосвязи

Давайте восползуемся данными из пакета Rling Натальи Левшиной. В датасете 100 произвольно выбранных слов из проекта English Lexicon Project (Balota et al. 2007), их длина, среднее время реакции и частота в корпусе.

ldt <- read_csv("https://goo.gl/ToxfU6")
ldt

Давайте посмотрим на простой график:

ldt %>% 
  ggplot(aes(Mean_RT, Freq))+
  geom_point()+
  theme_bw()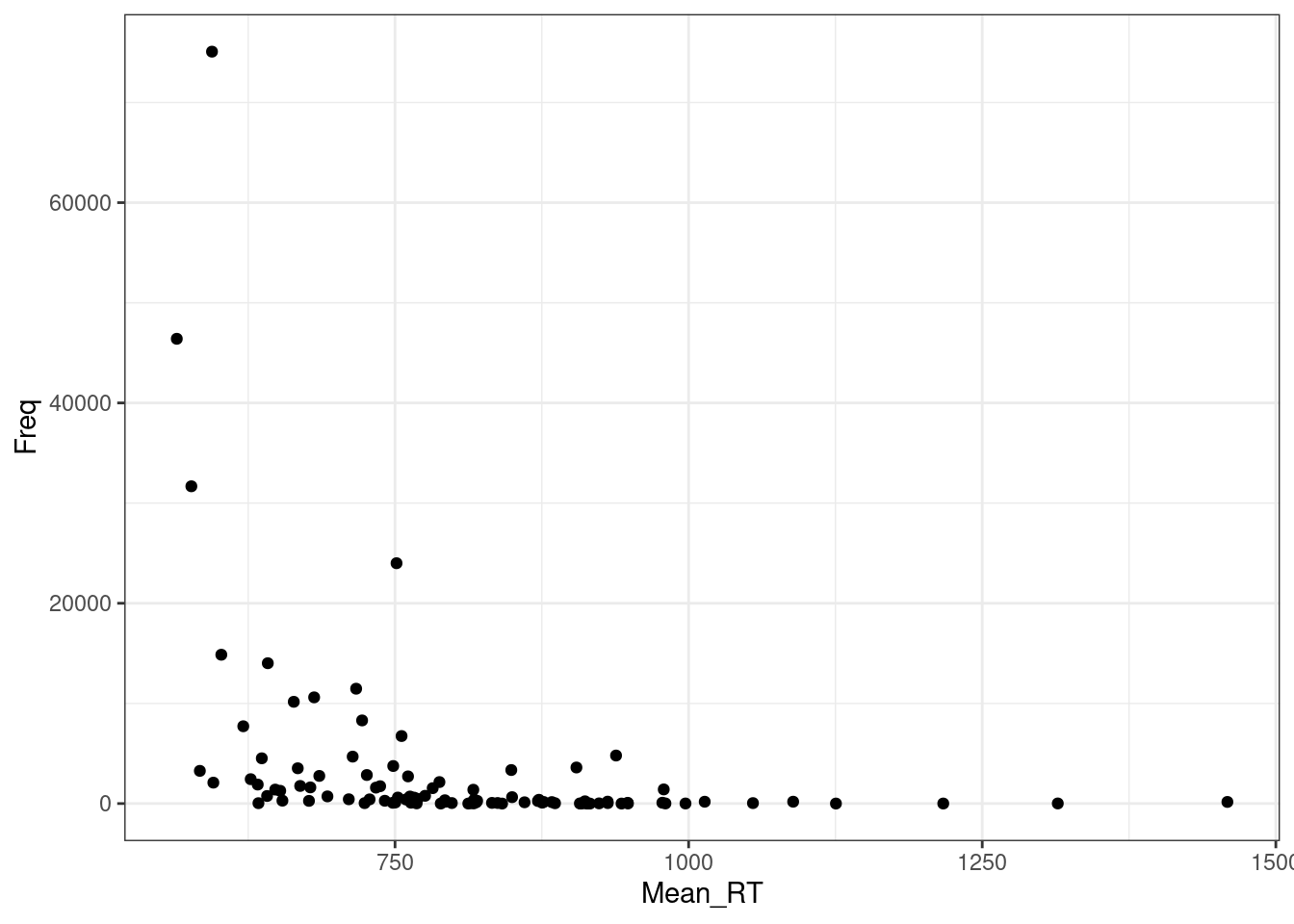

Регрессия на таких данных будет супер неиформативна:

ldt %>% 
  ggplot(aes(Mean_RT, Freq))+
  geom_point()+
  geom_smooth(method = "lm")+
  theme_bw()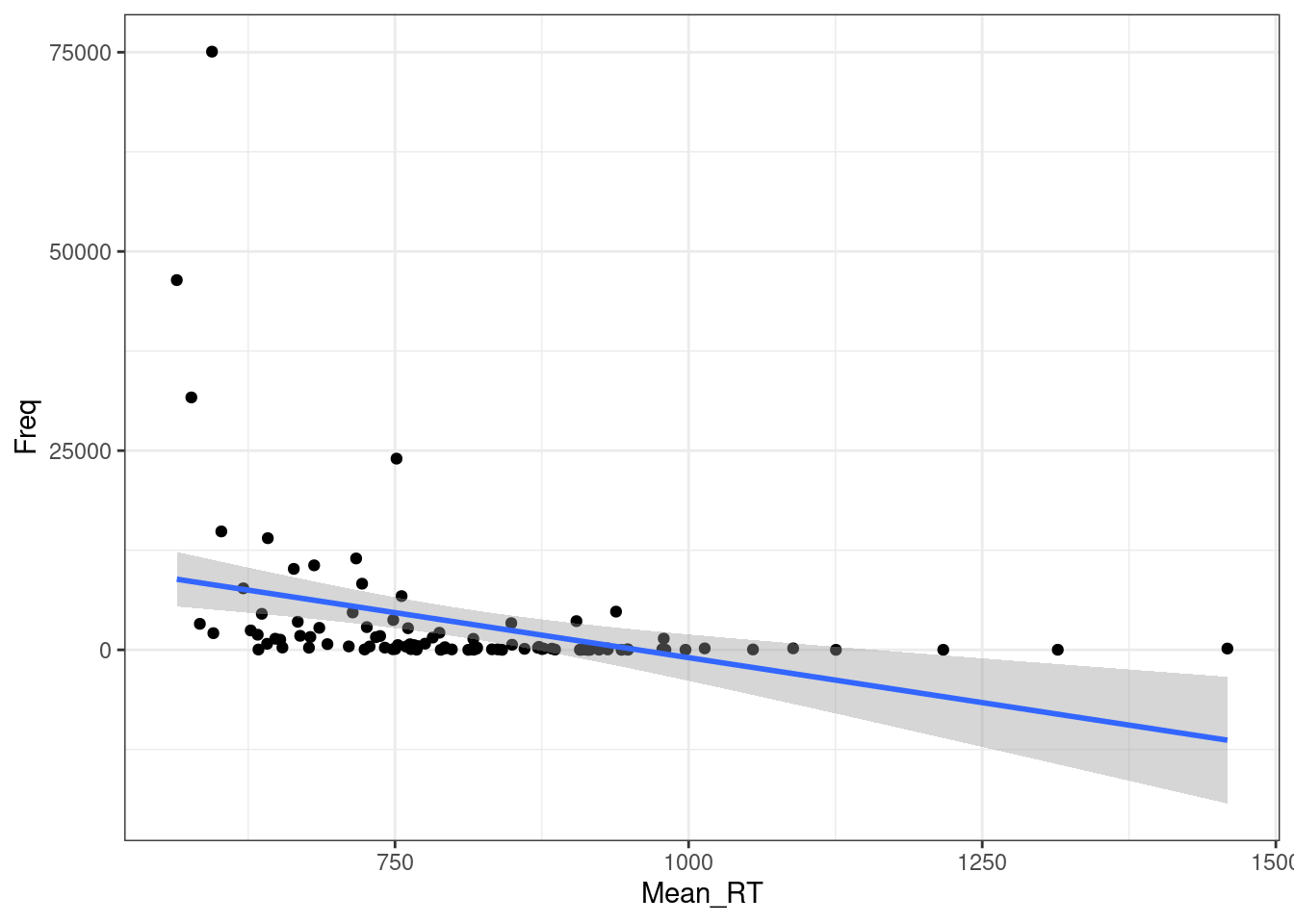

m1 <- summary(lm(Mean_RT~Freq, data = ldt))
m1

Call:
lm(formula = Mean_RT ~ Freq, data = ldt)

Residuals:
    Min      1Q  Median      3Q     Max 
-224.93  -85.42  -30.52   81.90  632.66 

Coefficients:
              Estimate Std. Error t value             Pr(>|t|)    
(Intercept) 826.998242  15.229783  54.301 < 0.0000000000000002 ***
Freq         -0.005595   0.001486  -3.765             0.000284 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 143.9 on 98 degrees of freedom
Multiple R-squared:  0.1264,    Adjusted R-squared:  0.1174 
F-statistic: 14.17 on 1 and 98 DF,  p-value: 0.0002843

10.5.1 Логарифмирование

ldt %>% 
  ggplot(aes(Mean_RT, log(Freq)))+
  geom_point()+
  geom_smooth(method = "lm")+
  theme_bw()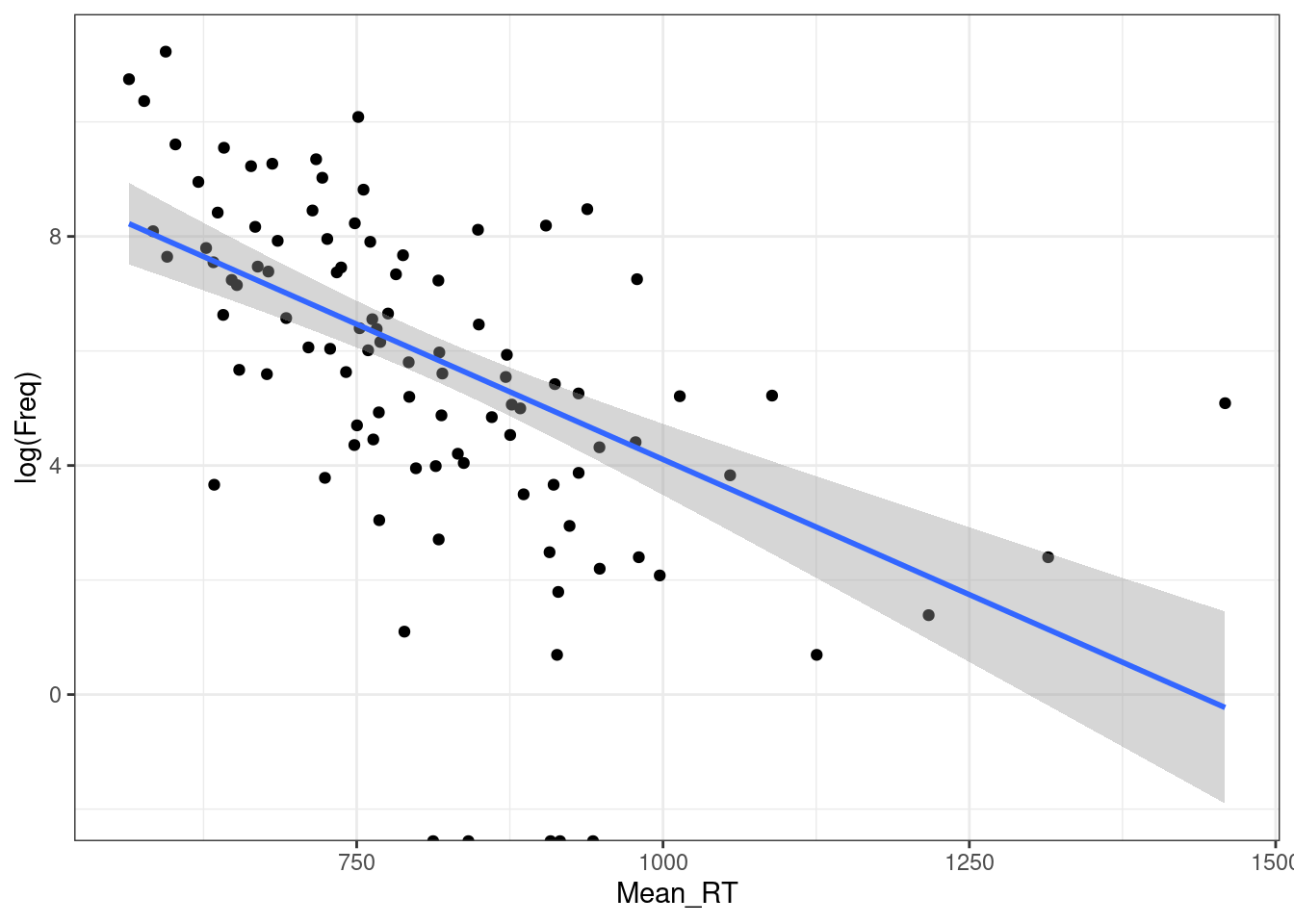

ldt %>% 
  ggplot(aes(Mean_RT, log(Freq+1)))+
  geom_point()+
  geom_smooth(method = "lm")+
  theme_bw()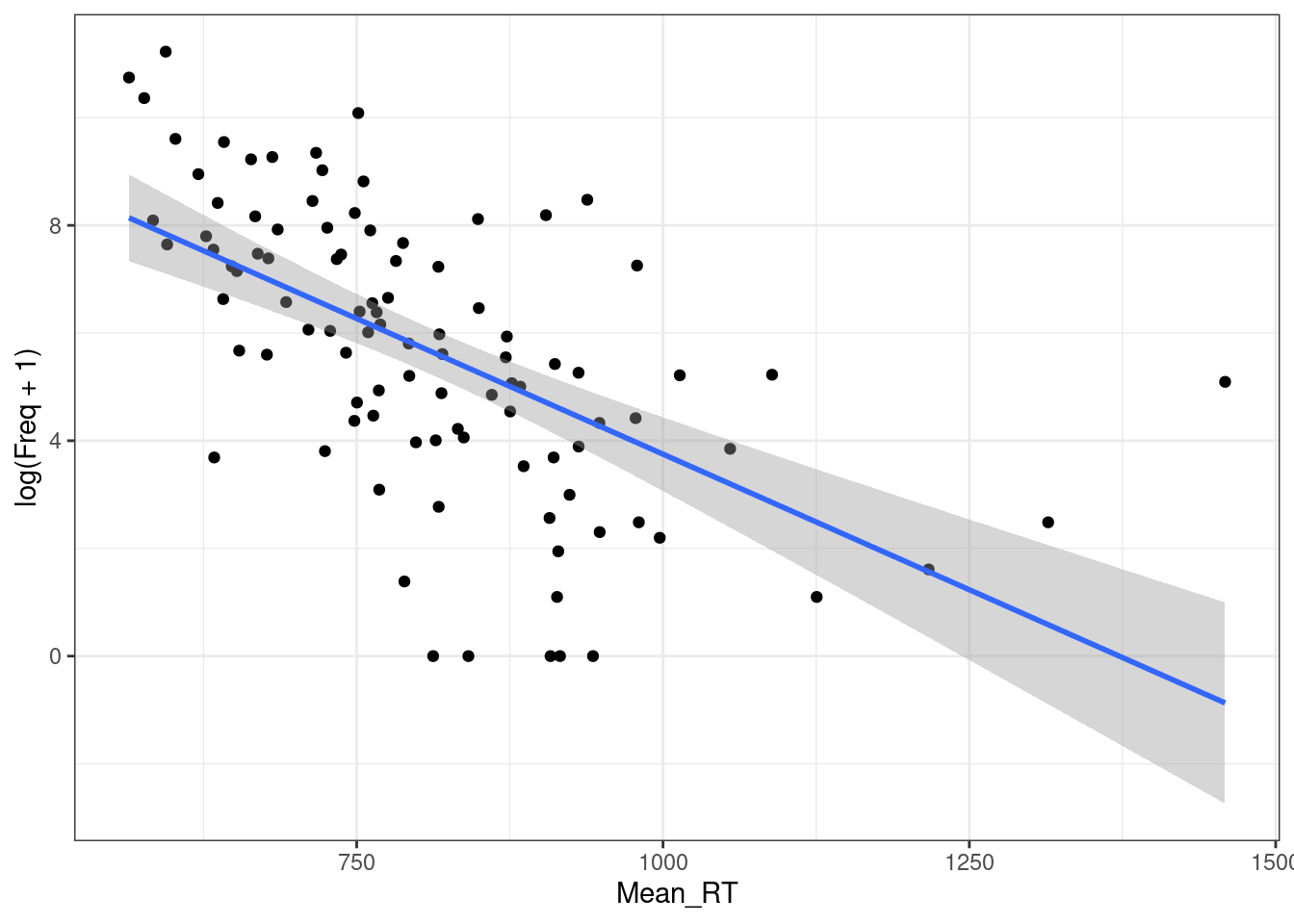

m2 <- summary(lm(Mean_RT~log(Freq+1), data = ldt))
m2

Call:
lm(formula = Mean_RT ~ log(Freq + 1), data = ldt)

Residuals:
    Min      1Q  Median      3Q     Max 
-242.36  -76.66  -17.49   48.64  630.49 

Coefficients:
              Estimate Std. Error t value             Pr(>|t|)    
(Intercept)    1001.60      29.79  33.627 < 0.0000000000000002 ***
log(Freq + 1)   -34.03       4.76  -7.149       0.000000000158 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 124.8 on 98 degrees of freedom
Multiple R-squared:  0.3428,    Adjusted R-squared:  0.3361 
F-statistic: 51.11 on 1 and 98 DF,  p-value: 0.0000000001576

m1$adj.r.squared

[1] 0.1174405

m2$adj.r.squared

[1] 0.336078

Отлогорифмировать можно и другую переменную.

ldt %>% 
  ggplot(aes(log(Mean_RT), log(Freq  + 1)))+
  geom_point()+
  geom_smooth(method = "lm")+
  theme_bw()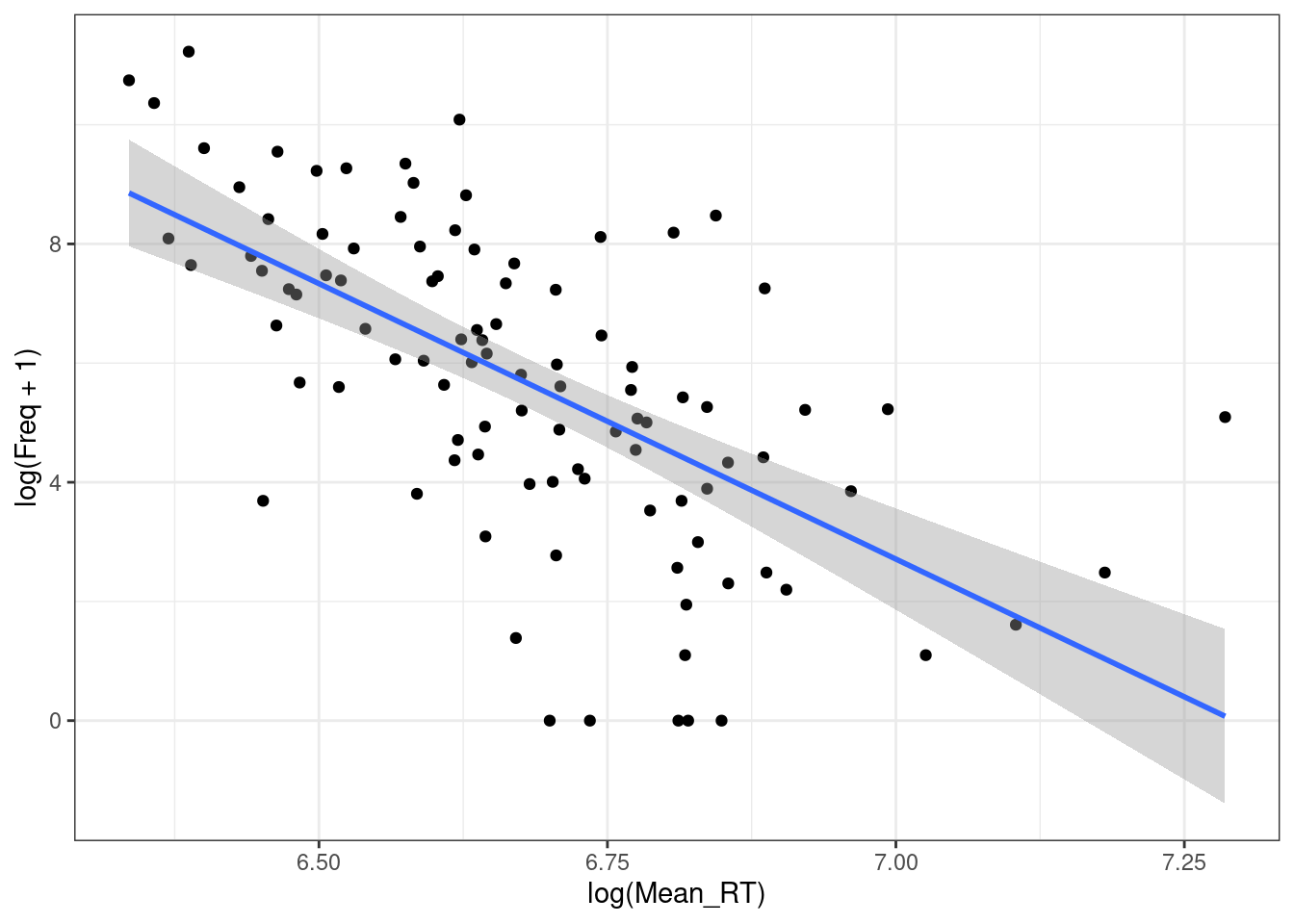

m3 <- summary(lm(log(Mean_RT)~log(Freq+1), data = ldt))
m1$adj.r.squared

[1] 0.1174405

m2$adj.r.squared

[1] 0.336078

m3$adj.r.squared

[1] 0.3838649

Как интерпретировать полученную регрессию с двумя отлогорифмированными значениями?

В обычной линейной регресии мы узнаем отношения между \(x\) и \(y\): \[y_i = \beta_0+\beta_1\times x_i\]

Как изменится \(y_j\), если мы увеличем \(x_i + 1 = x_j\)? \[y_j = \beta_0+\beta_1\times x_j\]

\[y_j - y_i = \beta_0+\beta_1\times x_j - (\beta_0+\beta_1\times x_i) = \beta_1(x_j - x_i)\]

Т. е. \(y\) увеличится на \(\beta_1\) , если \(x\) увеличится на 1. Что же будет с логарифмированными переменными? Как изменится \(y_j\), если мы увеличем \(x_i + 1 = x_j\)?

\[\log(y_j) - \log(y_i) = \beta_1\times (\log(x_j) - \log(x_i))\]

\[\log\left(\frac{y_j}{y_i}\right) = \beta_1\times \log\left(\frac{x_j}{x_i}\right) = \log\left(\left(\frac{x_j}{x_i}\right) ^ {\beta_1}\right)\]

\[\frac{y_j}{y_i}= \left(\frac{x_j}{x_i}\right) ^ {\beta_1}\]

Т. е. \(y\) увеличится на \(\beta_1\) процентов, если \(x\) увеличится на 1 процент.

Логарифмирование — не единственный вид траснформации:

• трансформация Тьюки

shiny::runGitHub("agricolamz/tukey_transform")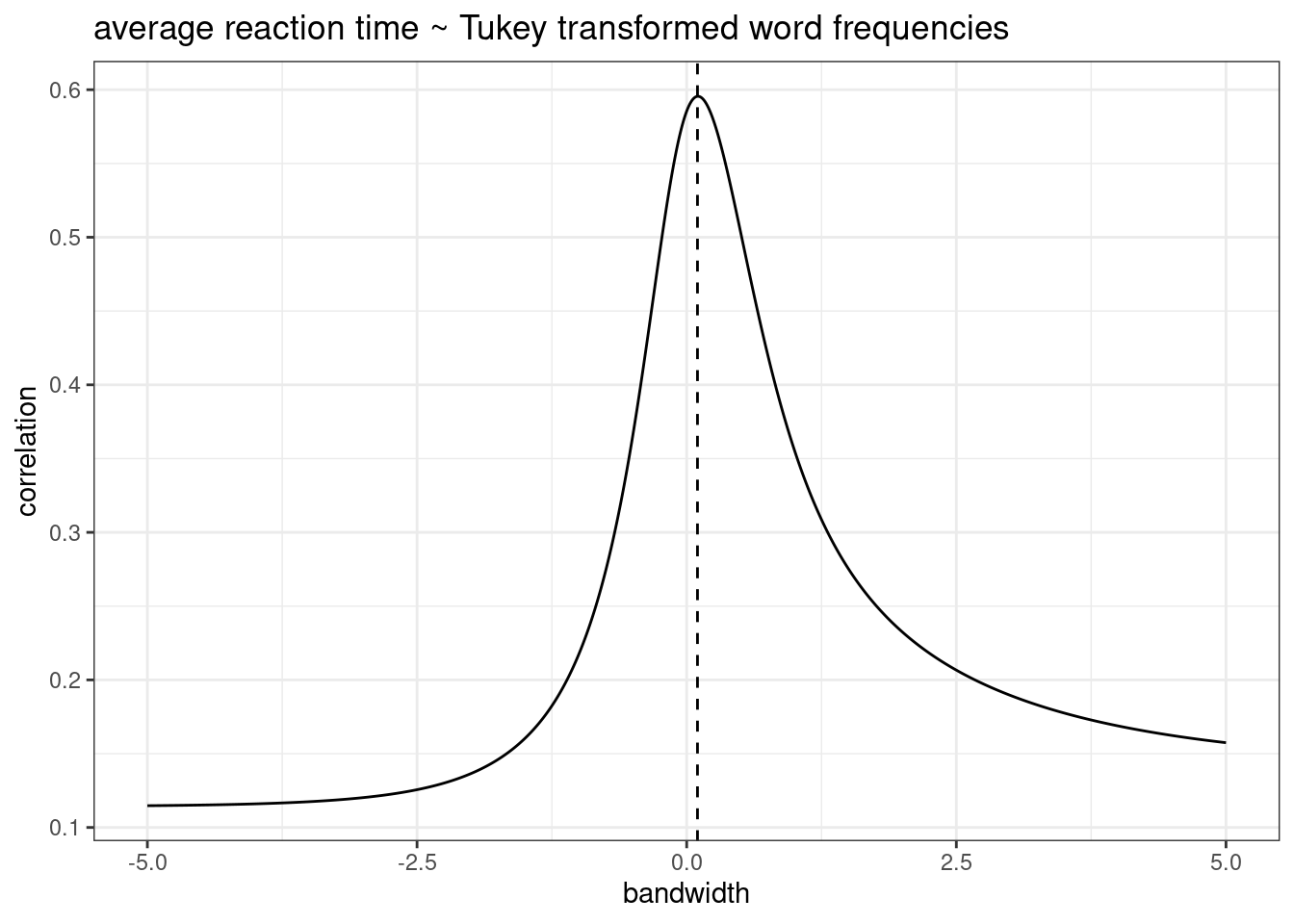

• трансформация Бокса — Кокса
• …

В датасет собрана частотность разных лемм на основании корпуса НКРЯ (Ляшевская and Шаров 2009) (в датасете только значения больше ipm > 10). Известно, что частотность слова связана с рангом слова (см. закон Ципфа). Постройте переменную ранга и визуализируйте связь ранга и логорифма частотности с разбивкой по частям речи. Какие части речи так и не приобрели после трансформации “приемлимую” линейную форму? (я насчитал 5 таких)

a
adv
advpro
anum
apro
conj
intj
num
part
pr
s
s.PROP
spro
v

10.6 Нормальность распределение остатков

Линейная регрессия предполагает нормальность распределения остатков. Когда связь не линейна, то остатки тоже будут распределены не нормально.

Можно смотреть на первый график используя функцию plot(m1) — график остатков. Интерпретаций этого графика достаточно много (см. статью про это).

Можно смотреть на qqplot:

tibble(res = m1$residuals) %>% 
  ggplot(aes(res))+
  geom_histogram(aes(y = ..density..))+
  stat_function(fun = dnorm, args = list(mean = 0, sd = sd(m1$residuals)), color = "red")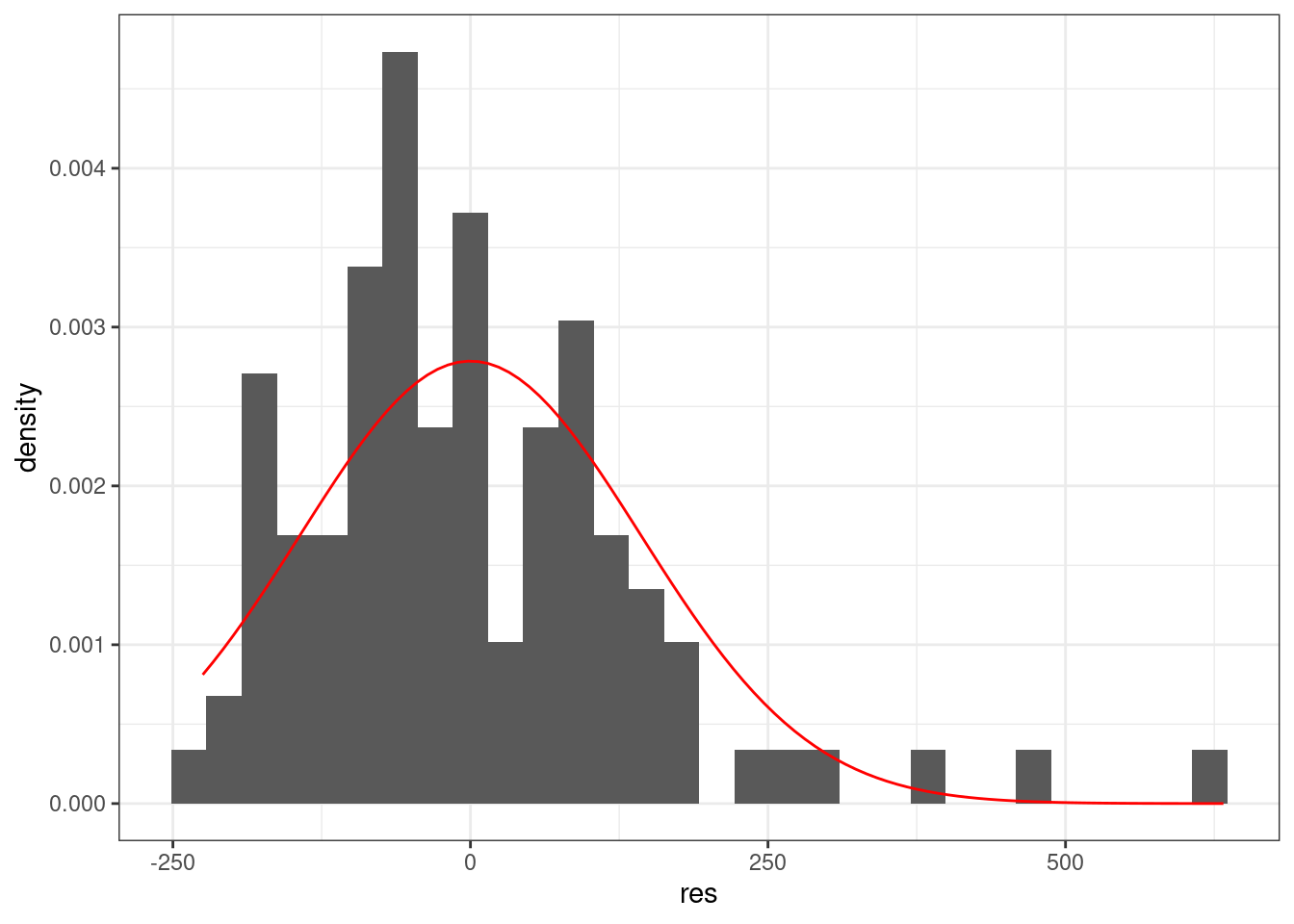

qqnorm(m1$residuals)
qqline(m1$residuals)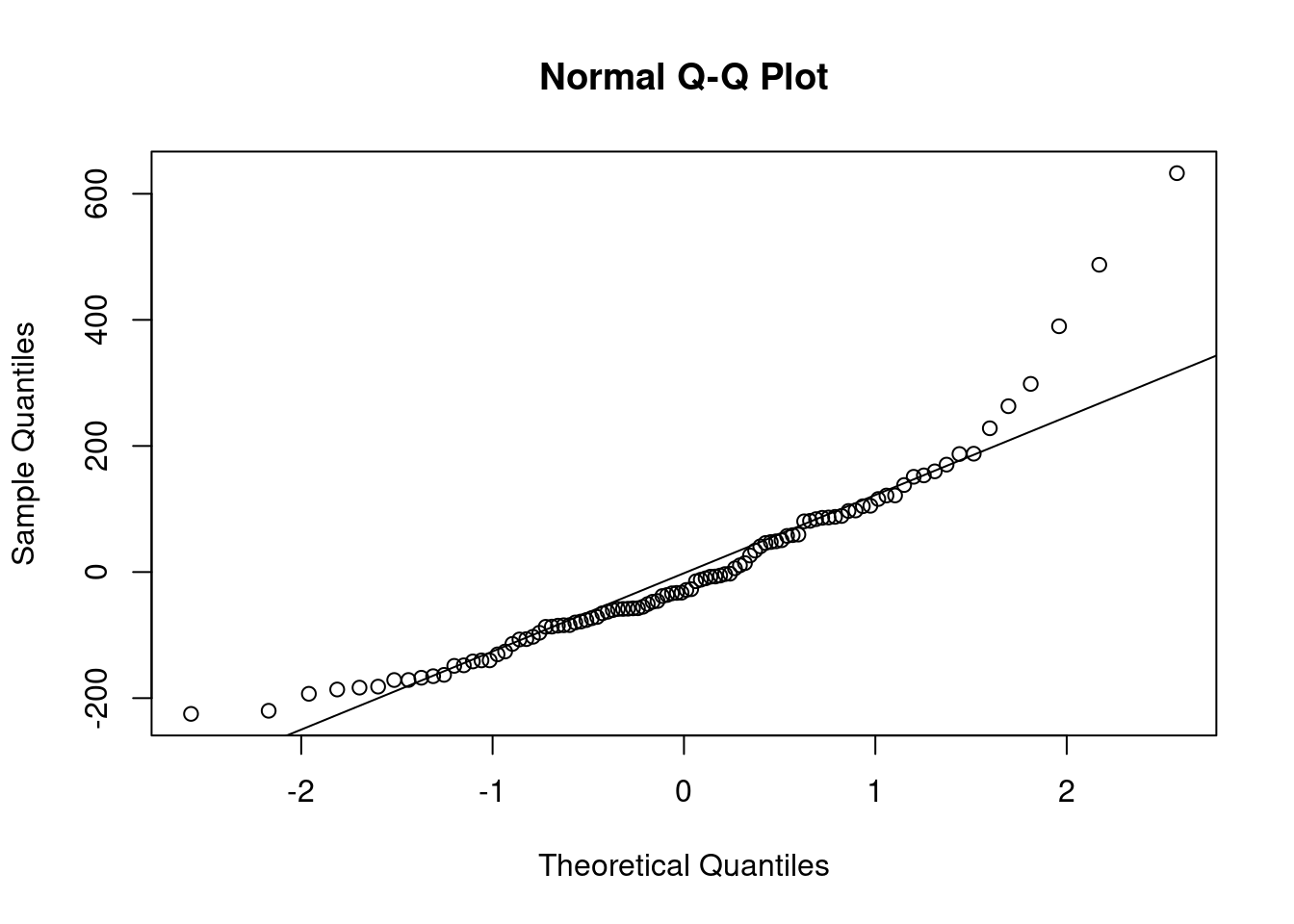

tibble(res = m2$residuals) %>% 
  ggplot(aes(res))+
  geom_histogram(aes(y = ..density..))+
  stat_function(fun = dnorm, args = list(mean = 0, sd = sd(m2$residuals)), color = "red")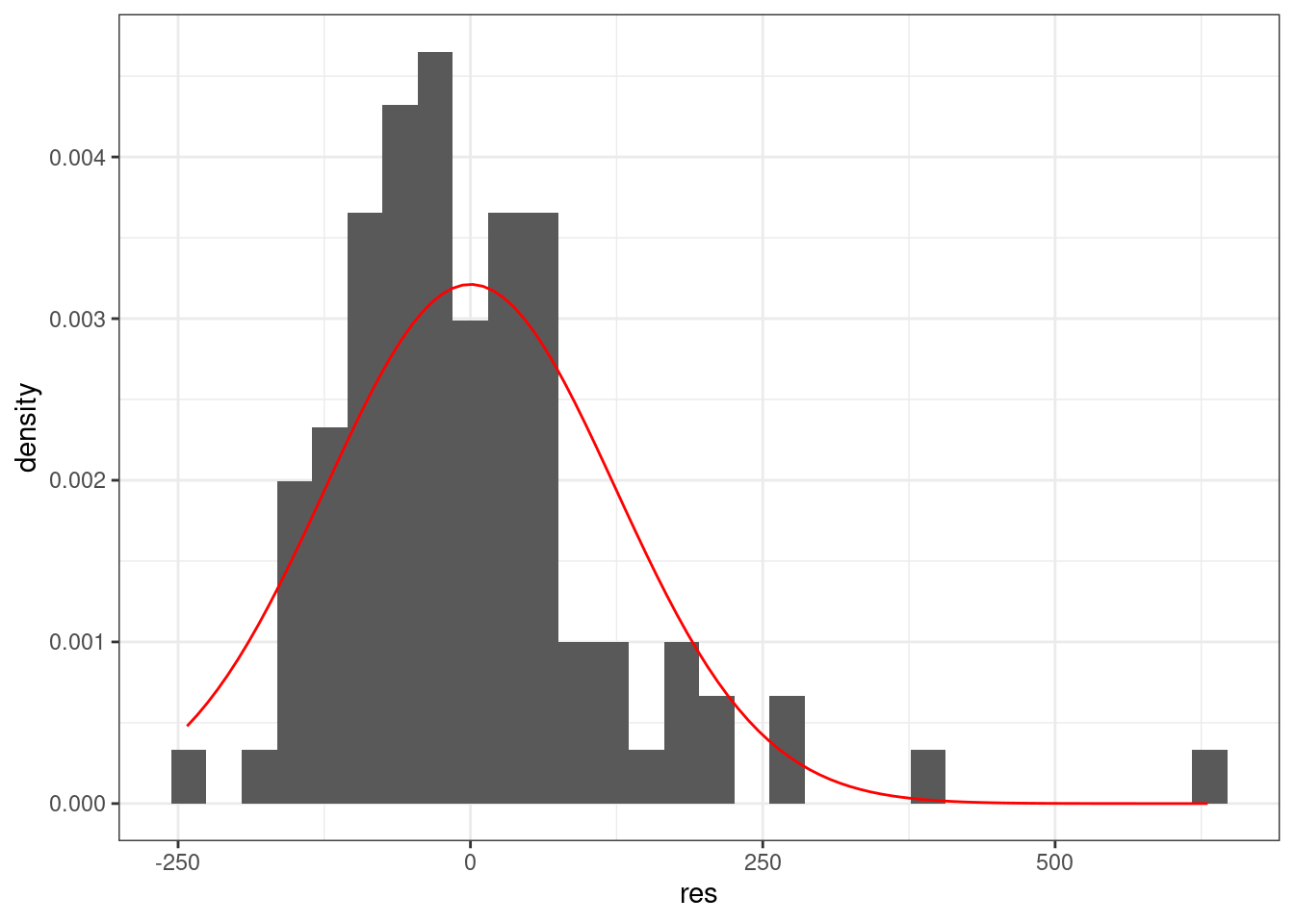

qqnorm(m2$residuals)
qqline(m2$residuals)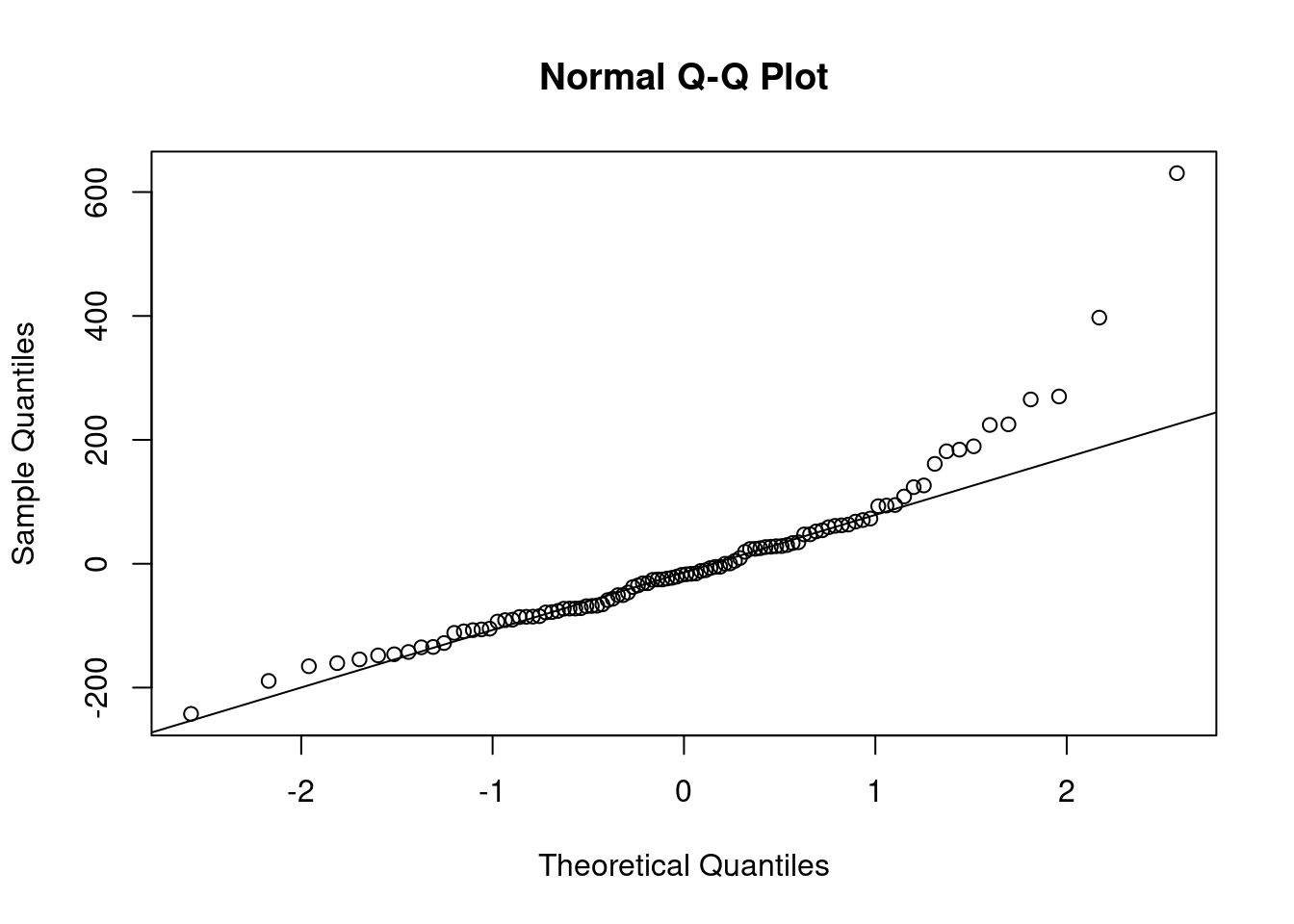

tibble(res = m3$residuals) %>% 
  ggplot(aes(res))+
  geom_histogram(aes(y = ..density..))+
  stat_function(fun = dnorm, args = list(mean = 0, sd = sd(m3$residuals)), color = "red")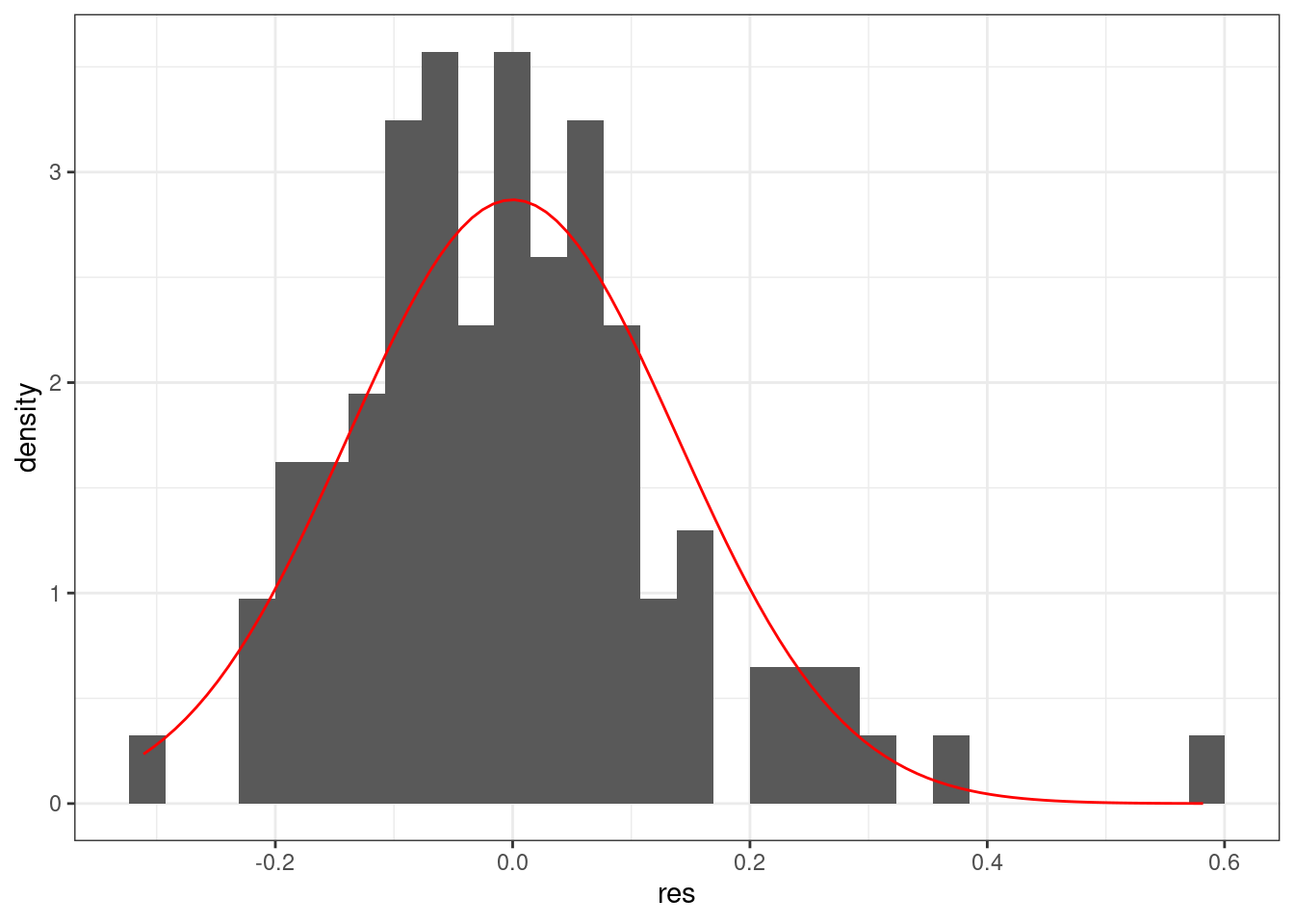

qqnorm(m3$residuals)
qqline(m3$residuals)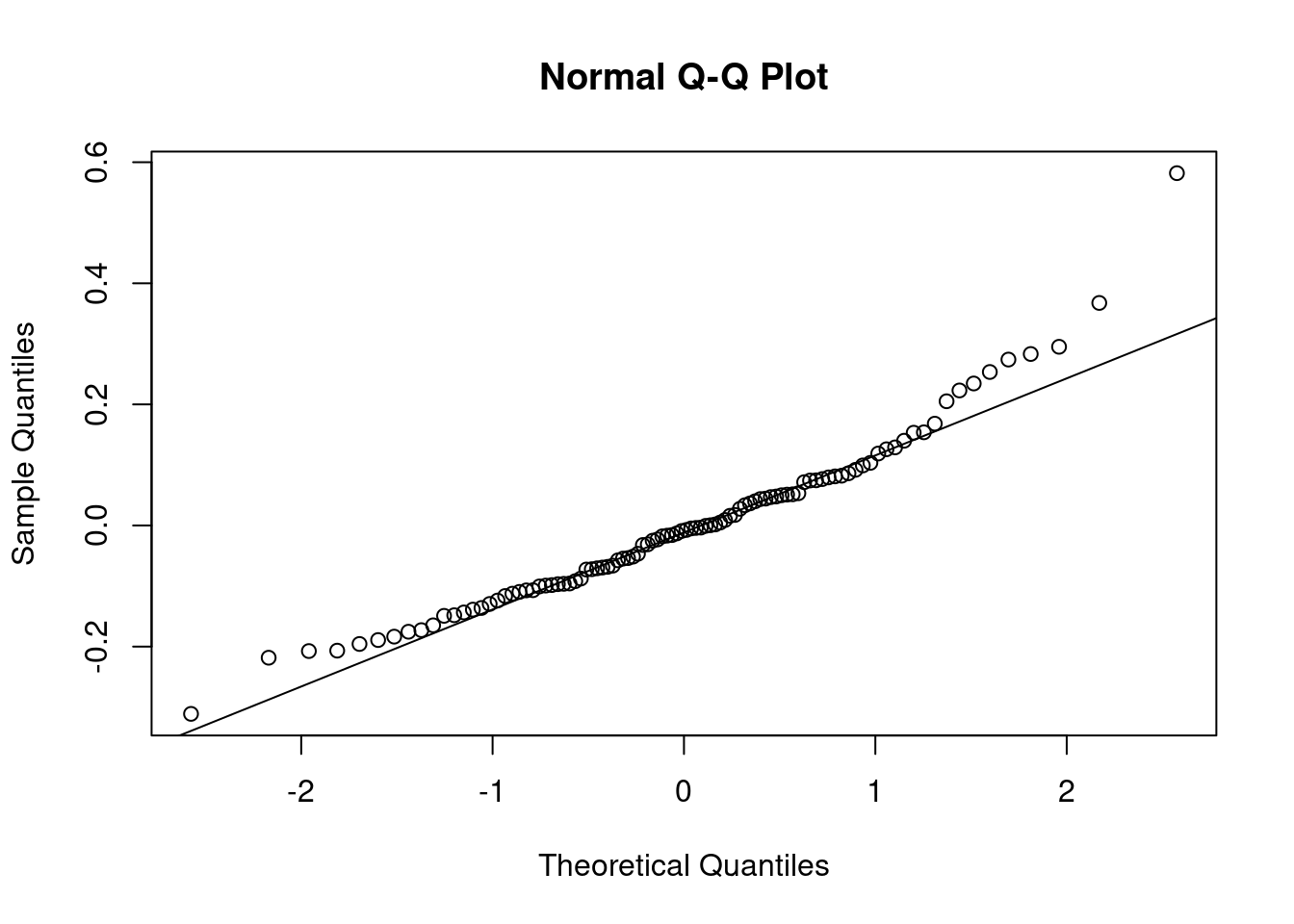

10.7 Гетероскидастичность

Распределение остатков непостоянно (т.е. не гомоскидастичны):

ldt %>% 
  ggplot(aes(Mean_RT, Freq))+
  geom_point()+
  theme_bw()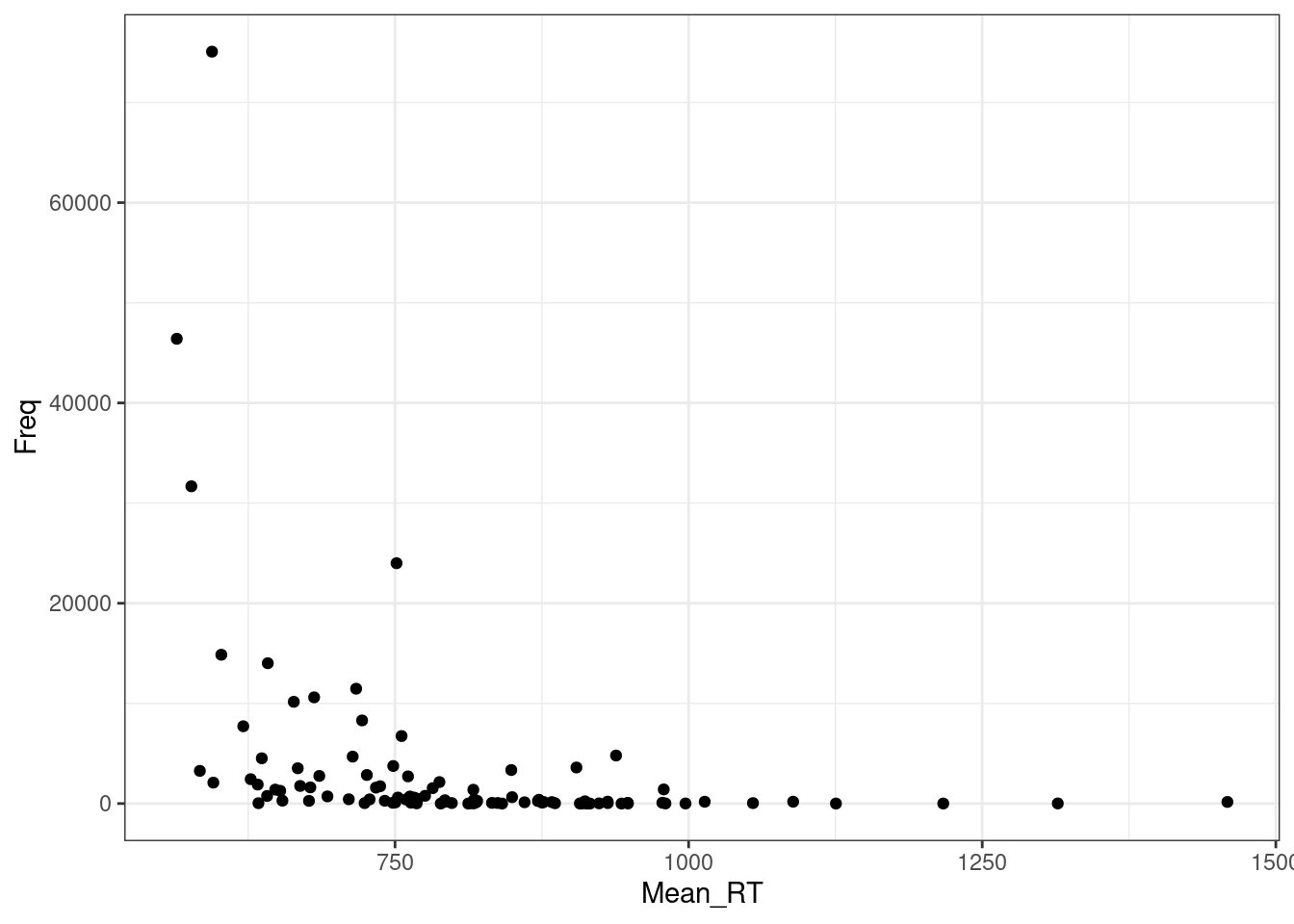

Тоже решается преобазованием данных.

10.8 Мультиколлинеарность

Линейная связь между некоторыми предикторами в модели.

• корреляционная матрица
• VIF (Variance inflation factor), car::vif()
  • VIF = 1 (Not correlated)
  • 1 < VIF < 5 (Moderately correlated)
  • VIF >=5 (Highly correlated)

10.9 Независимость наблюдений

Наблюдения должны быть независимы. В ином случае нужно использовать модель со смешанными эффектами.

10.9.1 Линейная модель со смешанными эффектами

В качестве примера мы попробуем поиграть с законом Хердана-Хипса, описывающий взаимосвязь количества уникальных слов в тексте в зависимости от длины текста. В датасете собраны некоторые корпуса Universal Dependencies (Zeman et al. 2020) и некоторые числа, посчитанные на их основании:

ud <- read_csv("https://raw.githubusercontent.com/agricolamz/2021_da4l/master/data/ud_corpora.csv")

ud %>% 
  ggplot(aes(n_words, n_tokens))+
  geom_point()+
  facet_wrap(~corpus, scale = "free")+
  geom_smooth(method = "lm", se = FALSE)+
  labs(x = "количество слов", 
       y = "количество уникальных слов",
       caption = "данные корпусов Universal Dependencies")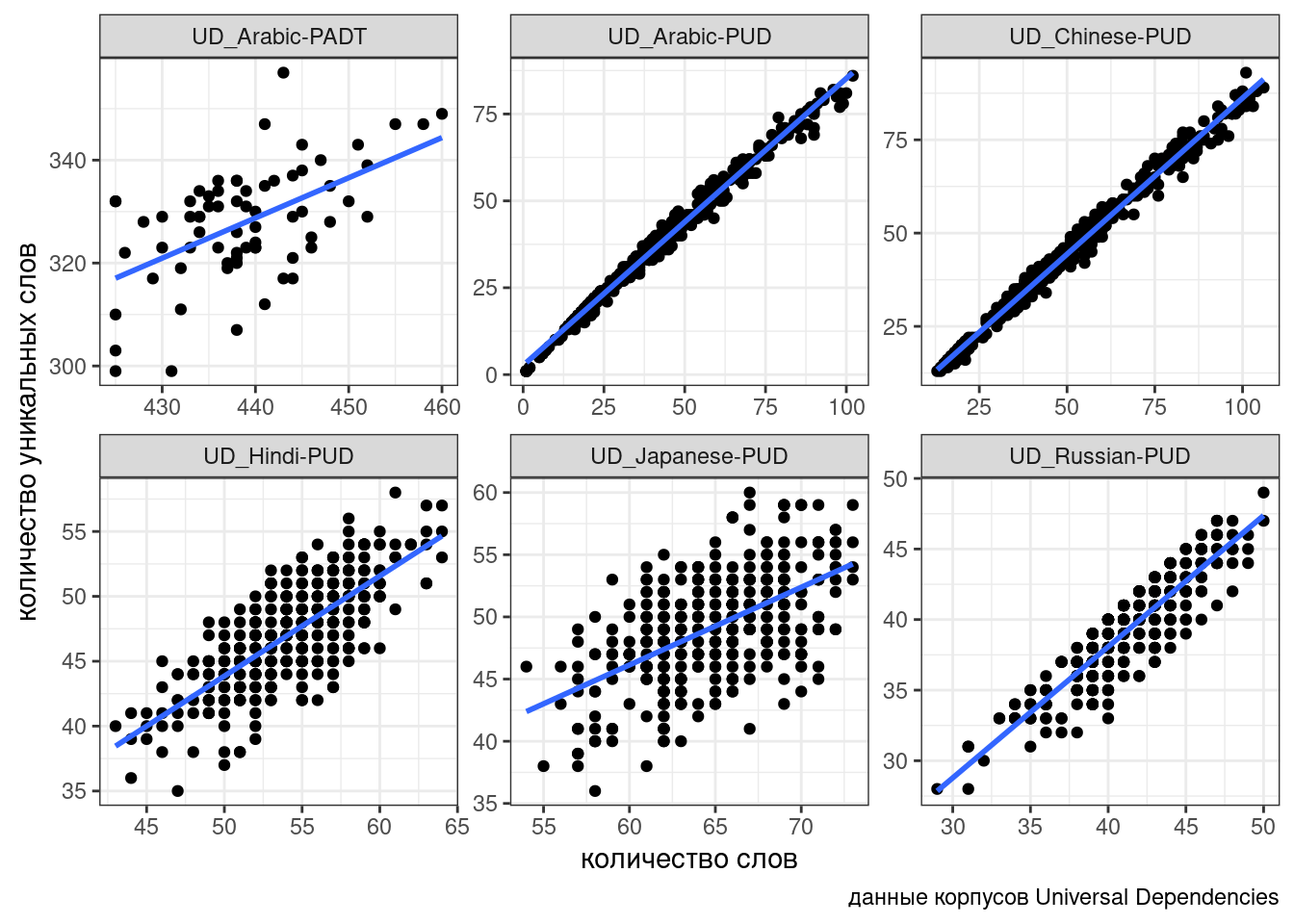

Связь между переменными безусловно линейная, однако в разных корпусах представлена разная перспектива: для каких-то корпусов, видимо, тексты специально нарезались, так что тексты таких корпусов содержат от 30-40 до 50-80 слов, а какие-то оставались не тронутыми. Чтобы показать, что связь есть, нельзя просто “слить” все наблюдения в один котел (см. парадокс Симпсона), так как это нарушит предположение регрессии о независимости наблюдений. Мы не можем включить переменную corpus в качестве dummy-переменной: тогда один из корпусов попадет в интерсепт (станет своего рода базовым уровенем), а остальные будут от него отсчитываться. К тому же не очень понятно, как работать с новыми данными из других корпусов: ведь мы хотим предсказывать значения обобщенно, вне зависимости от корпуса.

При моделировании при помощи моделей со случайными эффектами различают:

• основные эффекты – это те связи, которые нас интересуют, независимые переменные (количество слов, количество уникальных слов);
• случайные эффекты – это те переменные, которые создают группировку в данных (корпус).

В результате моделирования появляется обобщенная модель, которая игнорирует группировку, а потом для каждого значения случайного эффекта генерируется своя регрессия, отсчитывая от обобщенной модели как от базового уровня.

Рассмотрим простейший случай:

library(lme4)
library(lmerTest)

fit1 <- lmer(n_tokens~n_words+(1|corpus), data = ud)
summary(fit1)

Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: n_tokens ~ n_words + (1 | corpus)
   Data: ud

REML criterion at convergence: 10321.5

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-7.5271 -0.4947  0.0354  0.5282  8.6350 

Random effects:
 Groups   Name        Variance Std.Dev.
 corpus   (Intercept) 240.608  15.512  
 Residual               8.844   2.974  
Number of obs: 2046, groups:  corpus, 6

Fixed effects:
               Estimate  Std. Error          df t value            Pr(>|t|)    
(Intercept)   -4.527634    6.353147    4.958748  -0.713               0.508    
n_words        0.827933    0.004418 1992.686553 187.415 <0.0000000000000002 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
        (Intr)
n_words -0.079

ud %>% 
  mutate(predicted = predict(fit1)) %>% 
  ggplot(aes(n_words, n_tokens))+
  geom_point()+
  facet_wrap(~corpus, scale = "free")+
  geom_line(aes(y = predicted), color = "red") +
  labs(x = "количество слов", 
       y = "количество уникальных слов",
       caption = "данные корпусов Universal Dependencies")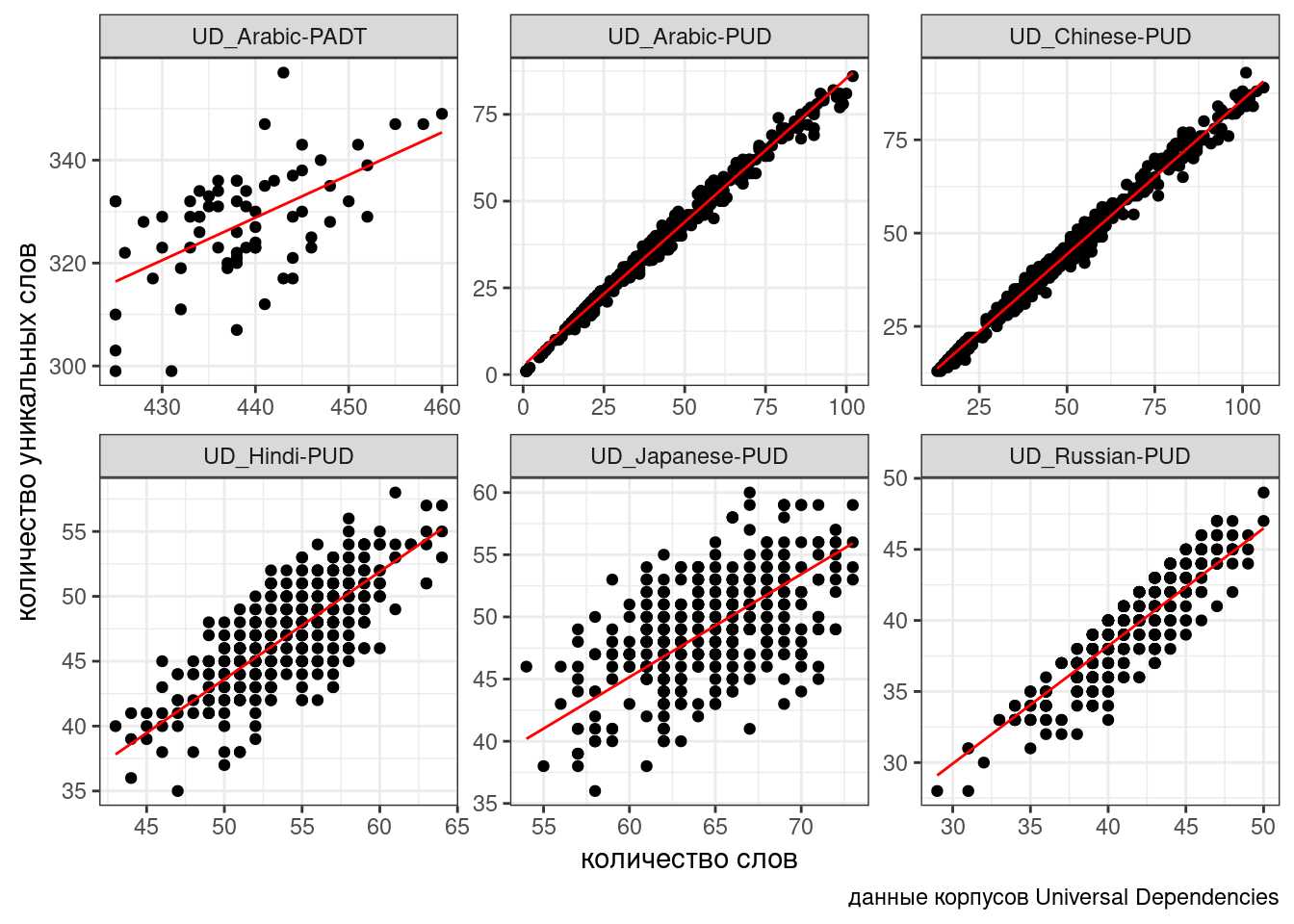

Можно посмотреть на предсказания модели (основные эффекты):

library(ggeffects)
ggeffect(fit1) %>% 
  plot()

$n_words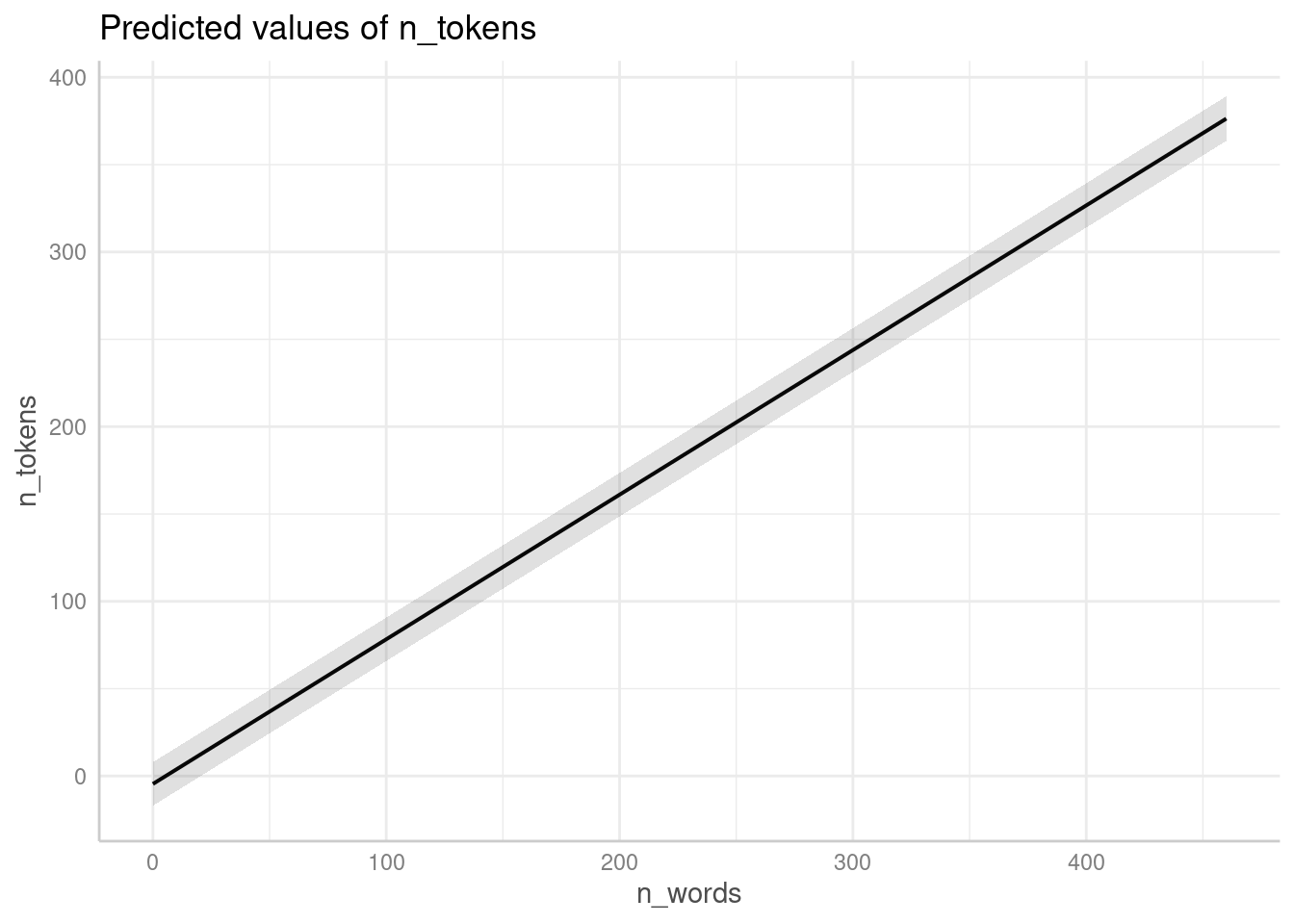

Визуализируйте полученные модели при помощи функции plot(). Какие ограничения на применение линейной регрессии нарушается в наших моделях?

plot(fit1)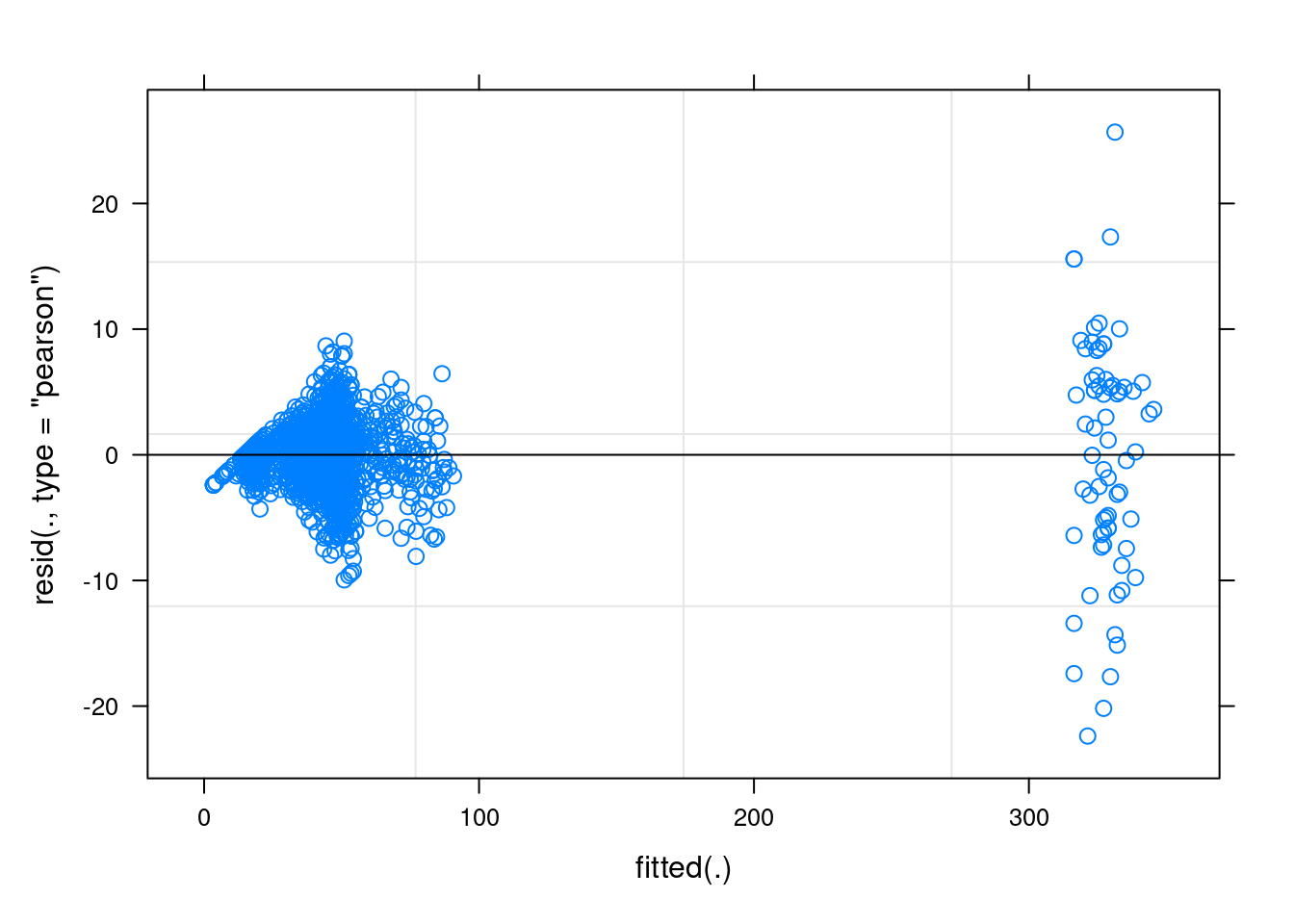

В данном случае мы предполагаем, что случайный эффект имеет случайный свободный член. Т.е. все получающиеся линии параллельны, так как имеют общий угловой коэффициент. Можно допустить большую свободу и сделать так, чтобы в случайном эффекте были не только интерсепт, но и свободный член:

fit2 <- lmer(n_tokens~n_words+(1+n_words|corpus), data = ud)
summary(fit2)

Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: n_tokens ~ n_words + (1 + n_words | corpus)
   Data: ud

REML criterion at convergence: 10275.2

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-7.8337 -0.5003  0.0293  0.5172  8.8405 

Random effects:
 Groups   Name        Variance Std.Dev. Corr 
 corpus   (Intercept) 4.465751 2.11323       
          n_words     0.009532 0.09763  -1.00
 Residual             8.693060 2.94840       
Number of obs: 2046, groups:  corpus, 6

Fixed effects:
            Estimate Std. Error      df t value  Pr(>|t|)    
(Intercept)  3.23103    0.88937 2.21775   3.633    0.0582 .  
n_words      0.80323    0.04005 4.10414  20.056 0.0000299 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
        (Intr)
n_words -0.988
optimizer (nloptwrap) convergence code: 0 (OK)
boundary (singular) fit: see help('isSingular')

ud %>% 
  mutate(predicted = predict(fit2)) %>% 
  ggplot(aes(n_words, n_tokens))+
  geom_point()+
  facet_wrap(~corpus, scale = "free")+
  geom_line(aes(y = predicted), color = "red") +
  labs(x = "количество слов", 
       y = "количество уникальных слов",
       caption = "данные корпусов Universal Dependencies")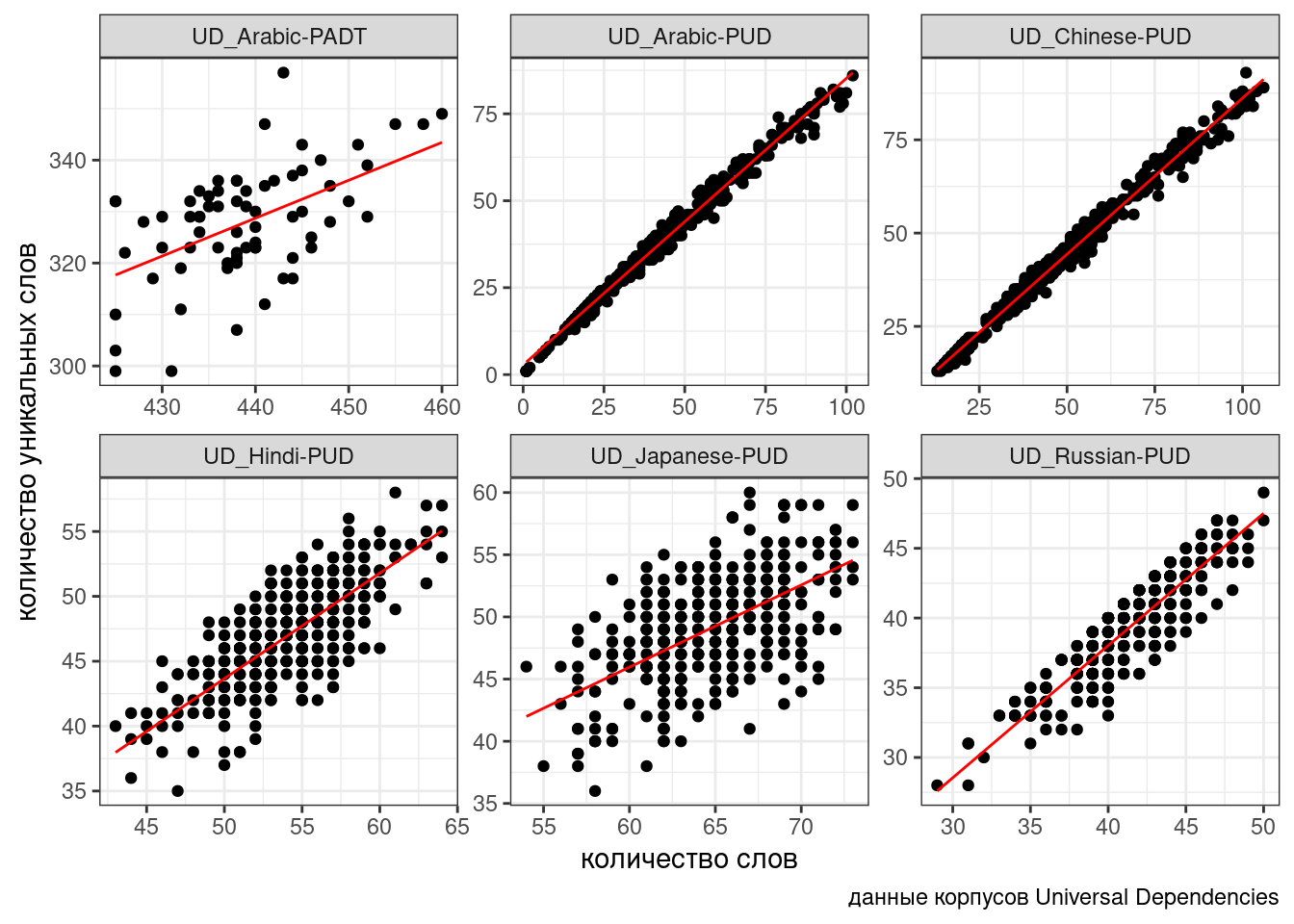

Можно посмотреть на предсказания модели (основные эффекты):

ggeffect(fit2) %>% 
  plot()

$n_words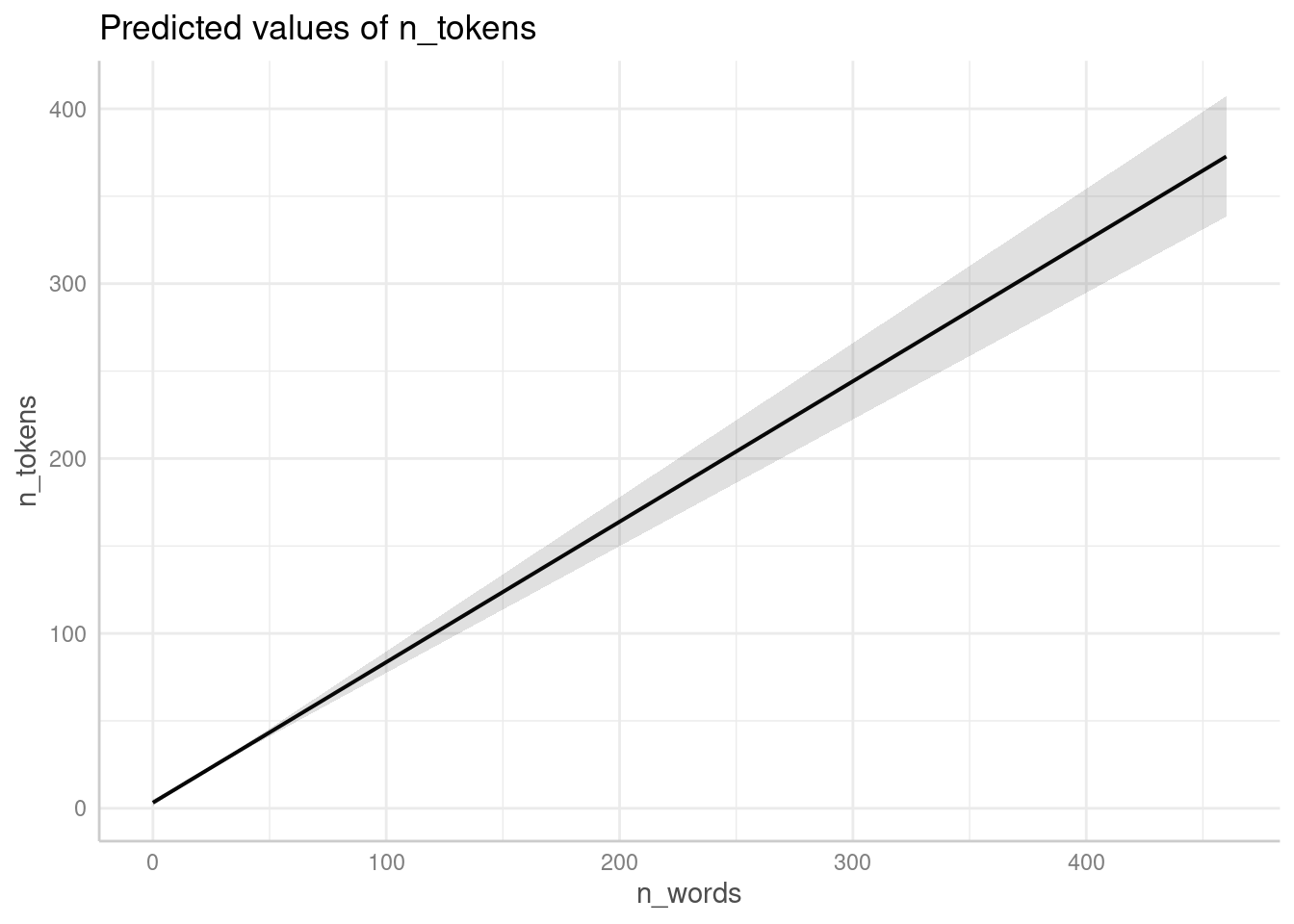

Нарушения все те же:

plot(fit2)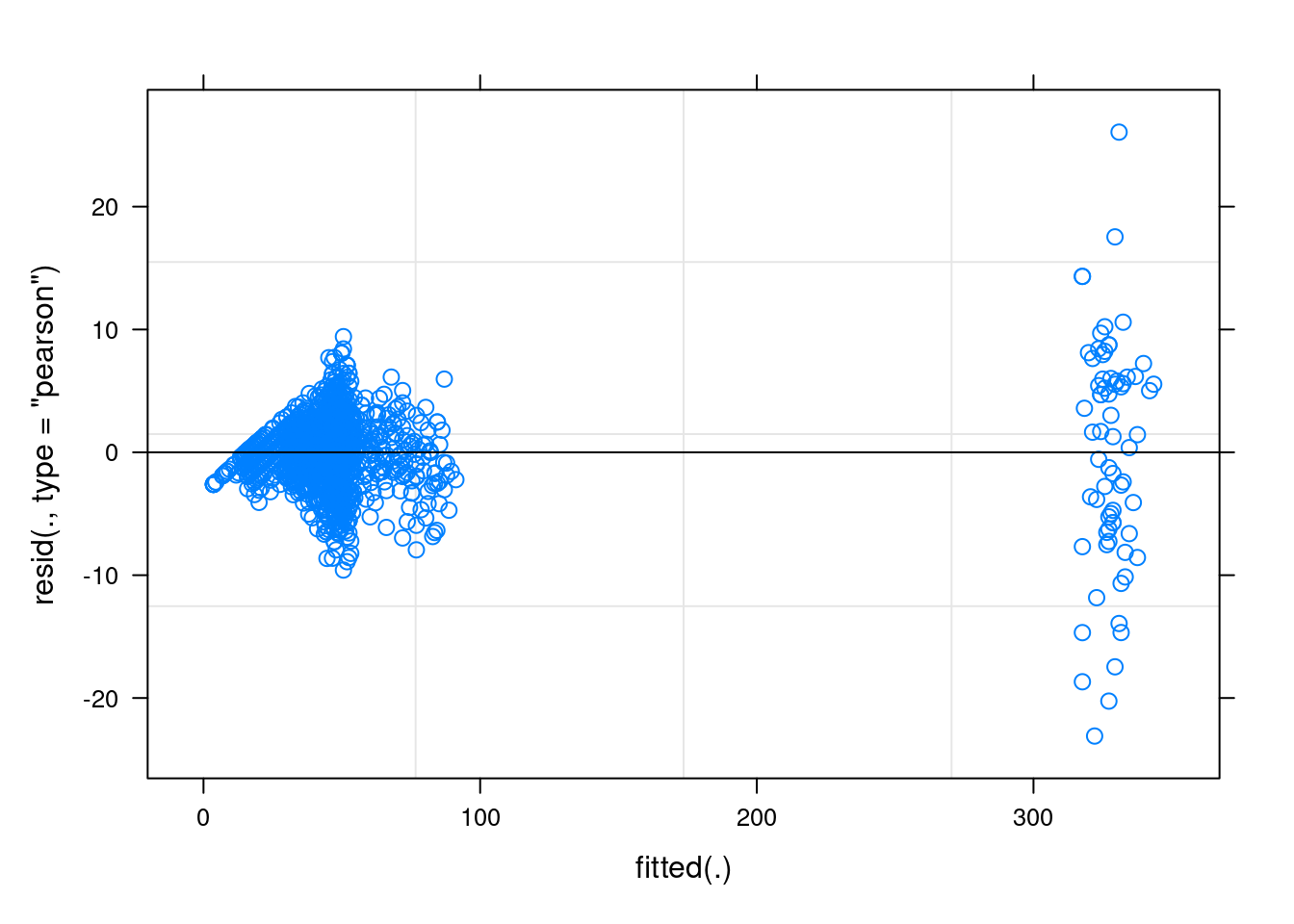

При желании мы можем также построить модель, в которой в случайном эффекте будет лишь угловой коэффициент, а свободный член будет фиксированным:

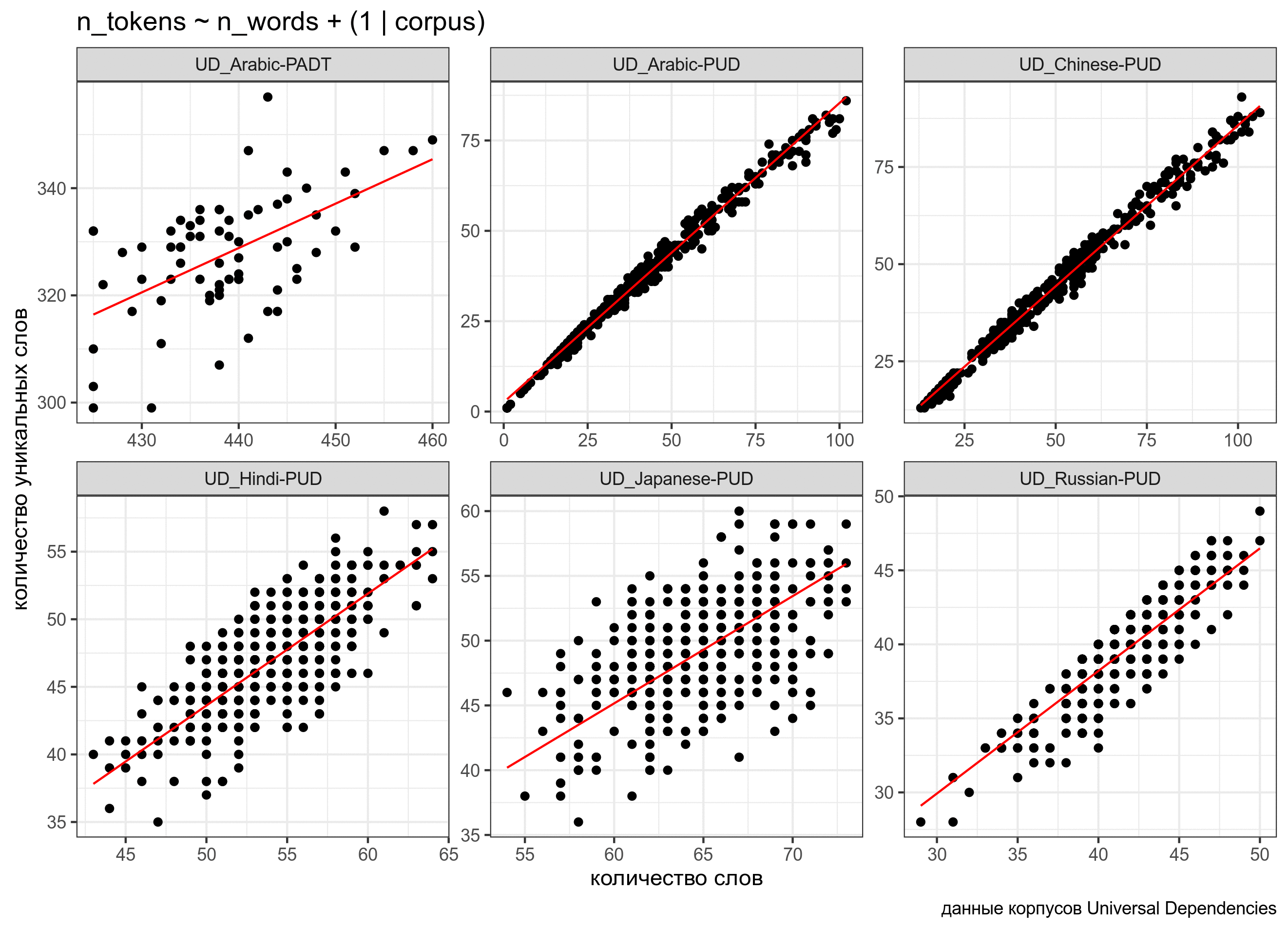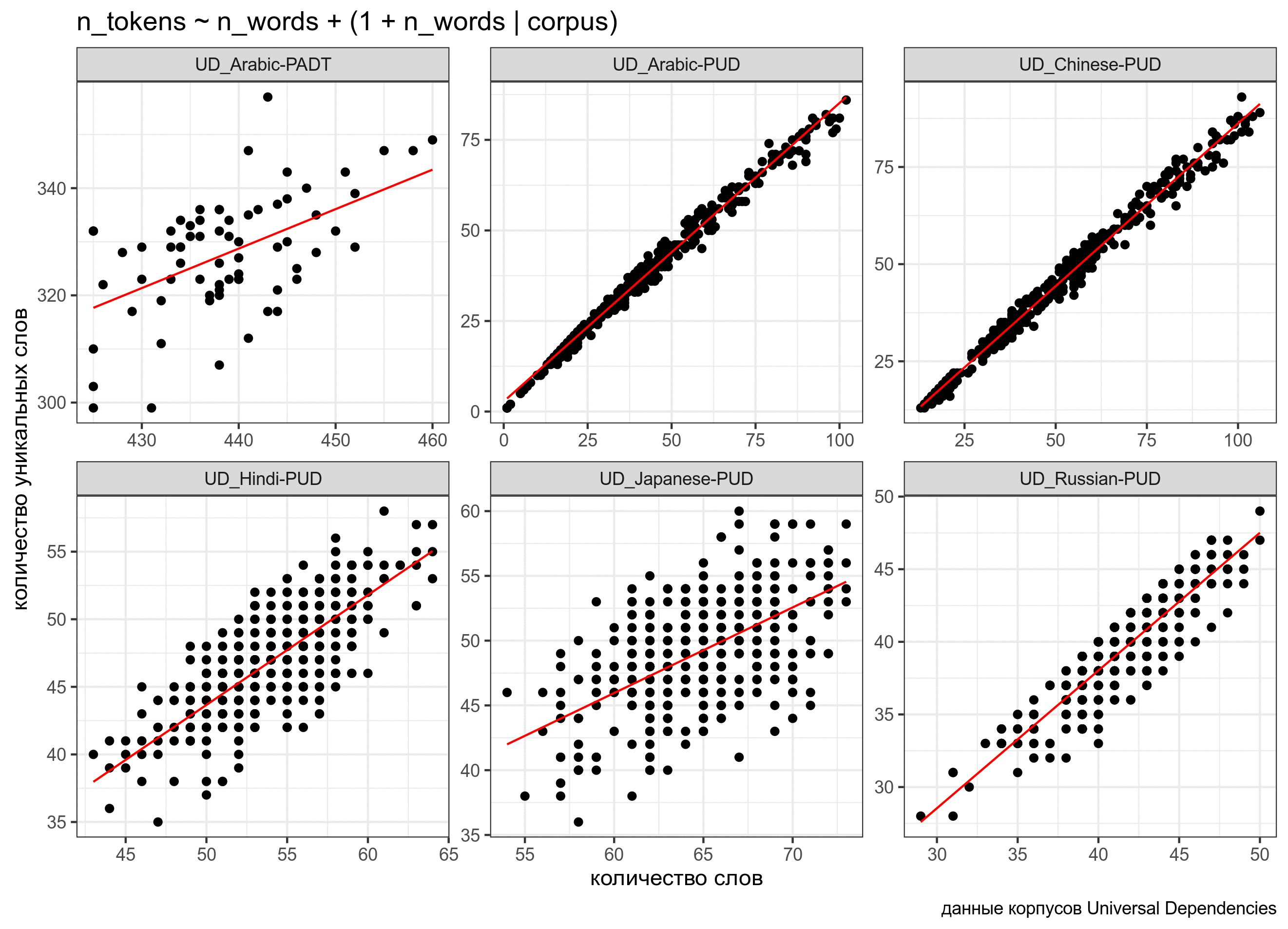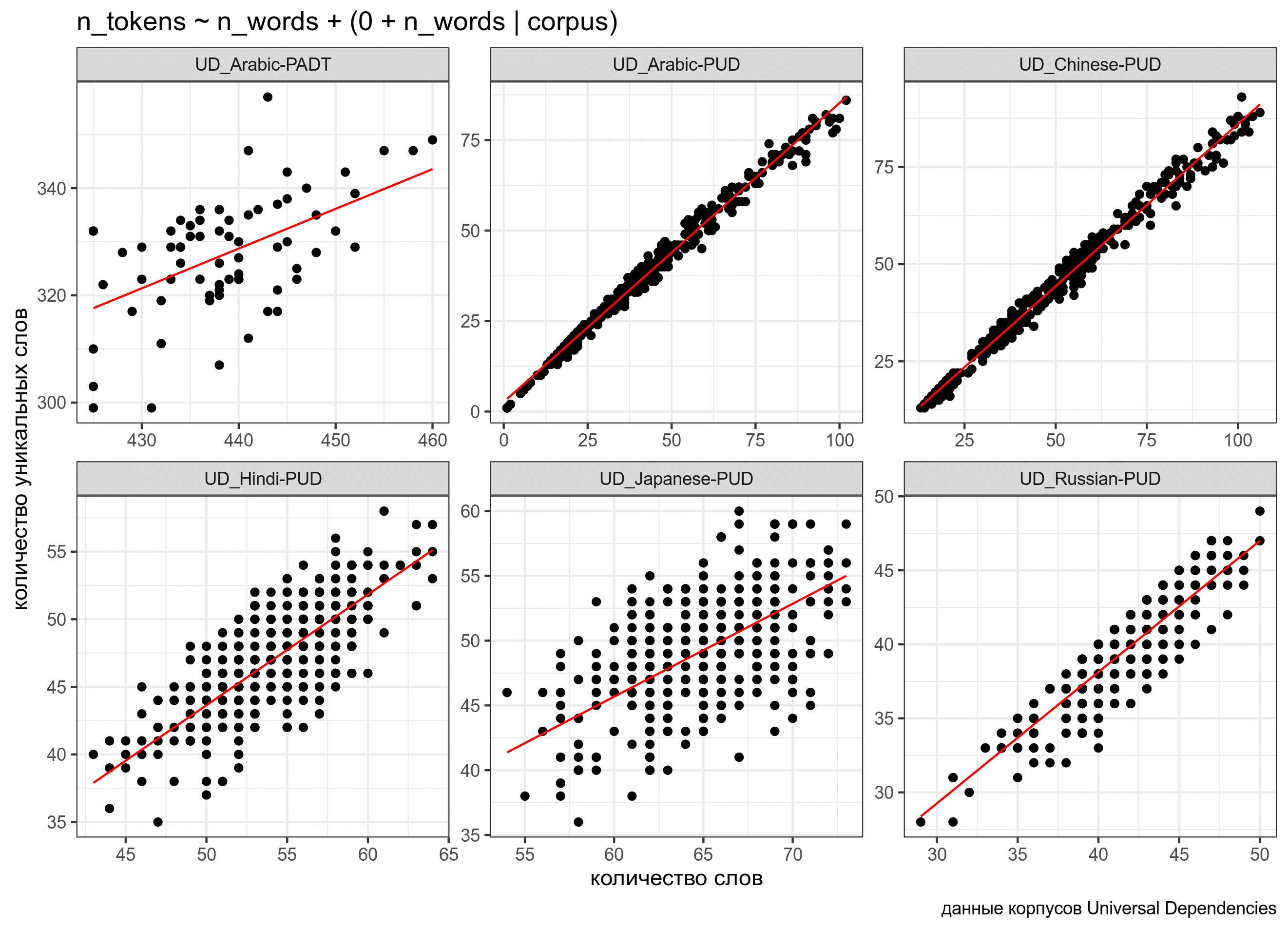
fit3 <- lmer(n_tokens~n_words+(0+n_words|corpus), data = ud)
summary(fit3)

Linear mixed model fit by REML. t-tests use Satterthwaite's method [
lmerModLmerTest]
Formula: n_tokens ~ n_words + (0 + n_words | corpus)
   Data: ud

REML criterion at convergence: 10280.9

Scaled residuals: 
    Min      1Q  Median      3Q     Max 
-7.8107 -0.4933  0.0315  0.5227  8.8209 

Random effects:
 Groups   Name    Variance Std.Dev.
 corpus   n_words 0.004023 0.06343 
 Residual         8.717996 2.95263 
Number of obs: 2046, groups:  corpus, 6

Fixed effects:
              Estimate Std. Error         df t value             Pr(>|t|)    
(Intercept)    2.64805    0.21627 2043.59791   12.24 < 0.0000000000000002 ***
n_words        0.80427    0.02615    5.16230   30.76          0.000000477 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Correlation of Fixed Effects:
        (Intr)
n_words -0.132

ud %>% 
  mutate(predicted = predict(fit3)) %>% 
  ggplot(aes(n_words, n_tokens))+
  geom_point()+
  facet_wrap(~corpus, scale = "free")+
  geom_line(aes(y = predicted), color = "red") +
  labs(x = "количество слов", 
       y = "количество уникальных слов",
       caption = "данные корпусов Universal Dependencies")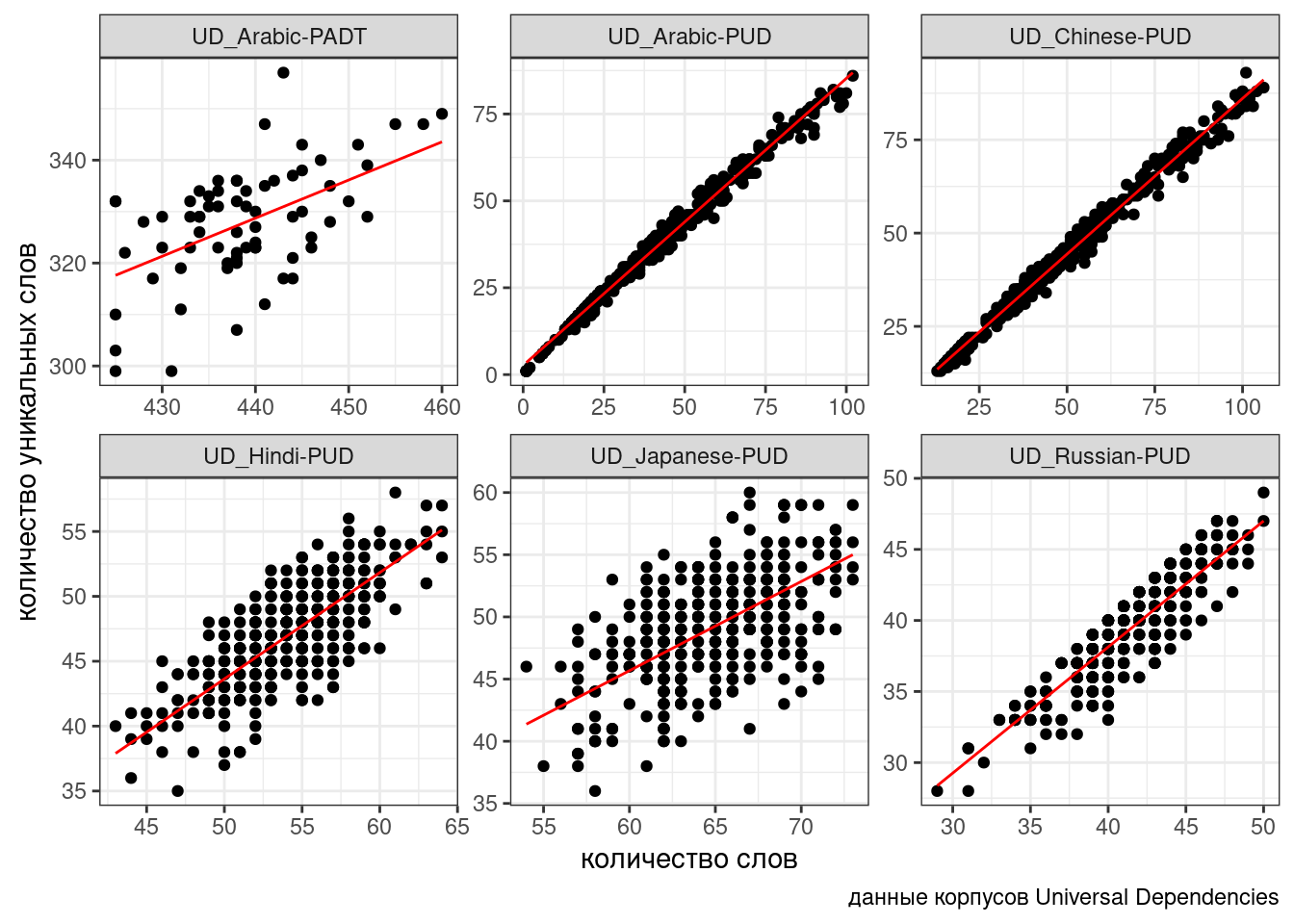

Линии получились очень похожими, но разными:

Можно посмотреть на предсказания модели (основные эффекты):

ggeffect(fit3) %>% 
  plot()

$n_words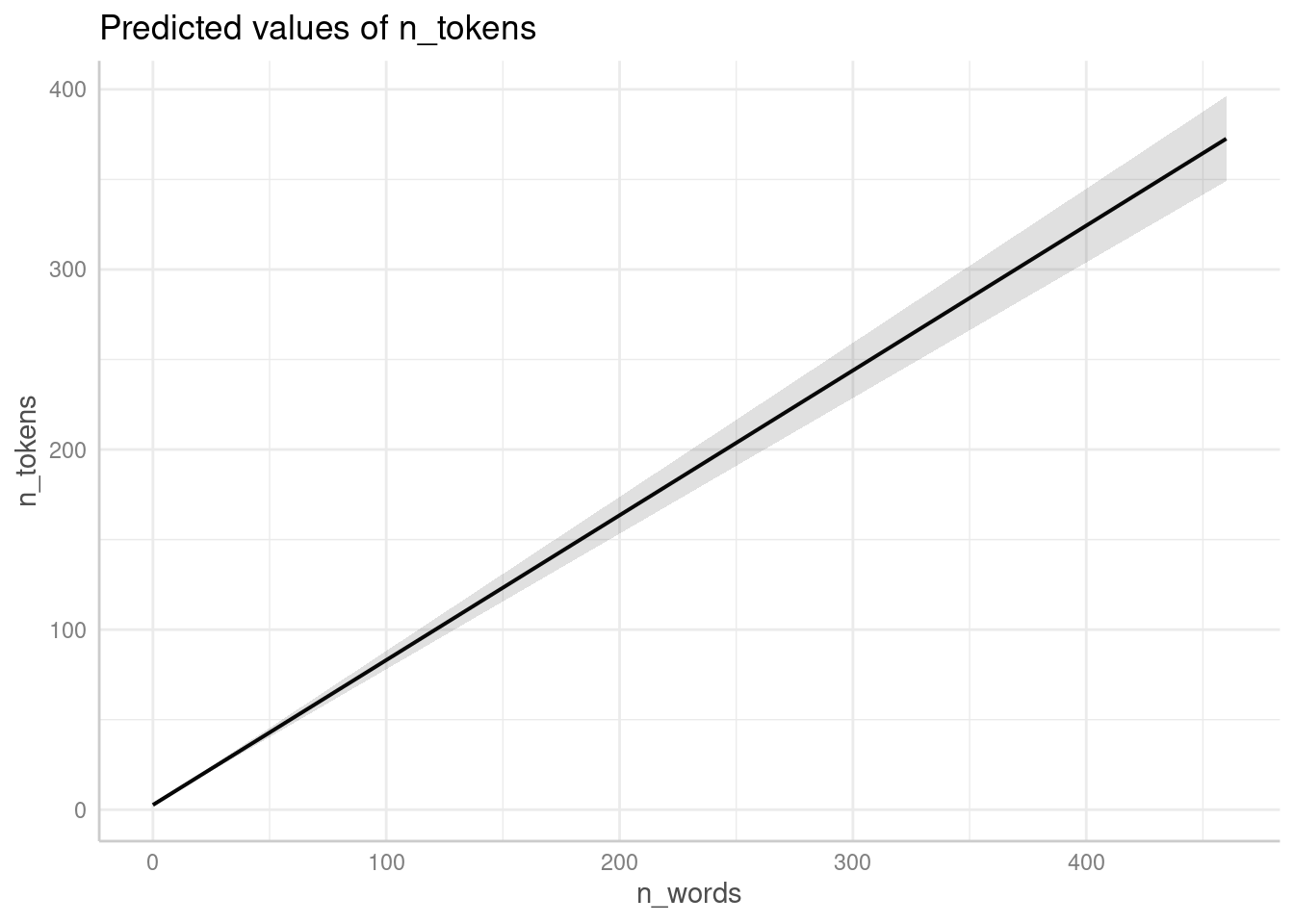

Нарушения все те же:

plot(fit3)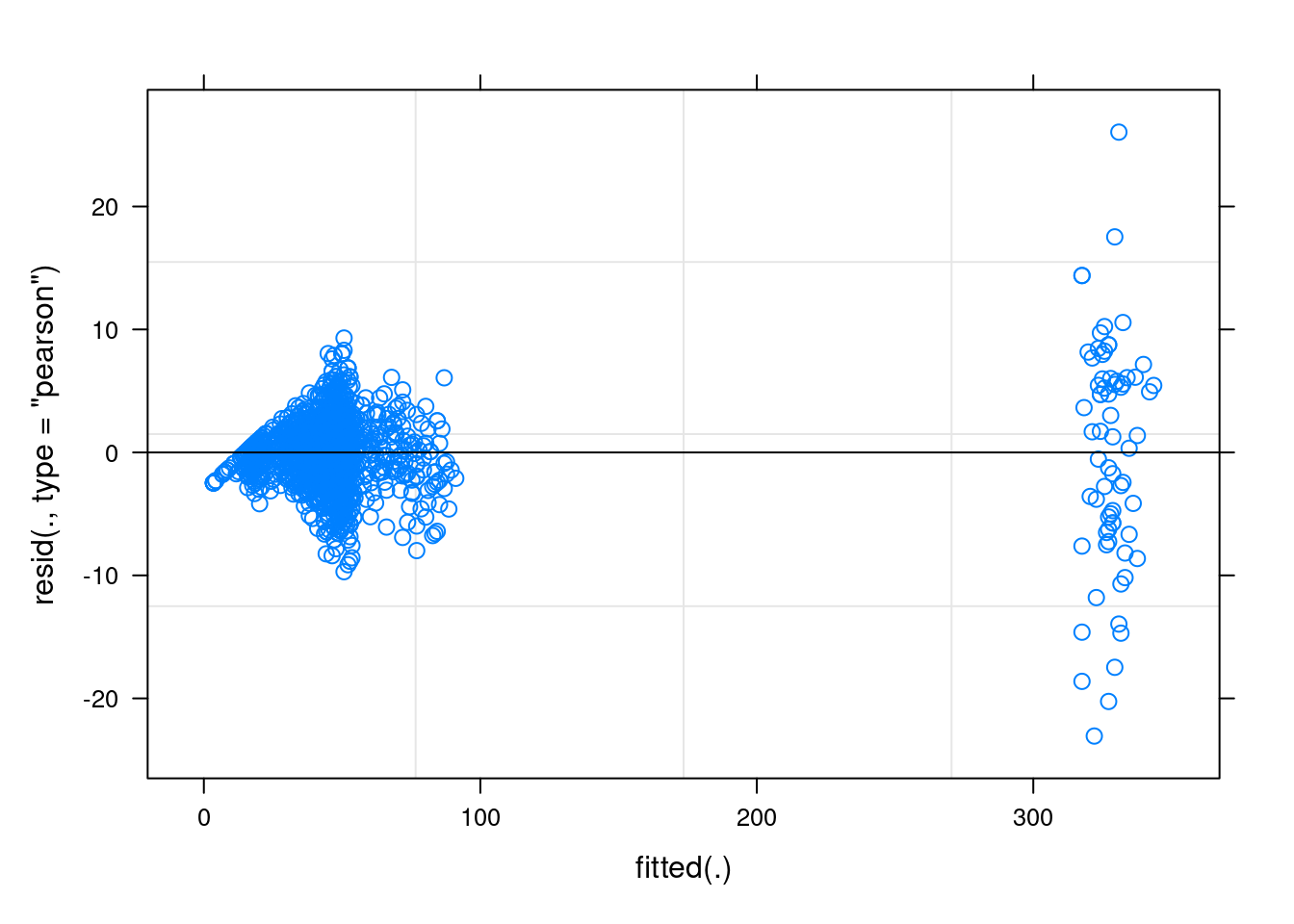

Сравним полученные модели:

anova(fit3, fit2, fit1)

Постройте модель со случайными угловым коэффициентом и свободным членом, устранив проблему, которую вы заметили в прошлом задании.

Пользуясь знаниями из предыдущих заданий, смоделируйте связь количества слов и количества существительных. С какими проблемами вы столкнулись?

Ссылки на литературу

Zeman, D., J. Nivre, Mitchell Abrams, Elia Ackermann, Noëmi Aepli, Hamid Aghaei, Željko Agić, et al. 2020. “Universal Dependencies 2.7.” http://hdl.handle.net/11234/1-3424.

Ляшевская, О. Н., and С. А. Шаров. 2009. Частотный Словарь Современного Русского Языка: На Материалах Национального Корпуса Русского Языка. Азбуковник.

---

2. Как и в других функциях, вычисляющих описательную статистику (mean(), median(), max(), min() и др.), функция var() (и все остальные функции, которые мы будем обсуждать sd(), cov()) возвращают NA, если в векторе есть пропущенные значения. Чтобы изменить это поведение, нужно добавить аргумент na.rm = TRUE.↩︎