8 Эмпирическая байесовская оценка

library(tidyverse)

Метод эмпирической байесовской оценки (Empirical Bayes estimation) — один из байесовских методов, в рамках которого:

производят оценку априорного распределения вероятностей на основании имеющихся данных
используют полученное априорное распределение для получение апостериорной оценки для каждого наблюдения

Рассмотрим пример данных из статьи (Daniel et al. 2019), в которой аннализировались интервью с людьми из деревени Михалёвская и исследовался ряд консервативных и инновативных черт в их речи.

mikhalevskaja <- read_csv("https://raw.githubusercontent.com/agricolamz/2022_da4l/master/data/ustya_data.csv")
glimpse(mikhalevskaja)

Rows: 359
Columns: 7
$ speaker      <chr> "avm1922", "ans1925", "avt1928", "egp1928", "lpp1928", "p…
$ year         <dbl> 1922, 1925, 1928, 1928, 1928, 1928, 1930, 1933, 1935, 194…
$ gender       <chr> "f", "f", "f", "f", "f", "f", "m", "f", "f", "f", "f", "f…
$ conservative <dbl> 92, 56, 12, 33, 2, 83, 22, 22, 33, 60, 58, 11, 55, 8, 30,…
$ innovative   <dbl> 60, 70, 46, 127, 23, 127, 41, 88, 85, 103, 200, 73, 70, 5…
$ total        <dbl> 152, 126, 58, 160, 25, 210, 63, 110, 118, 163, 258, 84, 1…
$ feature      <chr> "adj", "adj", "adj", "adj", "adj", "adj", "adj", "adj", "…

Представим себе, что мы решили задаться целью найти наиболее диалектных носителей:

library(tidytext)
mikhalevskaja %>% 
  mutate(ratio = conservative/total,
         speaker = reorder_within(speaker, ratio, feature)) %>% 
  ggplot(aes(ratio, speaker, color = gender))+
  geom_point()+
  facet_wrap(~feature, scales = "free")+
  scale_y_reordered()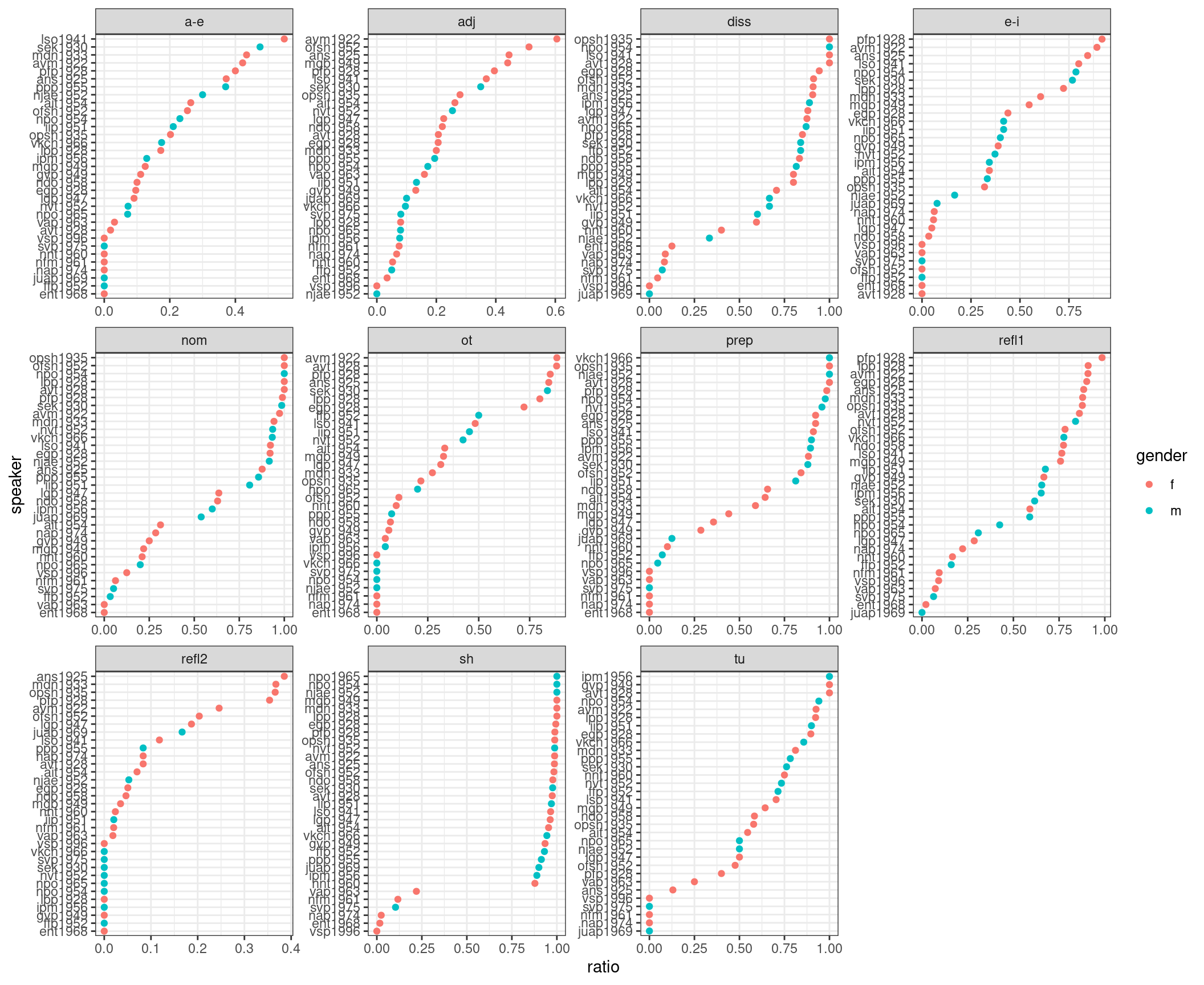

Не очень легко это анализировать… Давайте выберем один признак – подъем a: консервативными считались формы [ꞌpʲetʲero], а инновативной – реализация [ꞌpʲatʲərə]. Посчитаем долю и отсортируем:

mikhalevskaja %>% 
  filter(feature == "a-e") %>% 
  mutate(ratio = conservative/total) %>% 
  arrange(desc(ratio))

ABCDEFGHIJ0123456789

speaker <chr>	year <dbl>	gender <chr>	conservative <dbl>	innovative <dbl>	total <dbl>	feature <chr>	ratio <dbl>
lso1941	1941	f	134	110	244	a-e	0.54918033
sek1930	1930	m	48	53	101	a-e	0.47524752
mdn1933	1933	f	33	43	76	a-e	0.43421053
avm1922	1922	f	57	78	135	a-e	0.42222222
pfp1928	1928	f	66	99	165	a-e	0.40000000
ans1925	1925	f	80	135	215	a-e	0.37209302
ppp1955	1955	m	10	17	27	a-e	0.37037037
njae1952	1952	m	3	7	10	a-e	0.30000000
ait1954	1954	f	19	53	72	a-e	0.26388889
ofsh1952	1952	f	17	50	67	a-e	0.25373134

В целом, всего в интервью встречается от 4 до 244 контекстов для реализации признака. Хотим ли мы верить, что lpp1928 с 29 наблюдениями диалектнее, чем mgb1949 с 104 наблюдениями, только на основании доли?

mikhalevskaja %>% 
  filter(feature  == "a-e") %>% 
  mutate(ratio = conservative/total) %>% 
  ggplot(aes(ratio))+
  geom_histogram()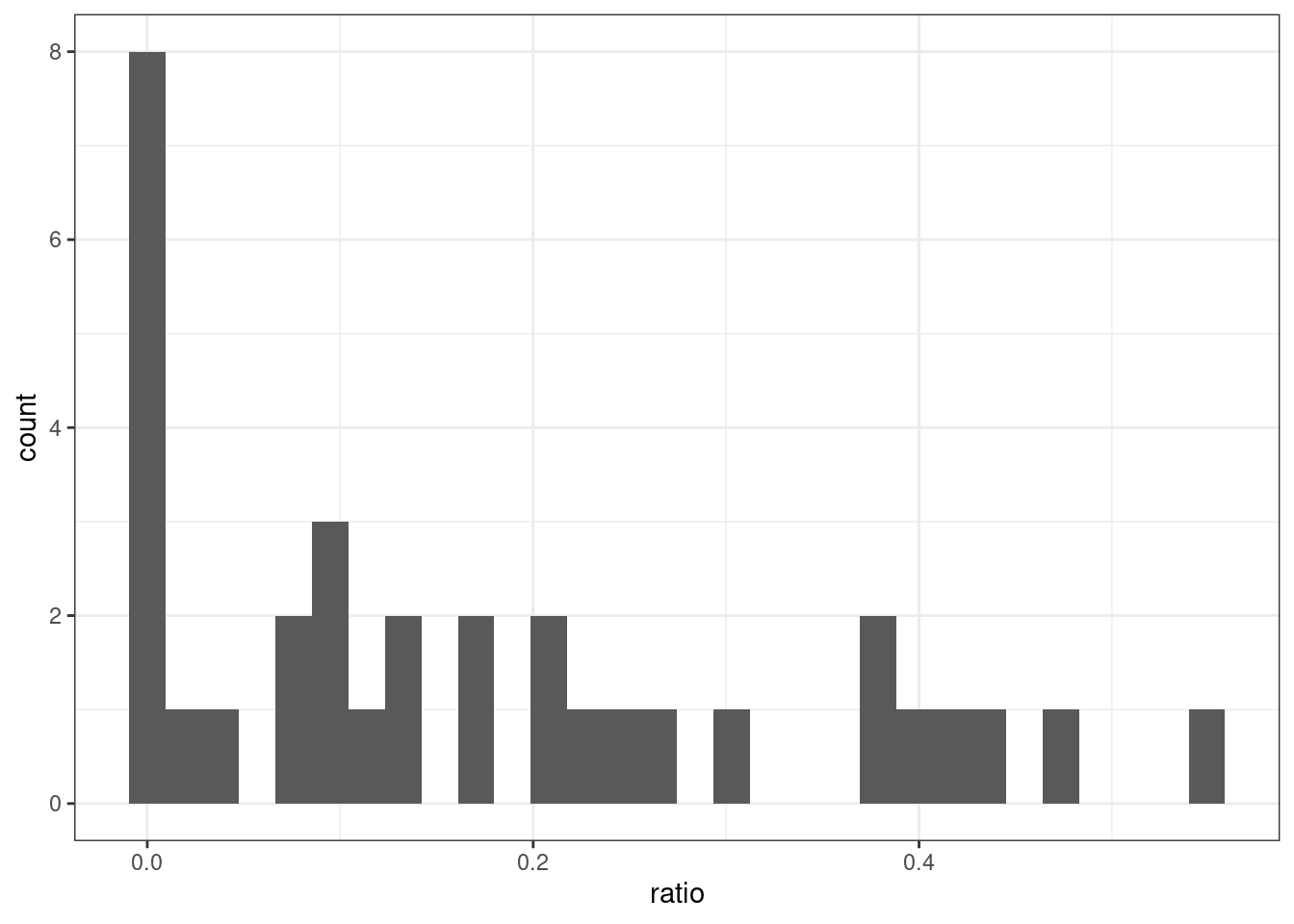

Мы можем провести байесовский апдейт, но для этого нам нужно априорное распределение. Трюк, который предлагает байесовская эмпирическая оценка заключается в том, что априорное распределение можно попробовать получить на основании данных:

mikhalevskaja %>% 
  filter(feature == "a-e") %>% 
  mutate(ratio = conservative/total) %>% 
  filter(ratio != 0, # оказывается fitdist плохо работает, когда много крайних точек
         ratio != 1) ->
  for_beta_estimation 
  
beta_est <- fitdistrplus::fitdist(for_beta_estimation$ratio, distr = 'beta', method = 'mle')
beta_est

Fitting of the distribution ' beta ' by maximum likelihood 
Parameters:
       estimate Std. Error
shape1 1.590621  0.4127354
shape2 5.445977  1.5766951

Сделаем байесовский апдейт:

mikhalevskaja %>% 
  filter(feature == "a-e") %>% 
  mutate(alpha_prior = beta_est$estimate[1],
         beta_prior = beta_est$estimate[2],
         alpha_post = conservative+alpha_prior,
         beta_post  = innovative+beta_prior,
         mean_post = alpha_post/(alpha_post+beta_post),
         ratio = conservative/total) %>% 
  ggplot(aes(ratio, mean_post, label = speaker, color = total))+
  geom_hline(yintercept = beta_est$estimate[1]/sum(beta_est$estimate), linetype = 2)+
  geom_point()+
  ggrepel::geom_text_repel()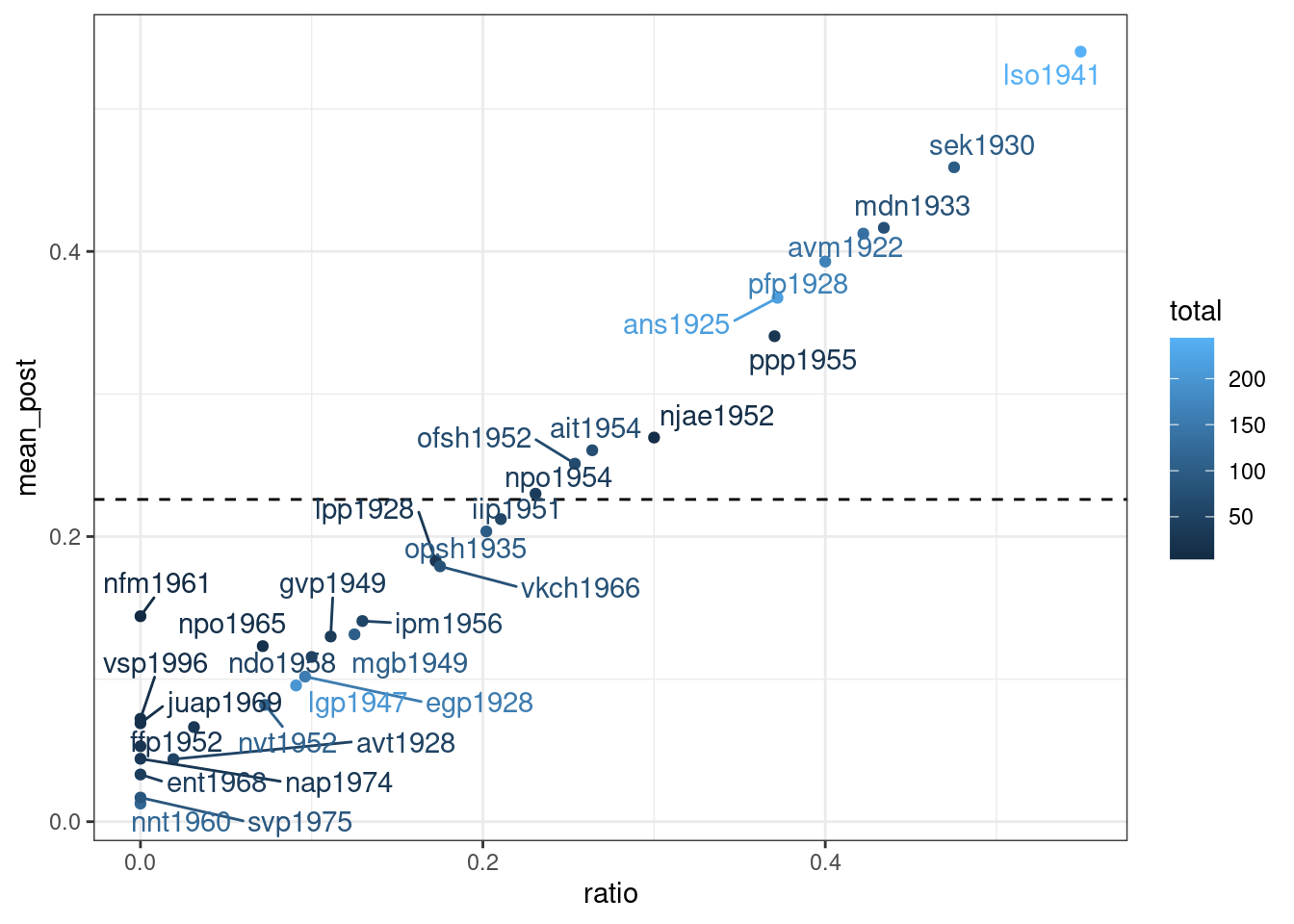

Как видно, байесовская оценка не сильно отличается от старой оценки средним, однако таким образом мы можем видеть, что после байесовского апдейта наблюдения с маленьким количеством наблюдений льнут к среднему априорного распределения. Мы можем даже умножить параметры нашего априорного распределения на 10, чтобы показать это:

mikhalevskaja %>% 
  filter(feature == "a-e") %>% 
  mutate(alpha_prior = beta_est$estimate[1]*10,
         beta_prior = beta_est$estimate[2]*10,
         alpha_post = conservative+alpha_prior,
         beta_post  = innovative+beta_prior,
         mean_post = alpha_post/(alpha_post+beta_post),
         ratio = conservative/total) %>% 
  ggplot(aes(ratio, mean_post, label = speaker, color = total))+
  geom_hline(yintercept = beta_est$estimate[1]/sum(beta_est$estimate), linetype = 2)+
  geom_point()+
  ggrepel::geom_text_repel()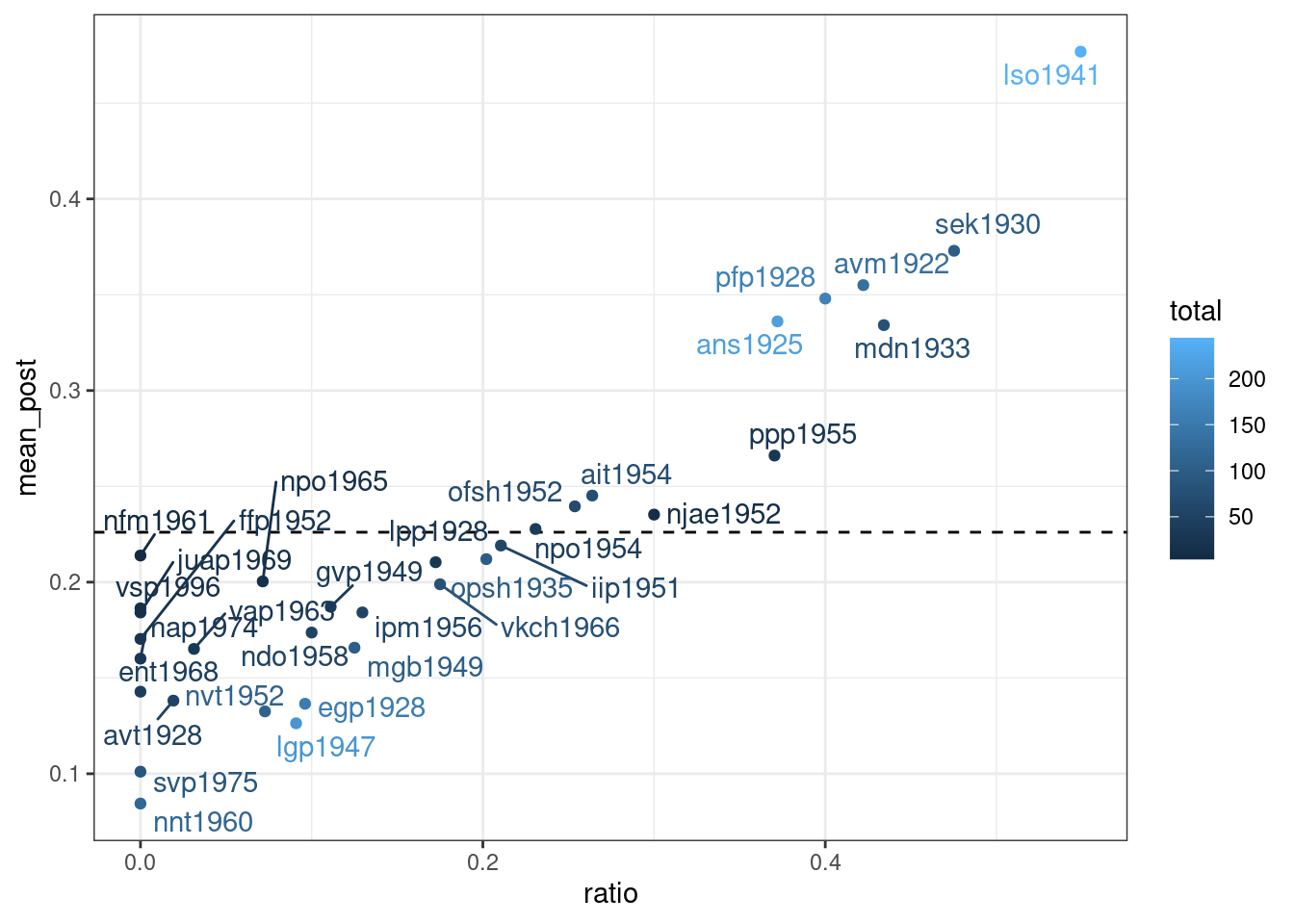

mikhalevskaja %>% 
  filter(feature == "a-e") %>% 
  mutate(alpha_prior = beta_est$estimate[1]*40,
         beta_prior = beta_est$estimate[2]*40,
         alpha_post = conservative+alpha_prior,
         beta_post  = innovative+beta_prior,
         mean_post = alpha_post/(alpha_post+beta_post),
         ratio = conservative/total) %>% 
  ggplot(aes(ratio, mean_post, label = speaker, color = total))+
  geom_hline(yintercept = beta_est$estimate[1]/sum(beta_est$estimate), linetype = 2)+
  geom_point()+
  ggrepel::geom_text_repel()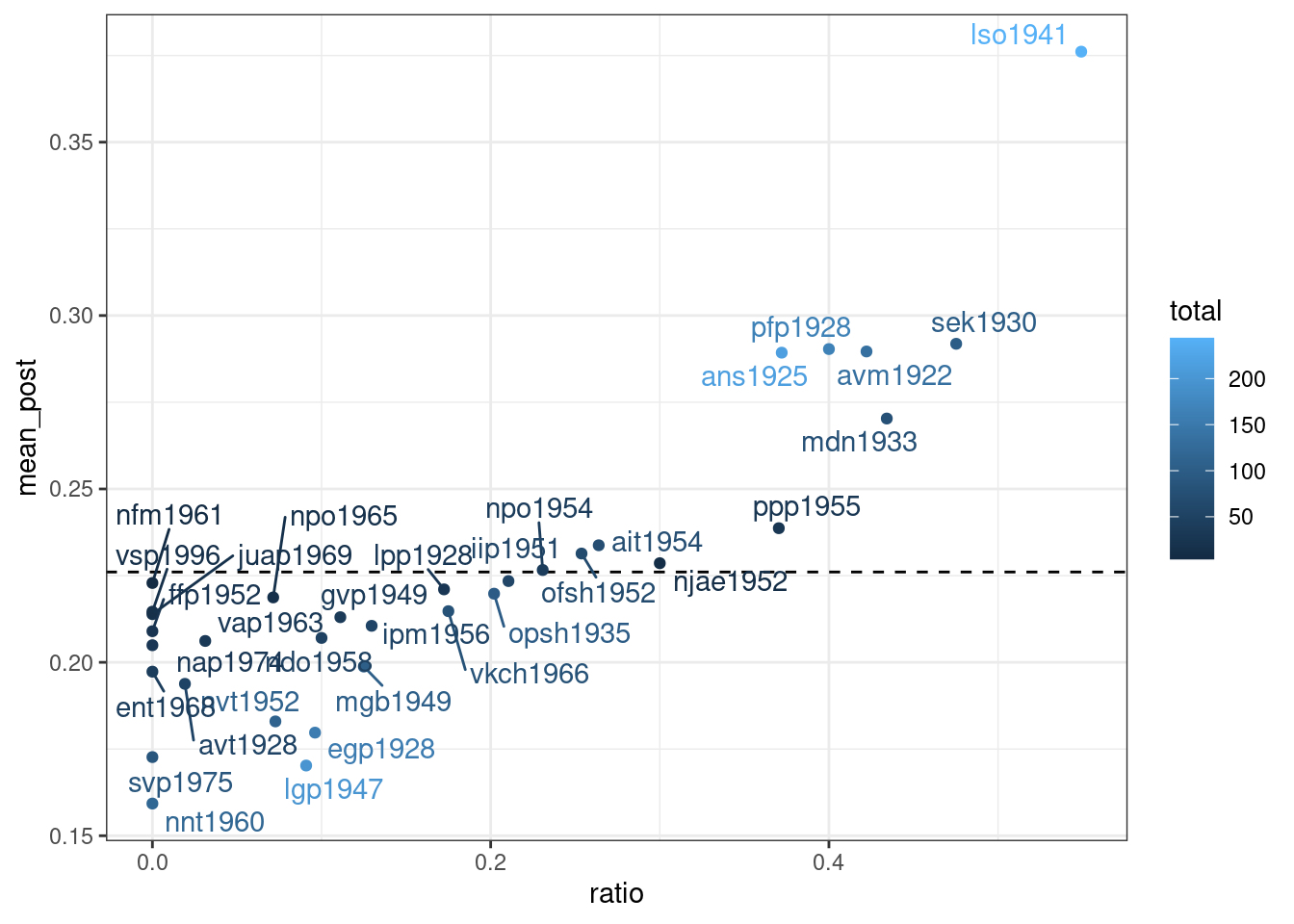

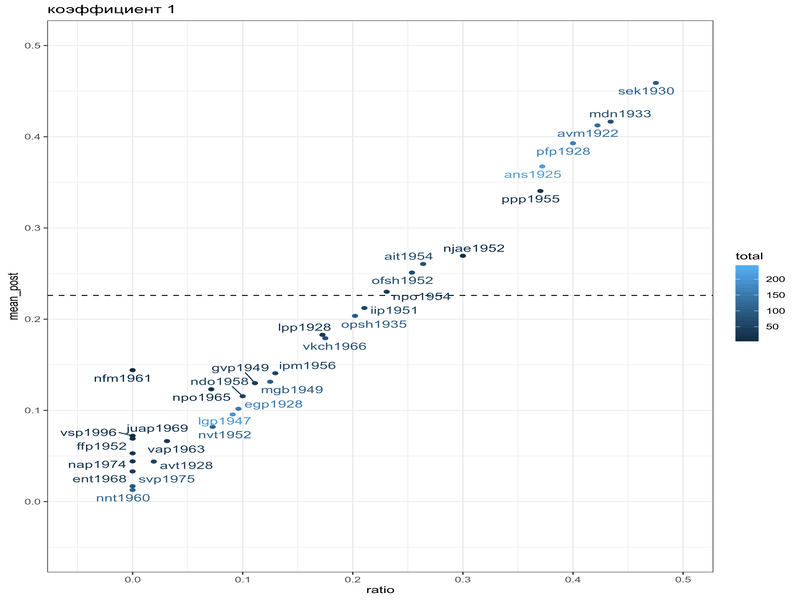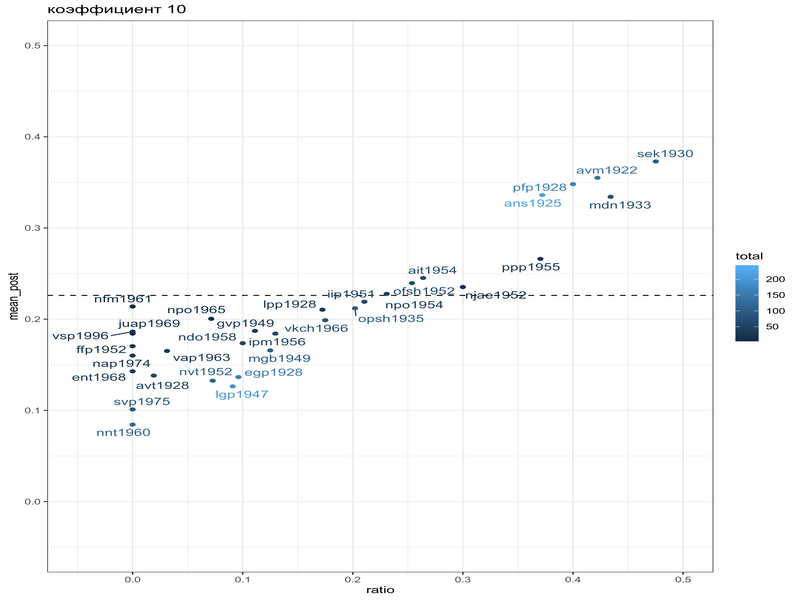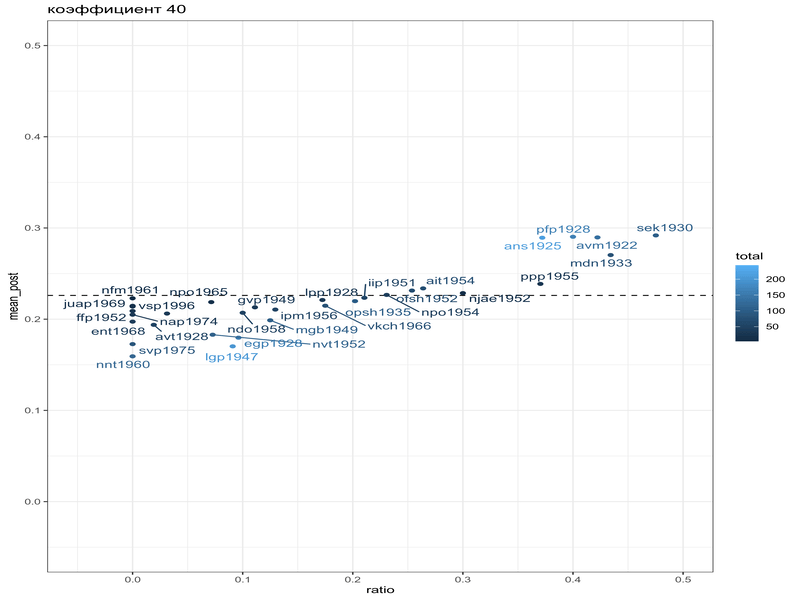
Или в формате гифки:

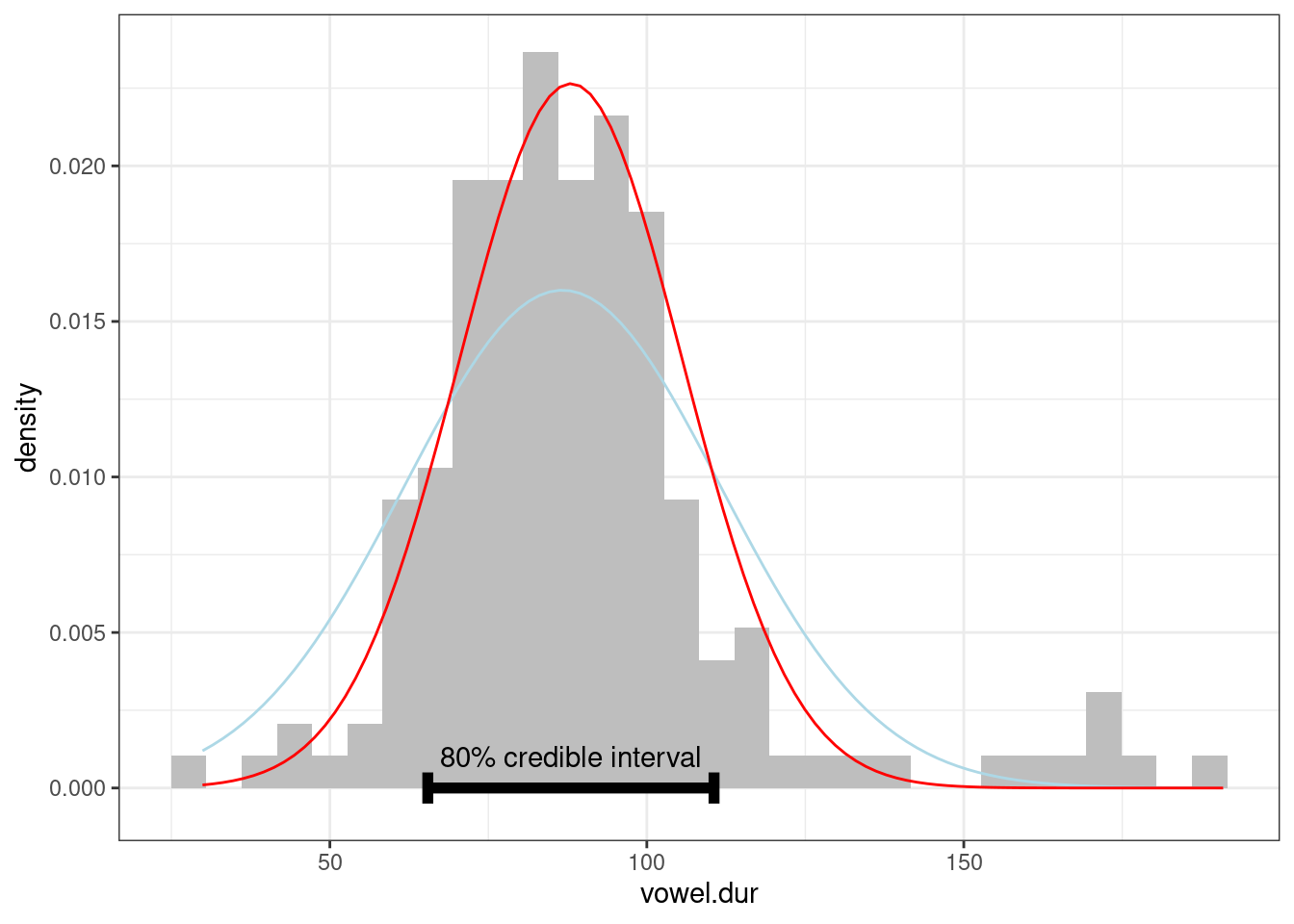
В работе (Coretta 2016) собраны данные длительности исландских гласных. Используя алгоритм максимального правдоподобия и идеи эмперической байесовской оценки, найдите априорное распределение для длительности гласных (переменная vowel.dur), используя все наблюдения в датасете и моделируя его нормальным распределением. Дальше проведите байесовский апдейт длительности гласных носителя tt01 (переменная speaker) и нарисуйте 80% доверительный интервал апостериорного распределения.

Ссылки на литературу

Coretta, Stefano. 2016. “Vowel Duration and Aspiration Effects in Icelandic.” University of York.

Daniel, Michael, Ruprecht von Waldenfels, Aleksandra Ter-Avanesova, Polina Kazakova, Ilya Schurov, Ekaterina Gerasimenko, Daria Ignatenko, et al. 2019. “Dialect Loss in the Russian North: Modeling Change Across Variables.” Language Variation and Change 31 (3): 353–76. https://doi.org/10.1017/S0954394519000243.