8 Основы статистического анализа

library(tidyverse)

8.1 О статистике

Статистика имеет большое значение в науке, и все чаще она позволяет принимать решения правительствам, корпорациям и т. п. В области принятия решений статистику сейчас теснят методы машинного обучения, однако в науке все же статистика продолжает занимать важное место, помогая подтвердить обнаруженные факты, принимать решения на основе данных и делать предсказания.

Важно подчеркнуть разницу между статистикой и машинным обучением: она заключается в основных целях. Статистика в основном занимается выводами и моделированием процессов, которые генерируют наблюдаемые данные, в то время как машинное обучение фокусируется на поиске обобщаемых предиктивных закономерностей в данных. Несмотря на то, что некоторые методы используются как в статистике, так и в машинном обучении, все же эти две области имеют разные цели и подходы.

Важно помнить, что статистика позволяет лишь моделировать процессы, которые стоят за генерацией данных. В связи с этим не стоит считать, что статистический вывод позволяет узнать правду или сделать правильный выбор: правильность и истинность любого конкретного случая зависит от научных установок исследователя, ответственного применения методов с соблюдением всех ограничений на их применение, качества сбора данных и теоретического обоснования процедуры анализа. Я призываю смотреть на статистику как на инструмент, который помогает в принятии решений, предсказании и моделировании: если вы забили шуруп молотком, то, вероятно, вашу задачу вы решили, но молоток сам по себе не несет ответственности за результат.

Сейчас широко распространены две школы статистического анализа: фреквентисткий (еще можно встретить термин частотный) и байесовский. Разница между этими подходами заключается в их основных принципах. Частотный подход основан на оценке статистического параметра на основе частоты его появления в выборке, в то время как байесовский подход позволяет представить оценку статистического параметра как распределение вероятностей, соединяя априорные знания о предметной области и новые данные. Фреквентистские методы получили широкое распространение в XX веке, а байесовские методы применялись задолго до фреквентистских, однако с развитием вычислительных мощностей в XXI веке популярность байесовских методов растет. В данной главе мы будем опираться на фреквентистские методы, так как погружение в байесовские методы требует значительной подготовки.

8.2 Тест Стьюдента (t-тест)

Первый статистический метод, который обычно обсуждают в фреквентистской статистике — это тест Стьюдента. Основное его применение заключается в сравнении средних значений двух групп (двухвыборочный тест) или среднего одной группы с некоторым значением (одновыборочный тест). Среди возможных задач, которые можно решить при помощи теста Стьюдента:

оценить эффект нового лекарства по сравнению со старым;
оценить эффект нового метода обучения на результатах тестов групп студентов;
оценить отличие какого-нибудь параметра популяции (например, избыточного веса) по сравнению с нормой.

Теперь мы обсудим стандартную процедуру фреквентистской статистики. Допустим мы сравниваем средние двух групп А и B. Принято создавать две гипотезы:

\(H_0\) — (нулевая гипотеза) разница между группами не является статистически значимой, т. е. наблюдаемые данные происходят из одного ожидаемого распределения.
\(H_1\) — (альтернативная гипотеза) разница является статистически значимой, т. е. наблюдаемые данные не происходят из одного ожидаемого распределения.

Нулевая гипотеза — это гипотеза, которую каждый исследователь в случае успеха отвергнет и примет альтернативную. После применения статистического критерия (каждый критерий зависит от конкретного статистического теста, а выбор теста зависит от типа данных) исследователь считает вероятность наблюдения такого или более экстремального результат, если верна нулевая гипотеза (p-value, p-уровень значимости).

В тесте Стьюдента таким распределением является t-распредление. Распределение, которое напоминает нормальное распределение, но имеет более широкие края:

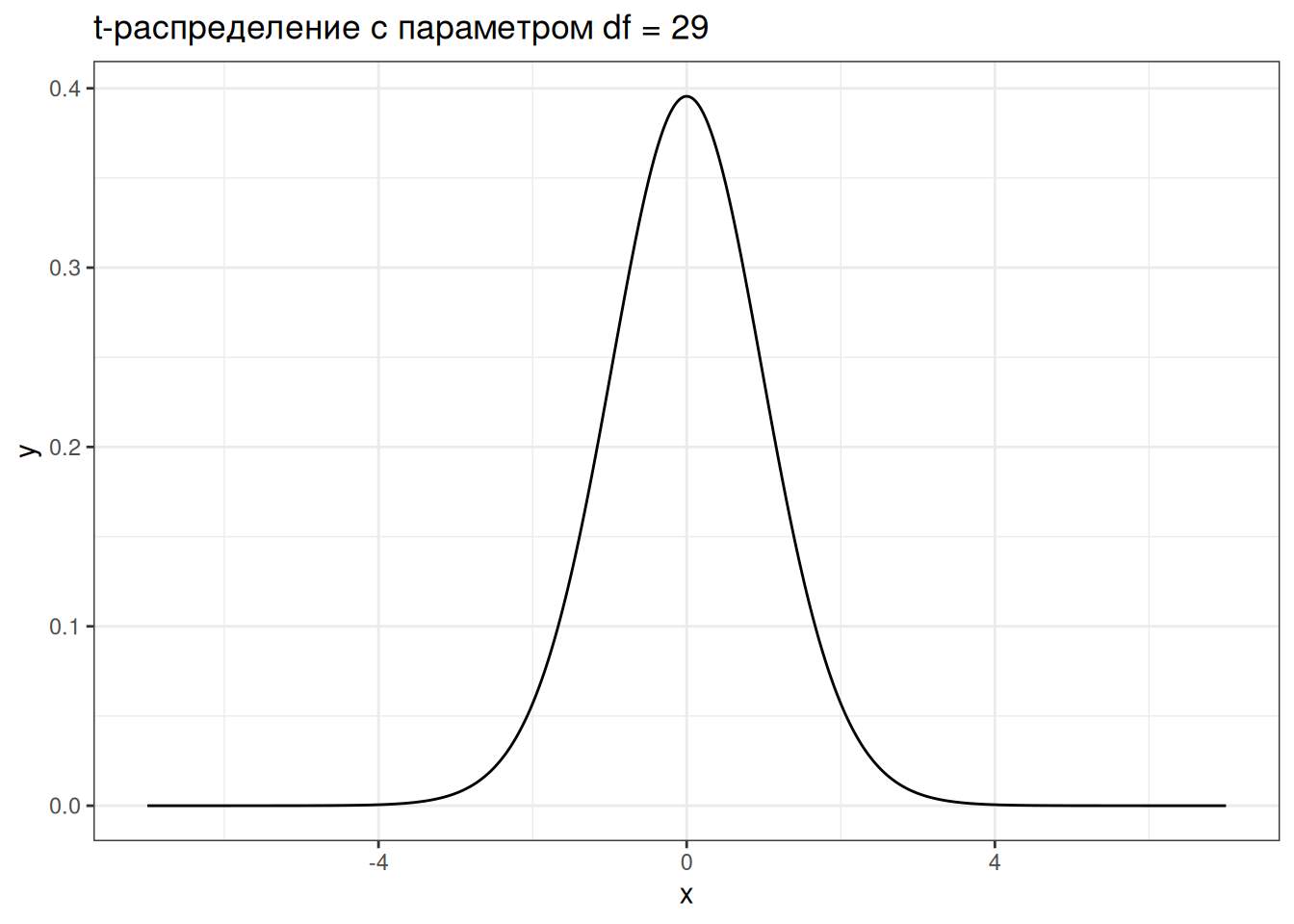
T-распределение имеет один параметр, который принято называть степенями свободы (degree of freedom, df). Чем больше степеней свободы, тем больше t-распределение похоже на нормальное распределение. Обычно этот параметр напрямую связывают с количеством наблюдений.

tibble(x = rep(seq(-7, 7, by = 0.01), 4),
       df = rep(c(5, 15, 30, 75), 1401),
       y = dt(x, df =df)) |> 
  ggplot(aes(x, y, color = as.factor(df)))+
  geom_line() + 
  labs(color = "")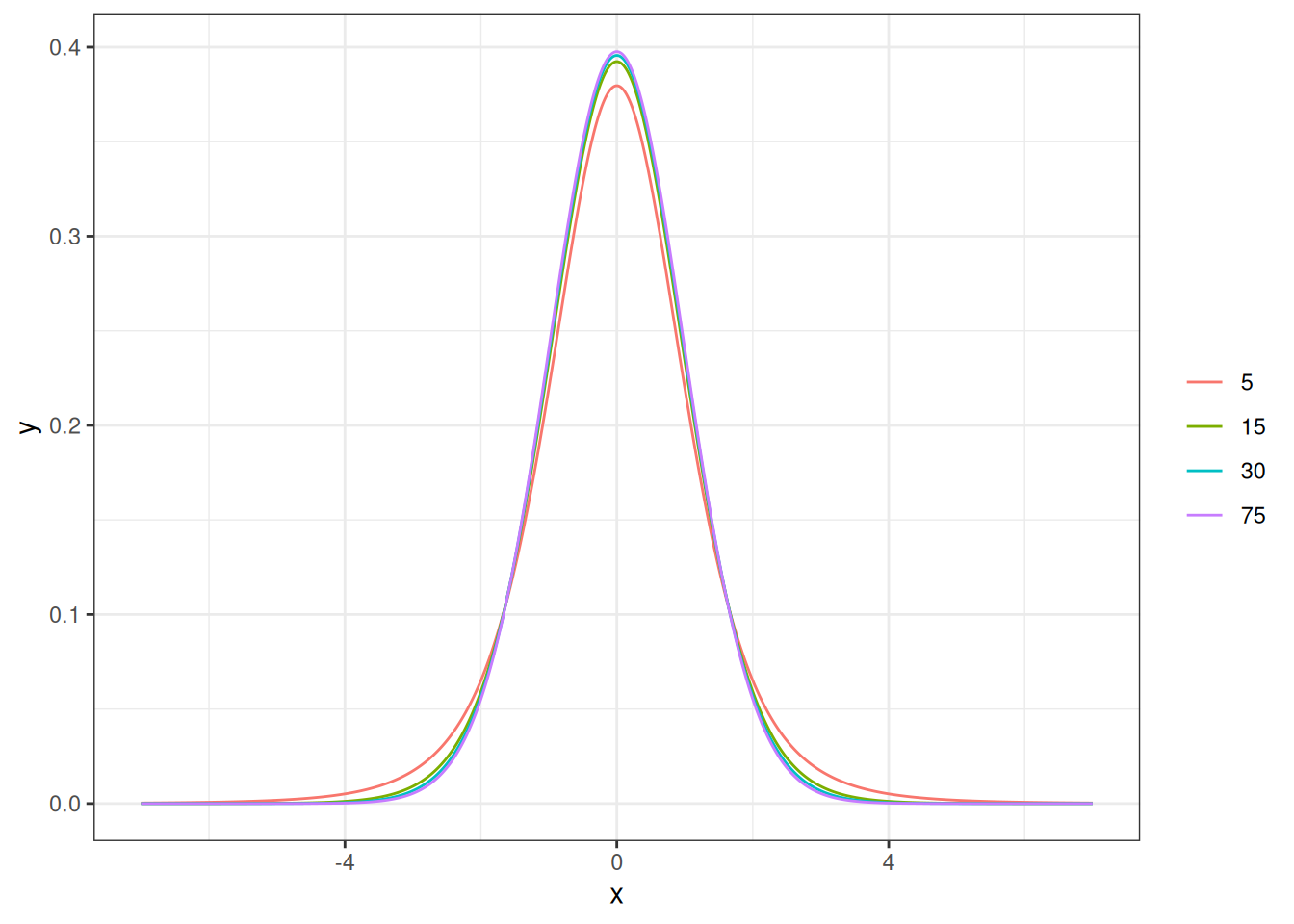

Давайте разберем на примере. Из статьи (Stepanova 2011) мы знаем, что носители русского языка в среднем говорят 5.31 слога в секунду со стандартным отклонением 1,93 (мужчины 5.46 слога в секунду со средним отклонением 2.02, женщины 5.23 слога в секунду со средним отклонением 1.84, дети 3.86 слога в секунду со средним отклонением 1.67). Мы опросили 30 носителей деревни N и выяснили, что среднее равно 7, а стандартное отклонение равно 2. Является ли данная разница статистически значимой? Рассмотрим данные

set.seed(42)

data <- rnorm(n = 30, mean = 7, sd = 2)

data

 [1]  9.741917  5.870604  7.726257  8.265725  7.808537  6.787751 10.023044
 [8]  6.810682 11.036847  6.874572  9.609739 11.573291  4.222279  6.442422
[15]  6.733357  8.271901  6.431494  1.687089  2.119066  9.640227  6.386723
[22]  3.437383  6.656165  9.429349 10.790387  6.139062  6.485461  3.473674
[29]  7.920195  5.720010

Вот так можно визуализировать наш вопрос:

tibble(data) |> 
  ggplot(aes(data))+
  geom_dotplot()+
  geom_vline(xintercept = mean(data), size = 2, linetype = 2)+
  geom_vline(xintercept = 5.31, size = 2, linetype = 2, color = "red")+
  annotate(geom = "text", x = 3, color = "red", y = 0.75, label = "среднее согласно\n[Stepanova 2011]", size = 5)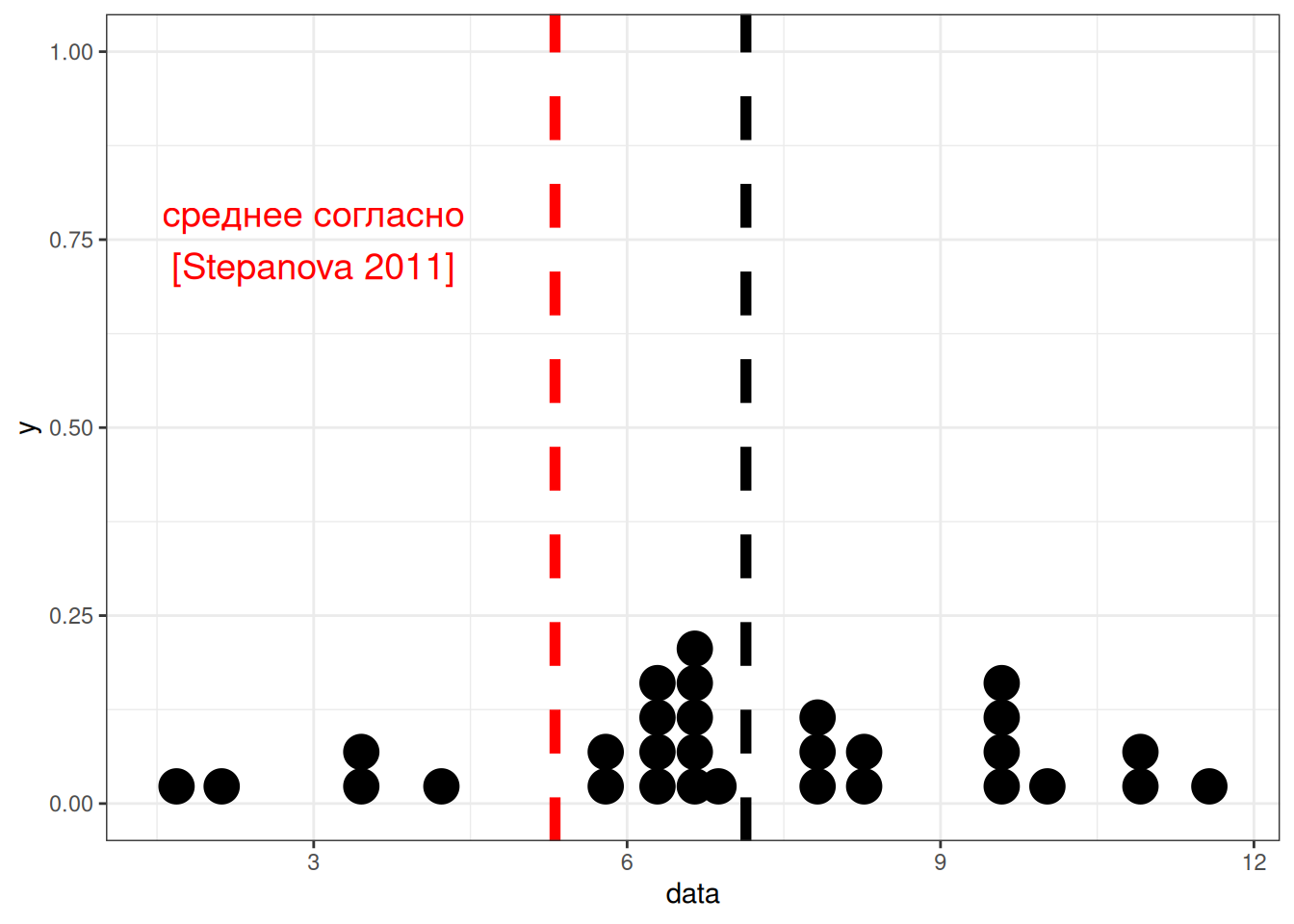

Применяем тест Стьюдента. Так как мы сравниваем нашу выборку с некоторым эталонным значением, мы применяем одновыборочный тест Стьюдента, а эталонное значение записываем в аргумент mu:

t.test(data, mu = 5.31)


    One Sample t-test

data:  data
t = 3.9871, df = 29, p-value = 0.0004143
alternative hypothesis: true mean is not equal to 5.31
95 percent confidence interval:
 6.199903 8.074444
sample estimates:
mean of x 
 7.137174

Если мы хотим визуализировать t-статистику, которую мы получили на t-распределении, получится вот такой график:

tibble(x = seq(-7, 7, by = 0.01),
       y = dt(x, df = 29)) |> 
  ggplot(aes(x, y))+
  geom_line()+
  geom_vline(linetype = 2, xintercept = 3.9871)+
  labs(title = "t-распределение с параметром df = 29")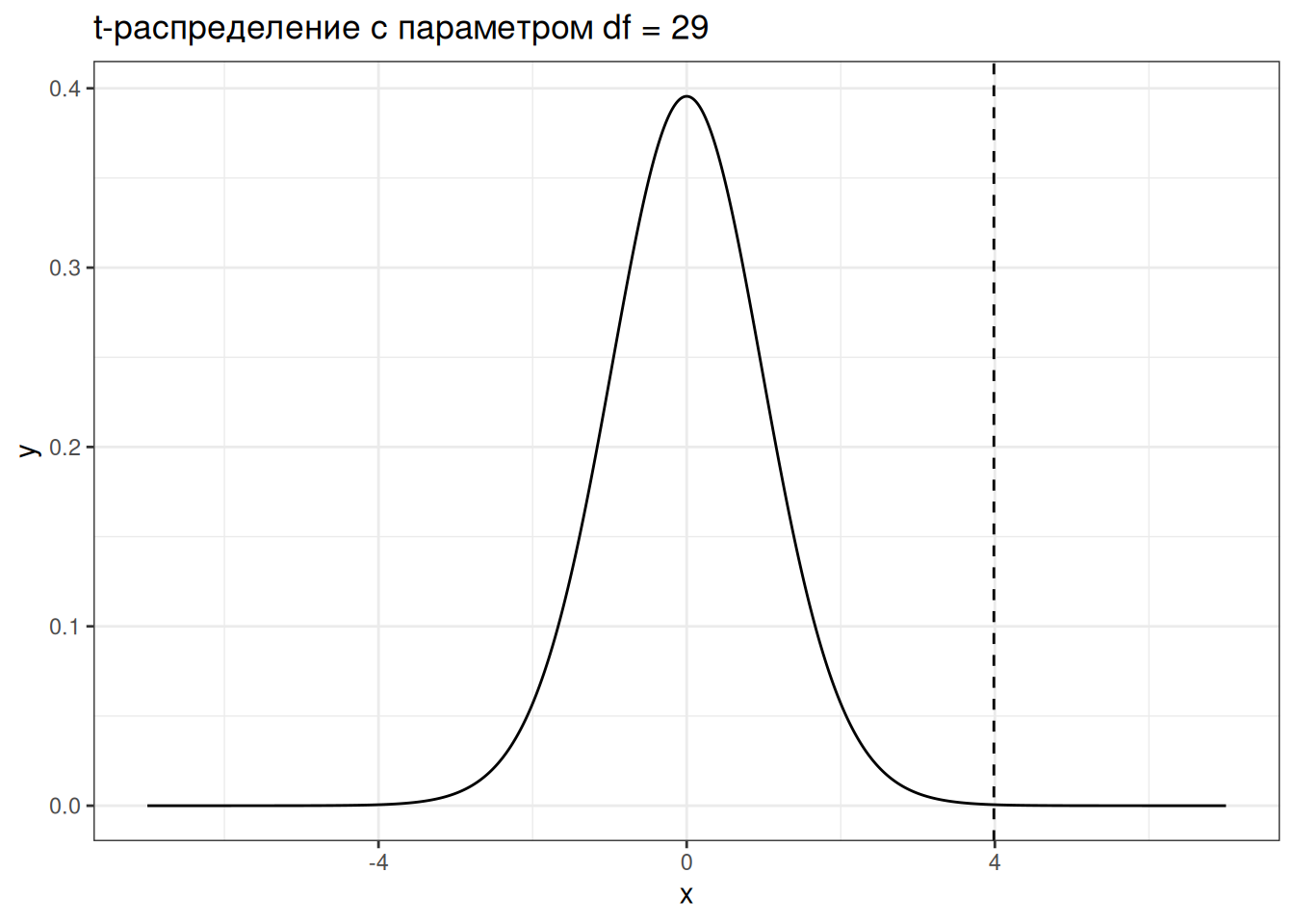

Если бы значение t-критерия оказалось где-то посередине, то тест Стьюдента бы выдал p-value больше 0.05 и тогда у нас бы не было оснований ни для отвержения, ни для принятия нулевой гипотезы.

8.2.1 Двухвыборочный тест Стьюдента

Логика двухвыборочного теста идентична логике одновыброчного, с тем лишь исключением, что мы сравниваем две группы:


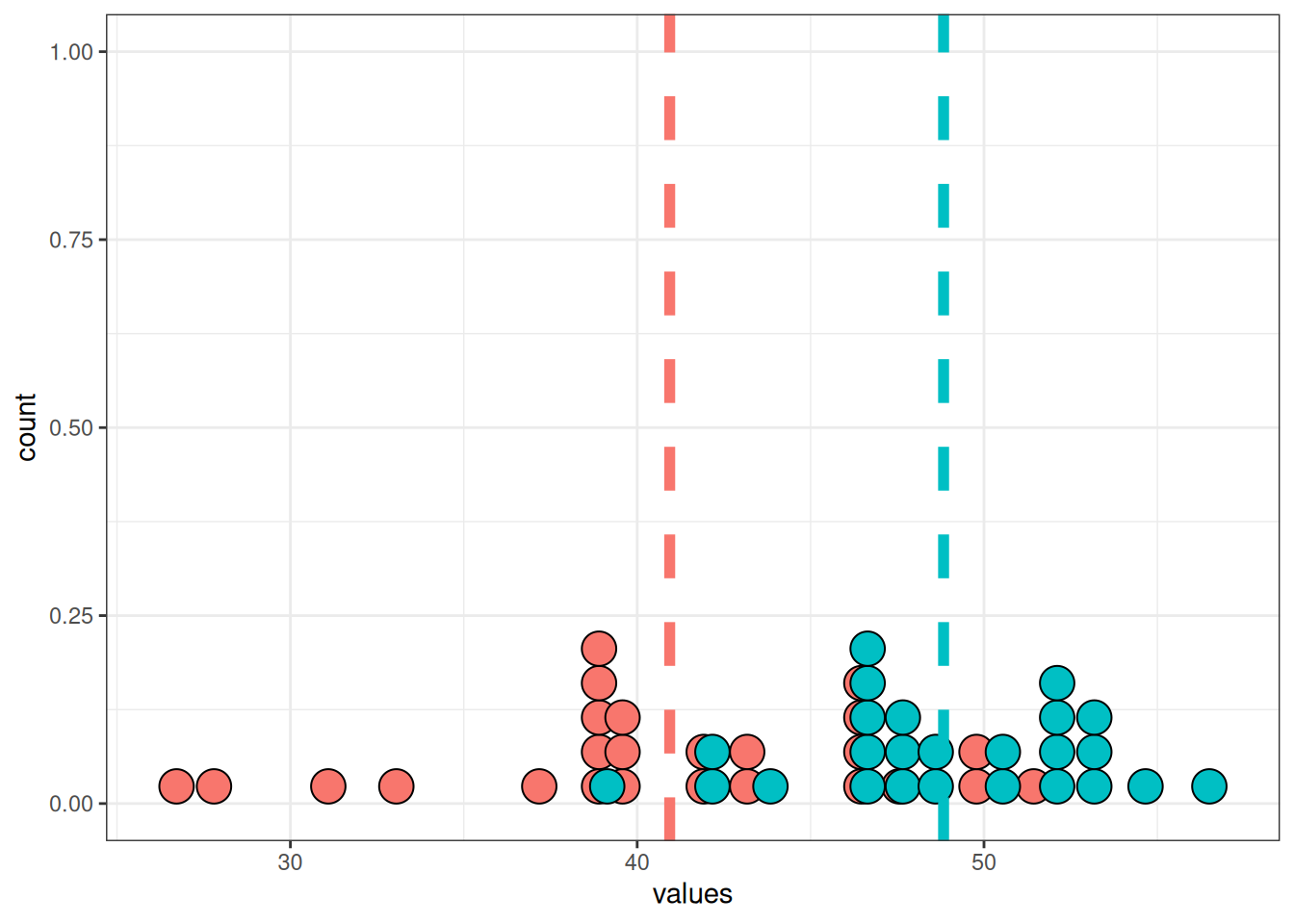
    Welch Two Sample t-test

data:  sample_1 and sample_2
t = -5.0632, df = 41.295, p-value = 9.005e-06
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -11.046695  -4.748026
sample estimates:
mean of x mean of y 
 40.93768  48.83504

На практике разница видна только в названии аргументов. Представим, что у нас есть две выборки:

sample_1

 [1] 46.85479 37.17651 41.81564 43.16431 42.02134 39.46938 47.55761 39.52670
 [9] 50.09212 39.68643 46.52435 51.43323 33.05570 38.60606 39.33339 43.17975
[17] 38.57874 26.71772 27.79767 46.60057 38.46681 31.09346 39.14041 46.07337
[25] 49.47597

sample_2

 [1] 48.06289 48.84229 42.06577 52.07044 47.12002 52.04953 53.17177 54.65797
 [9] 47.25983 52.27230 42.27346 46.46993 46.17092 39.13607 50.16255 50.92699
[17] 48.37524 53.41173 46.72983 43.84274 51.94768 46.34873 56.49846 48.05849
[25] 52.95042

Тогда для того, чтобы применить тест Стьюдента, нужно запустить следующий код:

t.test(sample_1, sample_2)


    Welch Two Sample t-test

data:  sample_1 and sample_2
t = -5.0632, df = 41.295, p-value = 9.005e-06
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
 -11.046695  -4.748026
sample estimates:
mean of x mean of y 
 40.93768  48.83504

8.3 Регрессионный анализ

8.3.1 Основы

Суть регрессионного анализа заключается в моделировании связи между двумя и более переменными при помощи прямой на плоскости. Формула прямой зависит от двух параметров: свободного члена (intercept) и углового коэффициента (slope).

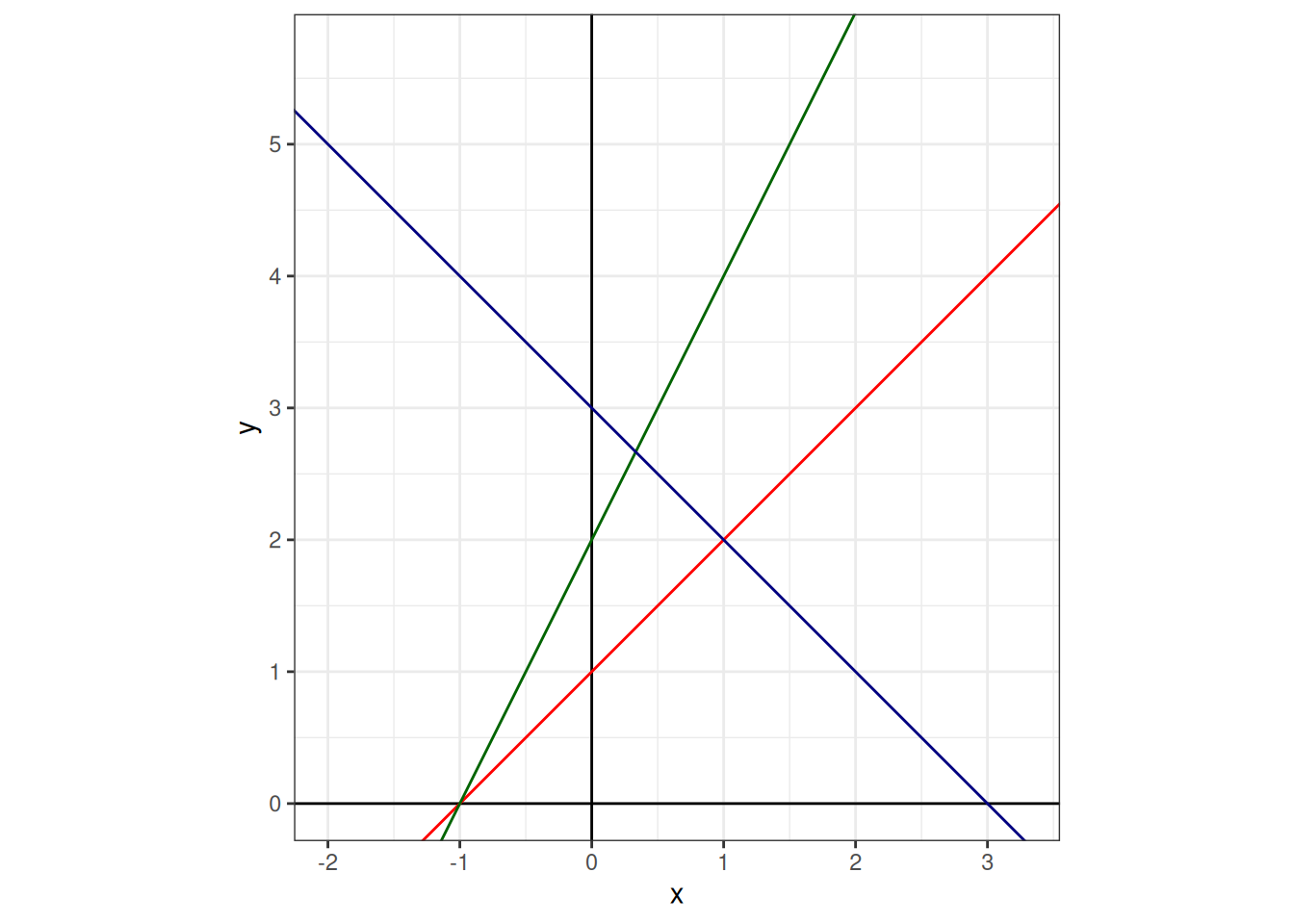
Когда мы пытаемся научиться предсказывать данные одной переменной \(Y\) при помощи другой переменной \(X\), мы получаем похожую формулу:

\[y_i = \hat\beta_0 + \hat\beta_1 \times x_i + \epsilon_i,\] где

\(x_i\) — \(i\)-ый элемент вектора значений \(X\);
\(y_i\) — \(i\)-ый элемент вектора значений \(Y\);
\(\hat\beta_0\) — оценка случайного члена (intercept);
\(\hat\beta_1\) — оценка углового коэффициента (slope);
\(\epsilon_i\) — \(i\)-ый остаток, разница между оценкой модели (\(\hat\beta_0 + \hat\beta_1 \times x_i\)) и реальным значением \(y_i\); весь вектор остатков иногда называют случайным шумом (на графике выделены красным).

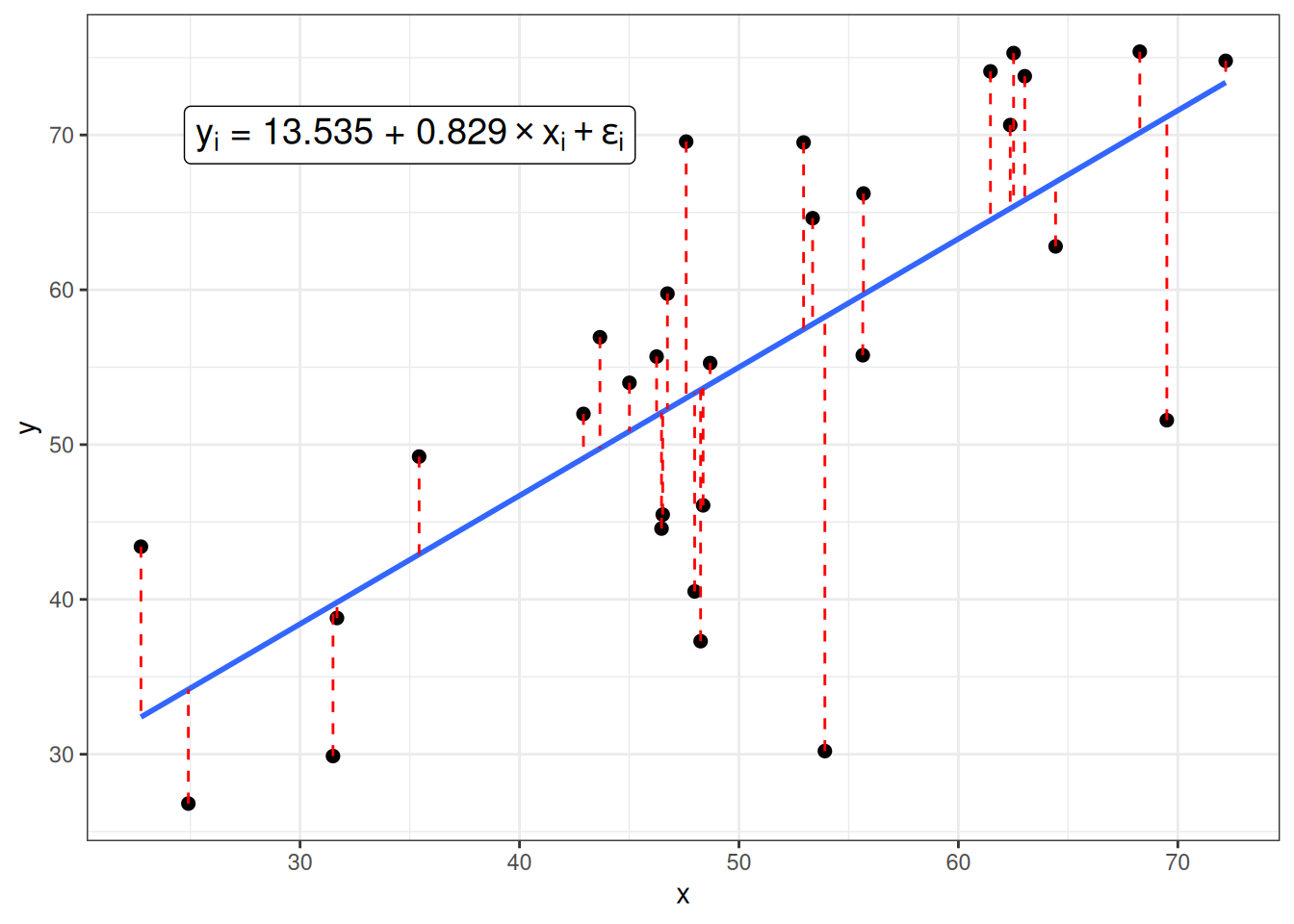
Задача регрессии — оценить параметры \(\hat\beta_0\) и \(\hat\beta_1\), если нам известны все значения \(x_i\) и \(y_i\) и мы пытаемся минимизировать значения \(\epsilon_i\). В данном случае, задачу можно решить аналитически и получить следующие формулы:

\[\hat\beta_1 = \frac{(\sum_{i=1}^n x_i\times y_i)-n\times\bar x \times \bar y}{\sum_{i = 1}^n(x_i-\bar x)^2}\]

\[\hat\beta_0 = \bar y - \hat\beta_1\times\bar x\]

8.3.2 Первая регрессия

Давайте попробуем смоделировать количество слов и в рассказах М. Зощенко в зависимости от длины рассказа:

zoshenko <- read_csv("https://raw.githubusercontent.com/agricolamz/daR4hs/main/data/w8_tidy_zoshenko.csv")

zoshenko |> 
  filter(word == "и") |> 
  distinct() ->
  zoshenko_filtered

zoshenko_filtered |>   
  ggplot(aes(n_words, n))+
  geom_point()+
  labs(x = "количество слов в рассказе",
       y = "количество и")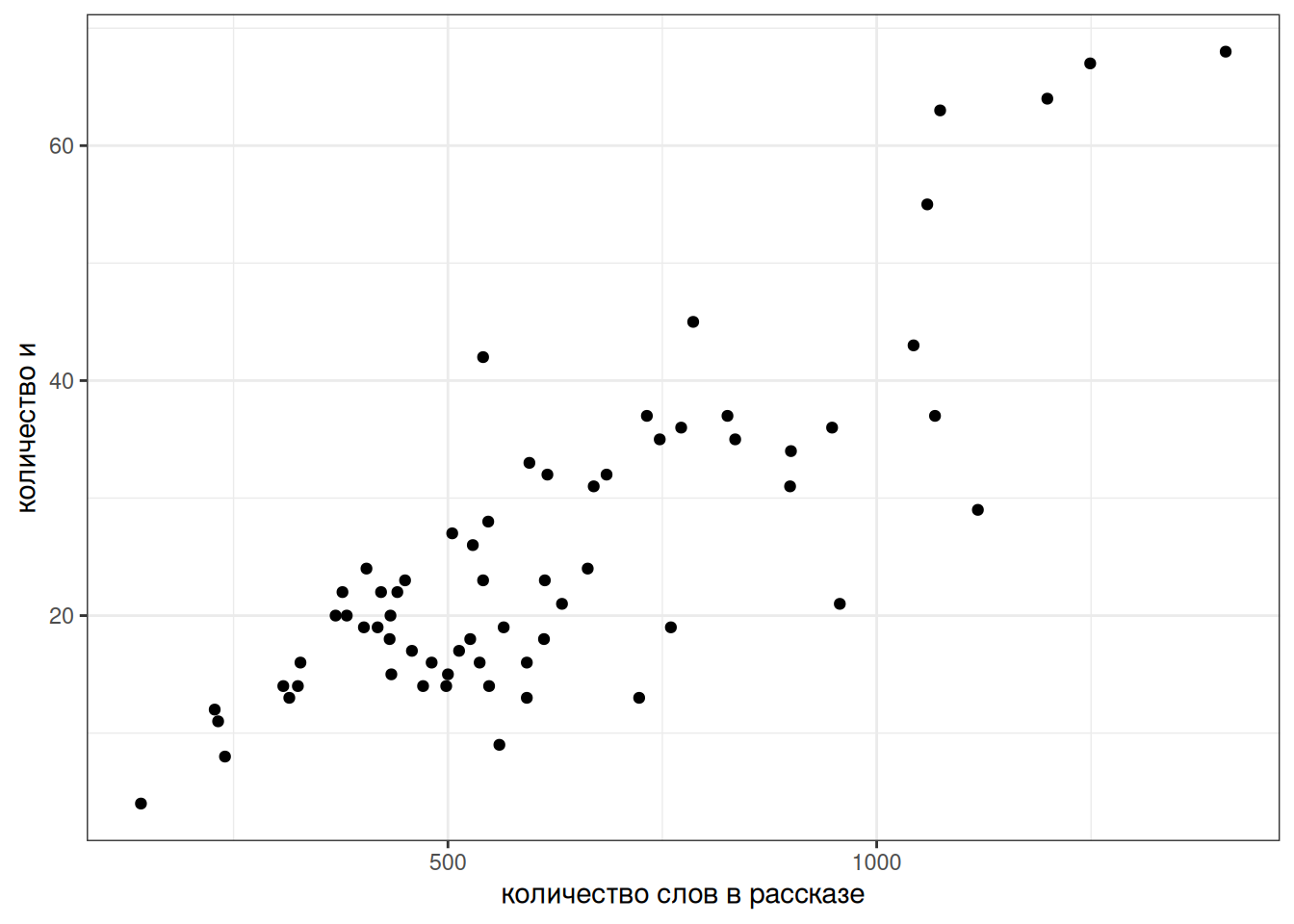

Давайте избавимся от них и добавим регрессионную линию при помощи функции geom_smooth():

zoshenko_filtered |> 
  ggplot(aes(n_words, n))+
  geom_point()+
  geom_smooth(method = "lm", se = FALSE)+
  labs(x = "количество слов в рассказе",
       y = "количество и")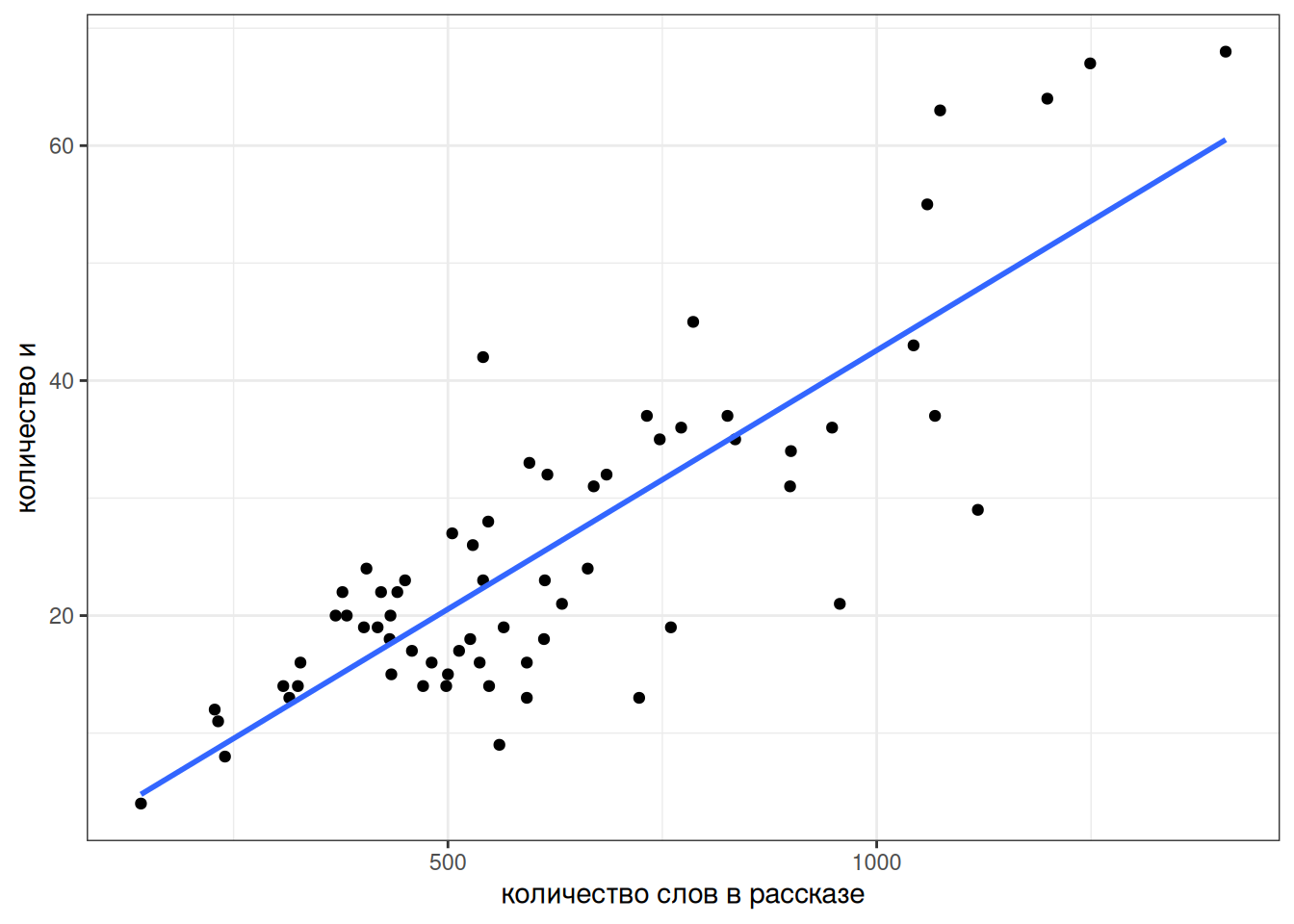

Чтобы получить формулу этой линии нужно запустить функцию, которая оценивает линейную регрессию:

fit <- lm(n~n_words, data = zoshenko_filtered)
fit


Call:
lm(formula = n ~ n_words, data = zoshenko_filtered)

Coefficients:
(Intercept)      n_words  
   -1.47184      0.04405

Вот мы и получили коэффициенты, теперь мы видим, что наша модель считает следующее:

\[n = -1.47184 + 0.04405 \times n\_words\]

Более подробную информацию можно посмотреть, если запустить модель в функцию summary():

summary(fit)


Call:
lm(formula = n ~ n_words, data = zoshenko_filtered)

Residuals:
     Min       1Q   Median       3Q      Max 
-19.6830  -4.3835   0.8986   4.6486  19.6413 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1.471840   2.467149  -0.597    0.553    
n_words      0.044049   0.003666  12.015   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 7.945 on 64 degrees of freedom
Multiple R-squared:  0.6928,    Adjusted R-squared:  0.688 
F-statistic: 144.4 on 1 and 64 DF,  p-value: < 2.2e-16

В разделе Coefficients содержится информацию про наши коэффициенты:

Estimate – полученная оценка коэффициентов;
Std. Error – стандартная ошибка среднего;
t value – \(t\)-статистика, полученная при проведении одновыборочного \(t\)-теста, сравнивающего данный коэфициент с 0;
Pr(>|t|) – полученное \(p\)-значение;
Multiple R-squared и Adjusted R-squared — одна из оценок модели, показывает связь между переменными. Без поправок совпадает с квадратом коэффициента корреляции Пирсона.
F-statistic — \(F\)-статистика полученная при проведении теста, проверяющего, не является ли хотя бы один из коэффицинтов статистически значимо отличным от нуля. Совпадает с результатами дисперсионного анализа (ANOVA).

Теперь мы можем даже предсказывать значения, которые мы еще не видели. Например, сколько будет и в рассказе Зощенко длиной 1000 слов?

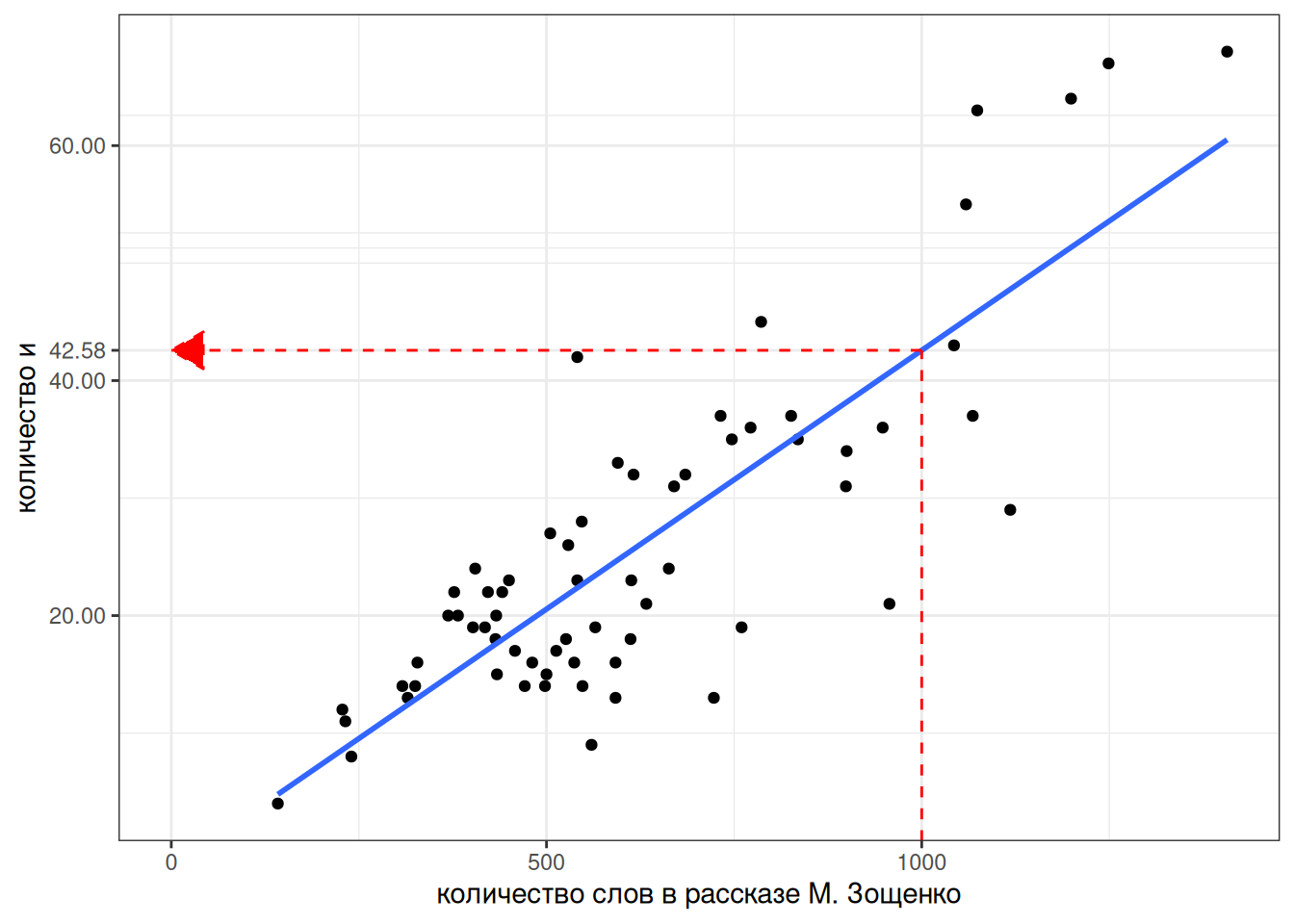
predict(fit, tibble(n_words = 1000))

       1 
42.57715

8.3.3 Категориальные переменные

Что если мы хотим включить в наш анализ категориальные переменные? Давайте рассмотрим простой пример с рассказами Чехова и Зощенко, которые мы рассматривали в прошлом разделе. Мы будем анализировать логарифм доли слова деньги:

chekhov <- read_csv("https://raw.githubusercontent.com/agricolamz/daR4hs/main/data/w8_tidy_chekhov.csv")
zoshenko <- read_csv("https://raw.githubusercontent.com/agricolamz/daR4hs/main/data/w8_tidy_zoshenko.csv")

chekhov |> 
  bind_rows(zoshenko) |> 
  filter(str_detect(word, "деньг")) |> 
  group_by(author, titles, n_words) |> 
  summarise(n = sum(n)) |> 
  mutate(log_ratio = log(n/n_words)) ->
  checkov_zoshenko

Визуализация выглядит так:

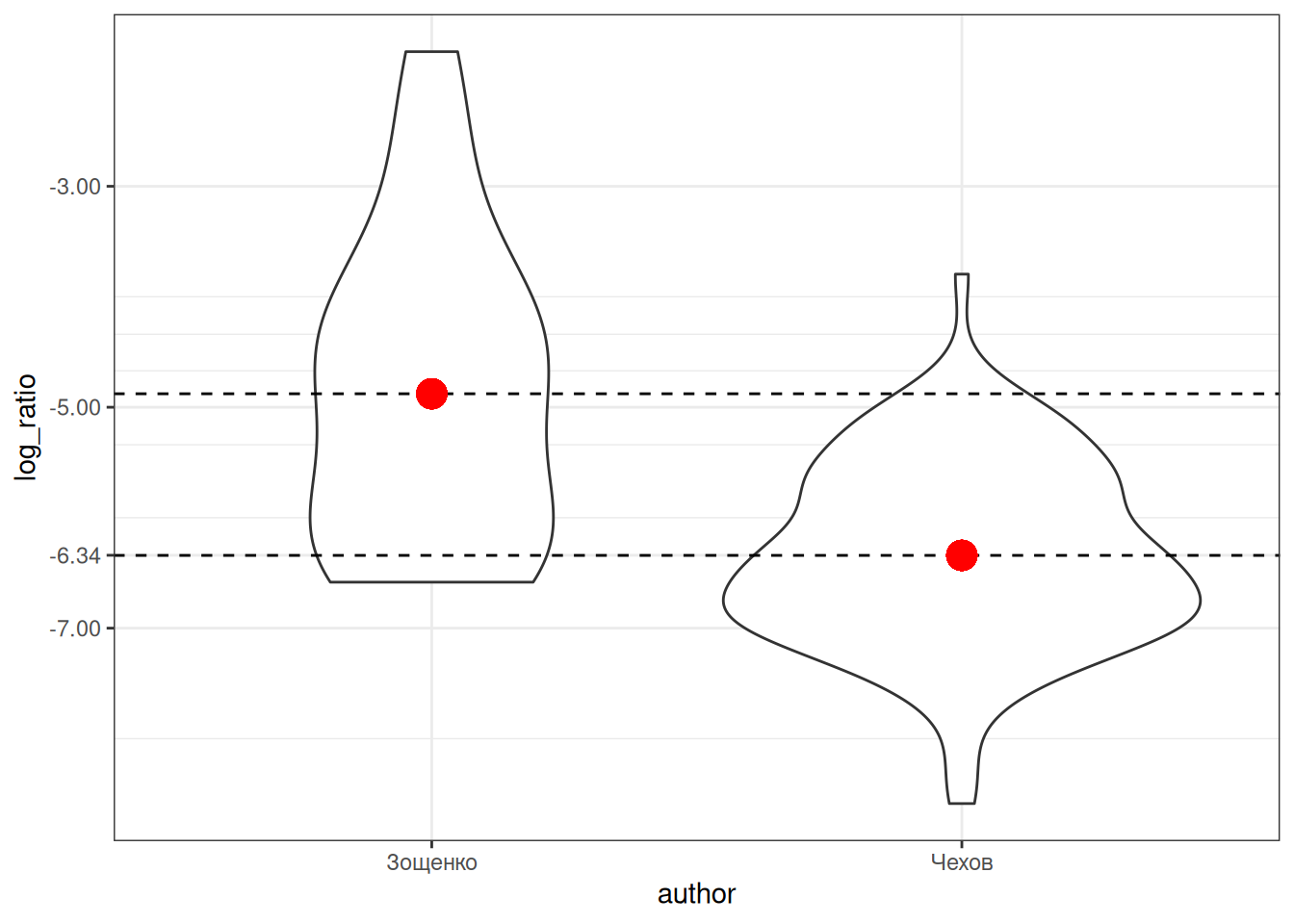
Красной точкой обозначены средние значения, так что мы видим, что между двумя писателями есть разница, но является ли она статистически значимой? В прошлом разделе мы рассмотрели, что в таком случае можно сделать t-test:

t.test(log_ratio~author, 
       data = checkov_zoshenko, 
       var.equal = TRUE) # здесь я мухлюю, отключая поправку Уэлча


    Two Sample t-test

data:  log_ratio by author
t = 6.3897, df = 124, p-value = 3.045e-09
alternative hypothesis: true difference in means between group Зощенко and group Чехов is not equal to 0
95 percent confidence interval:
 1.009976 1.916472
sample estimates:
mean in group Зощенко   mean in group Чехов 
            -4.878002             -6.341226

Разница между группами является статистически значимой (t(125) = 5.6871, p-value = 8.665e-08).

Для того, чтобы запустить регрессию на категориальных данных, категориальная переменная автоматически разбивается на группу бинарных dummy-переменных:

tibble(author = c("Чехов", "Зощенко"),
       dummy_chekhov = c(1, 0),
       dummy_zoshenko = c(0, 1))

Дальше для регрессионного анализа выкидывают одну из переменных, так как иначе модель не сойдется (dummy-переменных всегда n-1, где n — количество категорий в переменной).

tibble(author = c("Чехов", "Зощенко"),
       dummy_chekhov = c(1, 0))

Если переменная dummy_chekhov принимает значение 1, значит речь о рассказе Чехова, а если принимает значение 0, то о рассказе Зощенко. Если вставить нашу переменную в регрессионную формулу, получится следующее:

\[y_i = \hat\beta_0 + \hat\beta_1 \times \text{dummy\_chekhov} + \epsilon_i\]

Так как dummy_chekhov принимает либо значение 1, либо значение 0, то получается, что модель предсказывает лишь два значения:

\[y_i = \left\{\begin{array}{ll}\hat\beta_0 + \hat\beta_1 \times 1 + \epsilon_i = \hat\beta_0 + \hat\beta_1 + \epsilon_i\text{, если рассказ Чехова}\\ \hat\beta_0 + \hat\beta_1 \times 0 + \epsilon_i = \hat\beta_0 + \epsilon_i\text{, если рассказ Зощенко} \end{array}\right.\]

Таким образом, получается, что свободный член \(\beta_0\) и угловой коэффициент \(\beta_1\) в регрессии с категориальной переменной получают другую интерпретацию. Одно из значений переменной кодируется при помощи \(\beta_0\), а сумма коэффициентов \(\beta_0+\beta_1\) дает другое значение переменной. Так что \(\beta_1\) — это разница между оценками двух значений переменной.

Давайте теперь запустим регрессию на этих же данных:

fit2 <- lm(log_ratio~author, data = checkov_zoshenko)
summary(fit2)


Call:
lm(formula = log_ratio ~ author, data = checkov_zoshenko)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.24643 -0.61293 -0.05149  0.65130  3.09655 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   -4.878      0.210  -23.22  < 2e-16 ***
authorЧехов   -1.463      0.229   -6.39 3.05e-09 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.9393 on 124 degrees of freedom
Multiple R-squared:  0.2477,    Adjusted R-squared:  0.2416 
F-statistic: 40.83 on 1 and 124 DF,  p-value: 3.045e-09

Во-первых, стоит обратить внимание на то, что R сам преобразовал нашу категориальную переменную в dummy-переменную authorЧехов. Во-вторых, можно заметить, что значения t-статистики и p-value совпадают с результатами, полученными нами в t-тесте выше. Статистически значимый коэффициент при аргументе authorЧехов следует интерпретировать как разницу средних между логарифмом долей в рассказах Чехова и Зощенко.

8.3.4 Множественная регрессия

Множественная регрессия позволяет проанализировать связь между переменной и несколькими предикторами. Формула множественной регрессии не сильно отличается от формулы обычной линейной регрессии:

\[y_i = \hat\beta_0 + \hat\beta_1 \times x_{1i}+ \dots+ \hat\beta_n \times x_{ni} + \epsilon_i,\]

\(x_{ki}\) — \(i\)-ый элемент векторов значений \(X_1, \dots, X_n\);
\(y_i\) — \(i\)-ый элемент вектора значений \(Y\);
\(\hat\beta_0\) — оценка случайного члена (intercept);
\(\hat\beta_k\) — коэфциент при переменной \(X_{k}\);
\(\epsilon_i\) — \(i\)-ый остаток, разница между оценкой модели (\(\hat\beta_0 + \hat\beta_1 \times x_i\)) и реальным значением \(y_i\); весь вектор остатков иногда называют случайным шумом.

В такой регрессии предикторы могут быть как числовыми, так и категориальными (со всеми вытекающими последствиями, которые мы обсудили в предыдущем разделе). Такую регрессию чаще всего сложно визуализировать, так как в одну регрессионную линию вкладываются сразу несколько переменных.

Попробуем предсказать длину лепестка на основе длины чашелистиков и вида ириса:

iris |> 
  ggplot(aes(Sepal.Length, Petal.Length, color = Species))+
  geom_point()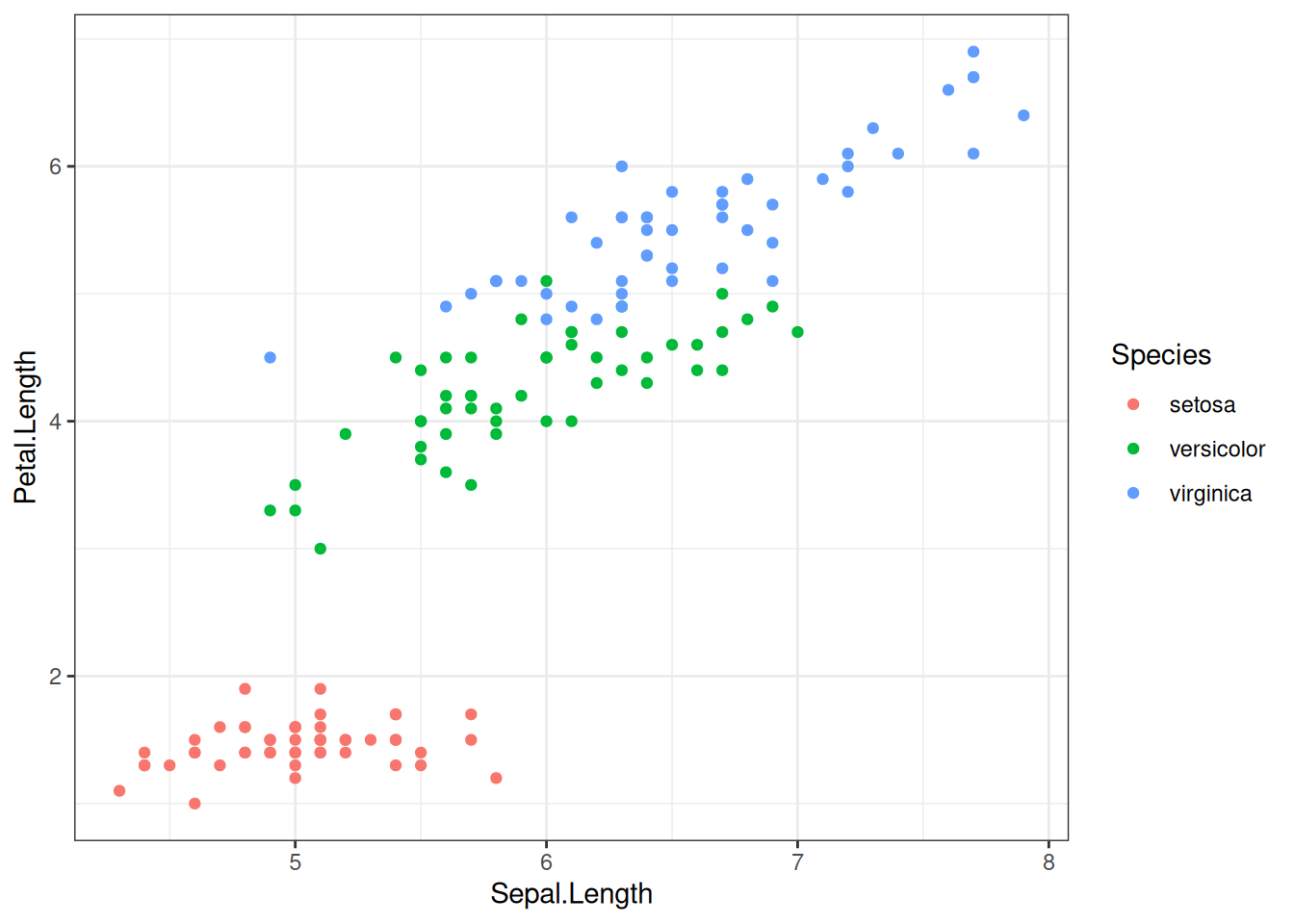

Запустим регрессию:

fit3 <- lm(Petal.Length ~ Sepal.Length + Species, data = iris)
summary(fit3)


Call:
lm(formula = Petal.Length ~ Sepal.Length + Species, data = iris)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.76390 -0.17875  0.00716  0.17461  0.79954 

Coefficients:
                  Estimate Std. Error t value Pr(>|t|)    
(Intercept)       -1.70234    0.23013  -7.397 1.01e-11 ***
Sepal.Length       0.63211    0.04527  13.962  < 2e-16 ***
Speciesversicolor  2.21014    0.07047  31.362  < 2e-16 ***
Speciesvirginica   3.09000    0.09123  33.870  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.2826 on 146 degrees of freedom
Multiple R-squared:  0.9749,    Adjusted R-squared:  0.9744 
F-statistic:  1890 on 3 and 146 DF,  p-value: < 2.2e-16

Все предикторы статистически значимы. Давайте посмотрим предсказания модели для всех наблюдений:

iris |> 
  mutate(prediction = predict(fit3)) |> 
  ggplot(aes(Sepal.Length, prediction, color = Species))+
  geom_point()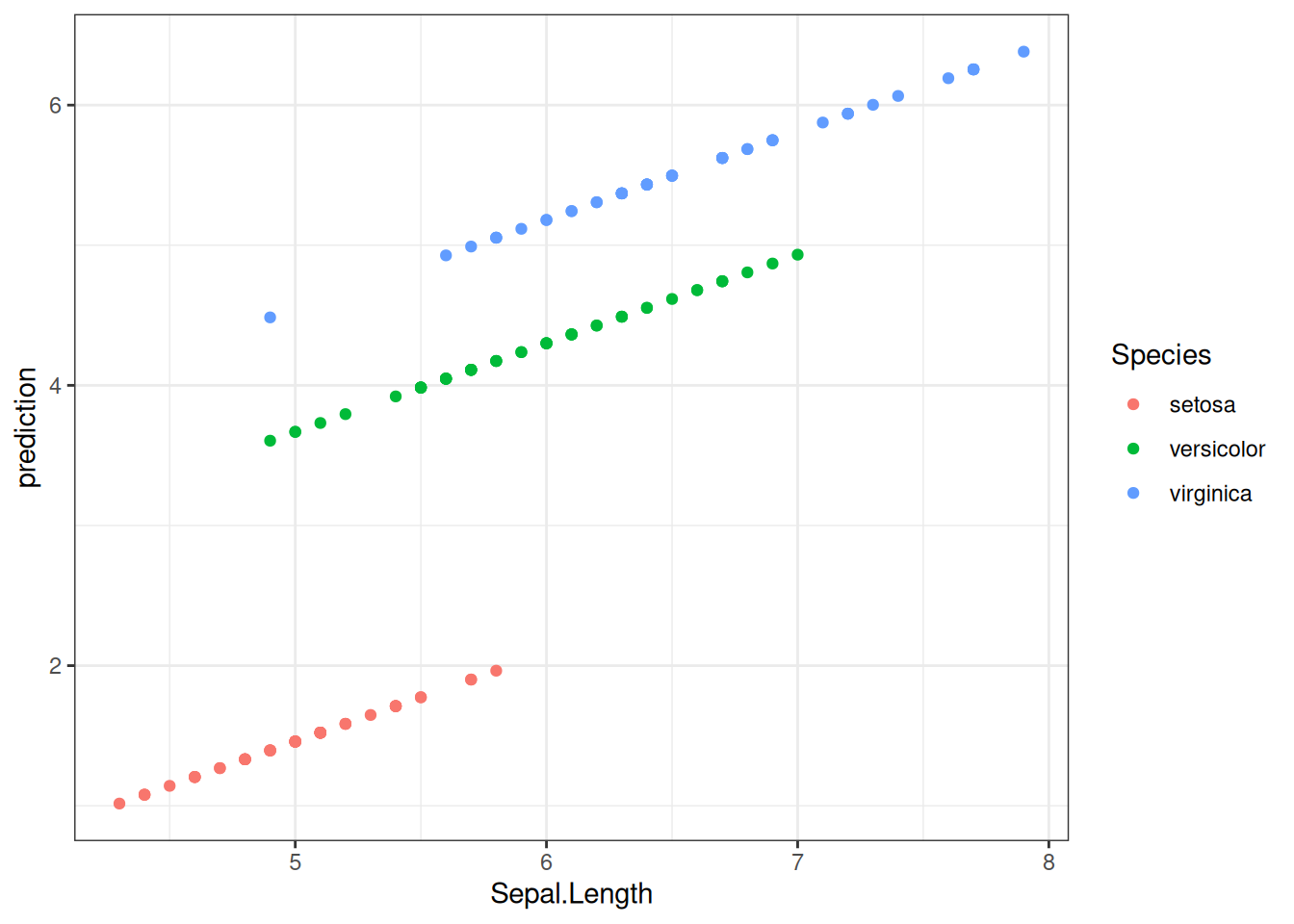

Всегда имеет смысл визуализировать, что нам говорит наша модель. Если использовать пакет ggeffects (или предшествовавший ему пакет effects), это можно сделать не сильно задумываясь, как это делать:

library(ggeffects)
plot(ggpredict(fit3, terms = c("Sepal.Length", "Species")))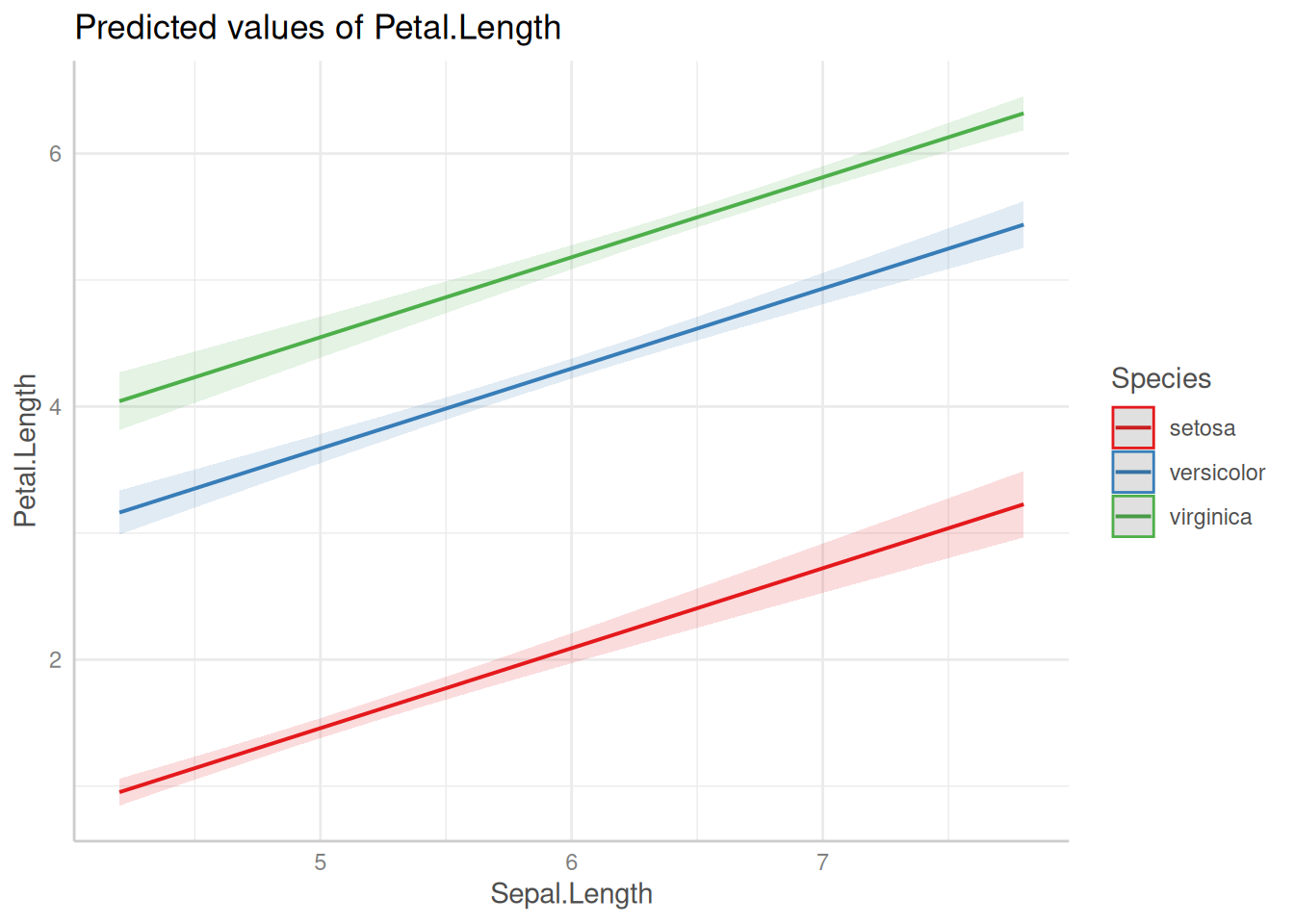

Как видно из графиков, наша модель имеет одинаковые угловые коэффициенты (slope) для каждого из видов ириса и разные свободные члены (intercept).

summary(fit3)


Call:
lm(formula = Petal.Length ~ Sepal.Length + Species, data = iris)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.76390 -0.17875  0.00716  0.17461  0.79954 

Coefficients:
                  Estimate Std. Error t value Pr(>|t|)    
(Intercept)       -1.70234    0.23013  -7.397 1.01e-11 ***
Sepal.Length       0.63211    0.04527  13.962  < 2e-16 ***
Speciesversicolor  2.21014    0.07047  31.362  < 2e-16 ***
Speciesvirginica   3.09000    0.09123  33.870  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.2826 on 146 degrees of freedom
Multiple R-squared:  0.9749,    Adjusted R-squared:  0.9744 
F-statistic:  1890 on 3 and 146 DF,  p-value: < 2.2e-16

\[y_i = \left\{\begin{array}{ll} -1.70234 + 0.63211 \times \text{Sepal.Length} + \epsilon_i\text{, если вид setosa}\\ -1.70234 + 2.2101 + 0.63211 \times \text{Sepal.Length} + \epsilon_i\text{, если вид versicolor} \\ -1.70234 + 3.09 + 0.63211 \times \text{Sepal.Length} + \epsilon_i\text{, если вид virginica} \end{array}\right.\]

8.3.5 Сравнение моделей

Как нам решить, какая модель лучше? Ведь теперь можно добавить сколько угодно предикторов? Давайте создадим новую модель без предиктора Species:

fit4 <- lm(Petal.Length ~ Sepal.Length, data = iris)

можно сравнивать статистическую значимость предикторов
можно сравнивать \(R^2\)

summary(fit3)$adj.r.squared

[1] 0.9743786

summary(fit4)$adj.r.squared

[1] 0.7583327

чаще всего используют так называемые информационные критерии, самый популярный – AIC (Akaike information criterion). Само по себе значение этого критерия не имеет смысла – только в сравнении моделей, построенных на похожих данных. Чем меньше значение, тем модель лучше.

AIC(fit3, fit4)

8.3.6 Послесловие

существуют ограничения на применение линейной регрессии
- связь между предсказываемой переменной и предикторами должна быть линейной
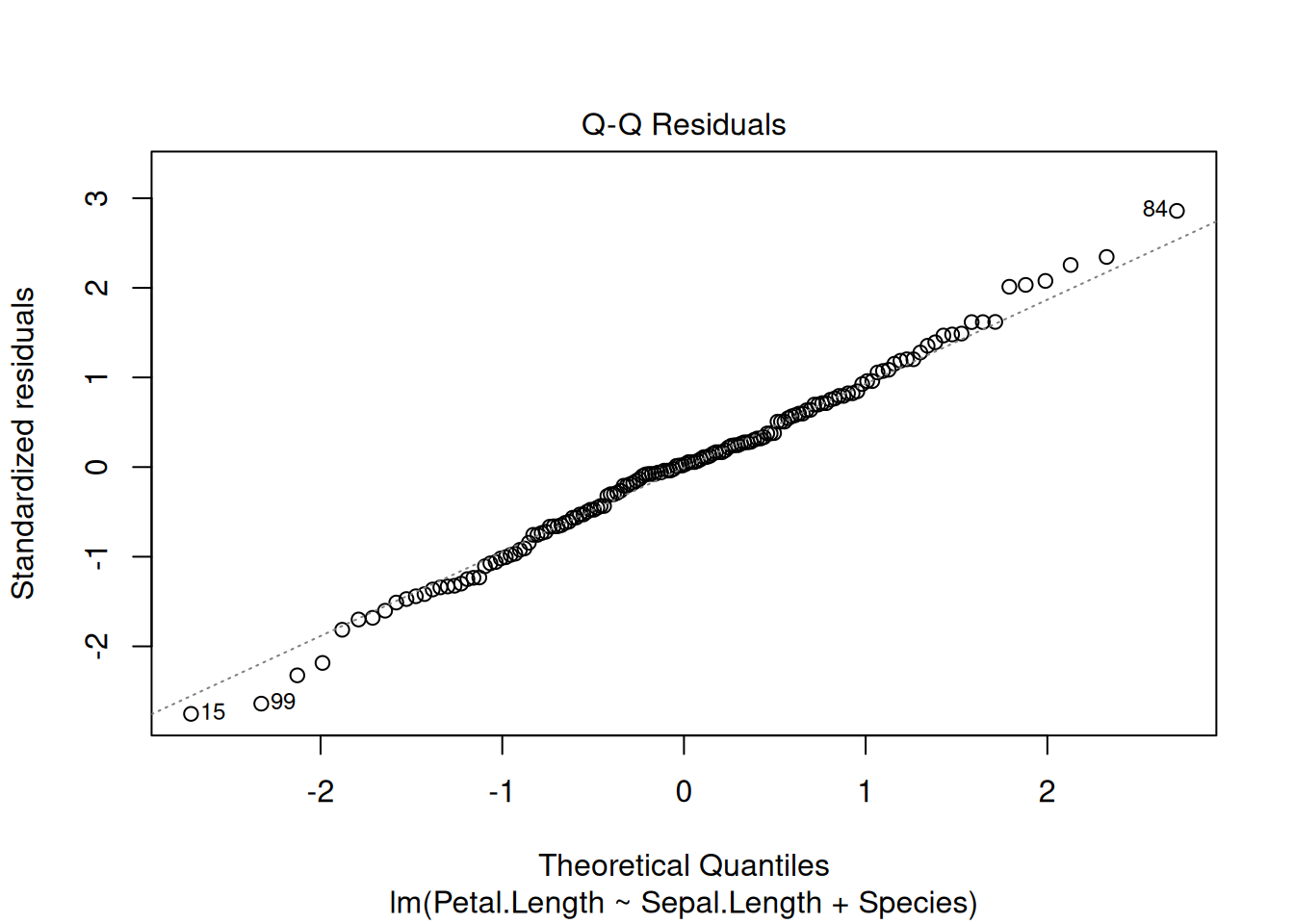
- остатки должны быть нормально распределены (оценивайте визуально)
- дисперсия остатков вокруг регрессионной линии должна быть постоянна (гомоскедастичность)
- предикторы не должны коррелировать друг с другом
- все наблюдения в регрессии должны быть независимы друг от друга

Вот так вот выглядят остатки нашей модели на основе датасета iris. Смотрите пост, в котором обсуждается, как интерпретировать график остатков.

plot(fit3, which=c(1, 2))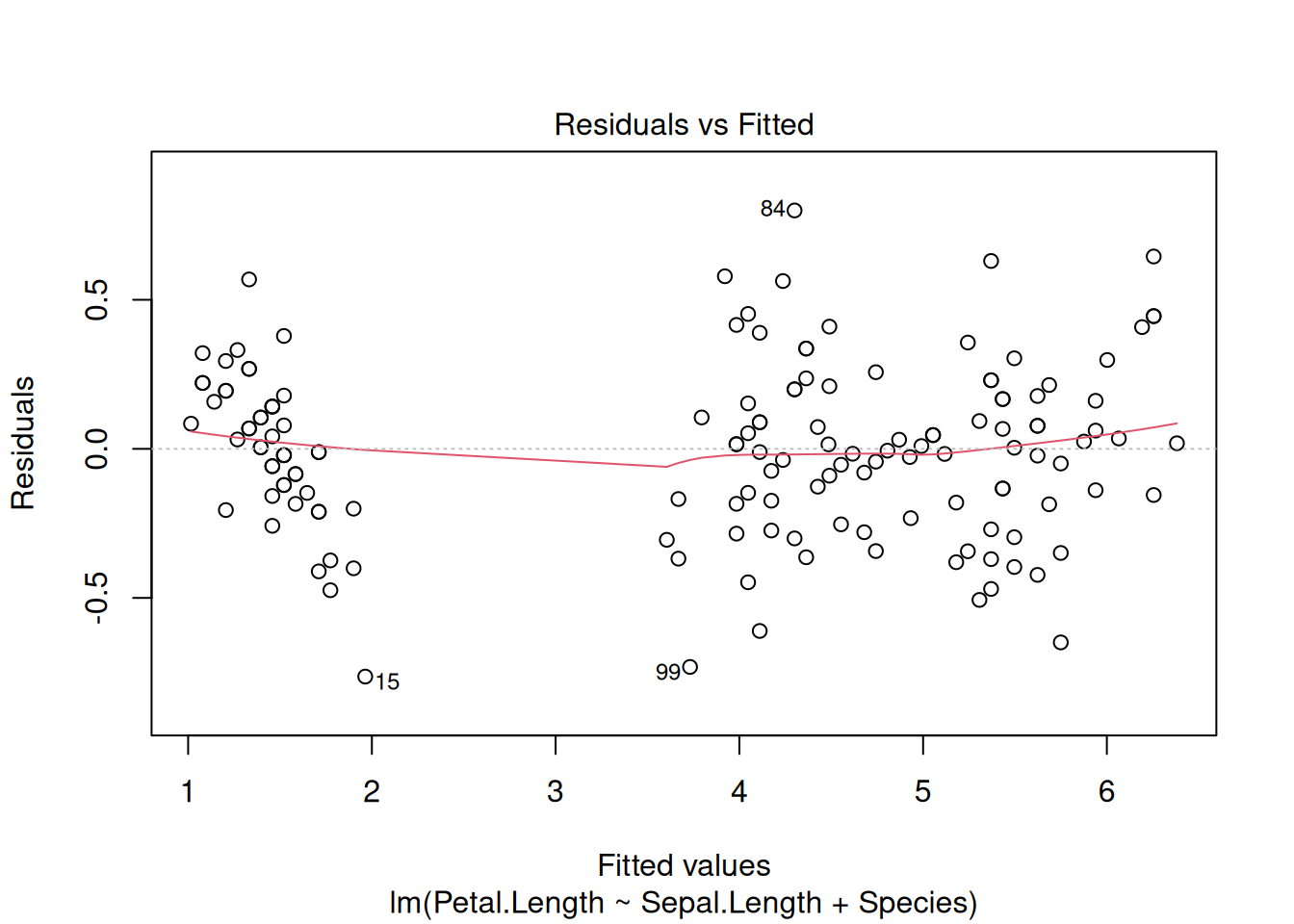

существуют трюки, позволяющие автоматически отбирать модели (см. функцию step())
существует достаточно большое семейство регрессий, которые зависят от типа независимой (предсказываемой) переменной или ее распределения
- логистическая (если предсказываемая переменная имеет два возможных исхода)
- мультиномиальная (если предсказываемая переменная имеет больше двух возможных дискретных исходов)
- нелинейные регрессии (если связь между переменными нелинейна)
- регрессия со смешанными эффектами (если внутри данных есть группировки, т. е. наблюдения не независимы)
- и другие.