1. Гармонические колебания, преобразование Фурье

Для тех, кто хочет следить за кодом, вот загруженные библиотеки:

library(tidyverse)
# это стиль для ggplot (можно игнорировать эту команду)
theme_set(theme_bw()+
            theme(text = element_text(size = 16)))

1.1 Гармонические колебания, их представления и их свойства

1.1.1 Гармонические колебания

Переодическое колебание — тип колебания, при котором значения параметров колебательной системы (амплитуда, период, частота) повторяются через равные промежутки времени. Примером такого колебания могут быть колебания маятников, струн, частиц воздуха и т. п.

Фрагмента графика простого гармонического коллебания:

tibble(t = seq(0, 7*pi, by = 0.001),
       y = sin(t)) %>% 
  ggplot(aes(t, y))+
  geom_line()+
  geom_hline(yintercept = 0, linetype = 2)+
  labs(caption = "sin(x)")

🤔 Почему фрагмент? Потому что идеальное гармоническое колебание не имеет ни начала ни конца. Реальные волны, представленые в мире все квазипереодические.

Фрагмента графика другого гармонического коллебания:

tibble(t = seq(0, 7*pi, by = 0.001),
       y = sin(t)+sin(2*t)) %>% 
  ggplot(aes(t, y))+
  geom_line()+
  geom_hline(yintercept = 0, linetype = 2)+
  labs(caption = "sin(x)+sin(2*x)")

Периодические колебания обычно имеют некоторую точку равновесия, около которой они колеблются (на графиках обозначена пунктирной линией).

1.1.2 Параметры гармонические колебания

Гармонические колебания имеют следующие параметры:

амплитуда (A) — наибольшее отклонение колеблющегося тела от положения равновесия;
период (T) — длительность одного цикла (например, в секундах)

tibble(t = seq(0, 7*pi, by = 0.001),
       y = cos(t)) %>% 
  ggplot(aes(t, y))+
  annotate("rect", xmin = 0, xmax = 2*pi, ymin = -1, ymax = 1, alpha = 0.5, fill = "lightblue")+
    geom_line()+
  geom_hline(yintercept = 0, linetype = 2)+
  annotate("segment", x = 0.3, xend = 6, y = 1, yend = 1, color = "darkgreen", size = 2, arrow = arrow(ends = "both"))+
  annotate("text", x = 3.2, y = 0.85, label = "T", size = 8, color = "darkgreen")+
  annotate("segment", x = 4*pi, xend = 4*pi, y = 0, yend = 1, color = "firebrick3", size = 2, arrow = arrow(ends = "both")) +
  annotate("text", x = 4*pi+0.6, y = 0.5, label = "A", size = 8, color = "firebrick3") +
  annotate("segment", x = 5*pi, xend = 5*pi, y = 0, yend = -1, color = "firebrick3", size = 2, arrow = arrow(ends = "both")) +
  annotate("text", x = 5*pi+0.6, y = -0.4, label = "A", size = 8, color = "firebrick3")+
  labs(caption = "cos(x)")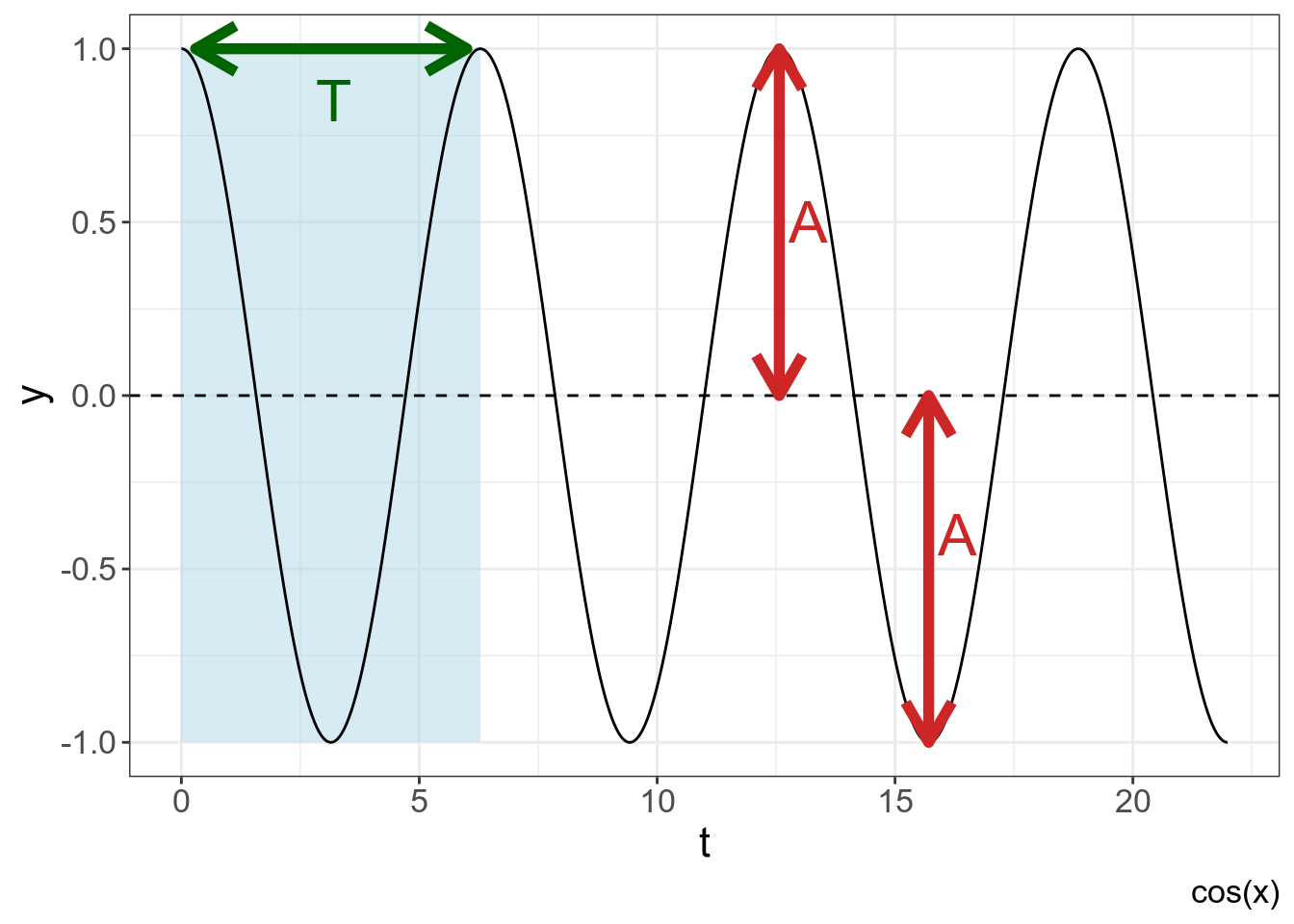

частота (f) — число периодов за секунду

\[f = \frac{1}{T}; T = \frac{1}{f}\]

Звуковая волна — обычная гармоническое колебания, а параметры этого колебания связаны с некоторыми параметрами нашего восприятия:

мы воспринимаем изменения в частотах как изменения в “высоте” звука;
мы воспринимаем изменения в амплитуде волны как изменения в “громкости” звука.
фаза (φ) — цикл гармонического колебания можно разделить на 360°

Вот так это выглядит в декартовой системе координат:

tibble(t = seq(0, 2*pi, by = 0.001),
       y = sin(t)) %>% 
  ggplot(aes(t, y))+
  geom_line()+
  geom_hline(yintercept = 0, linetype = 2)+
  annotate("point", x = 2*pi/4*0:4, y = 0)+
  annotate("text", x = 2*pi/4*0:4, label = paste0(90*0:4, "°"), y = -0.05, size = 4)+
  labs(caption = "sin(x)")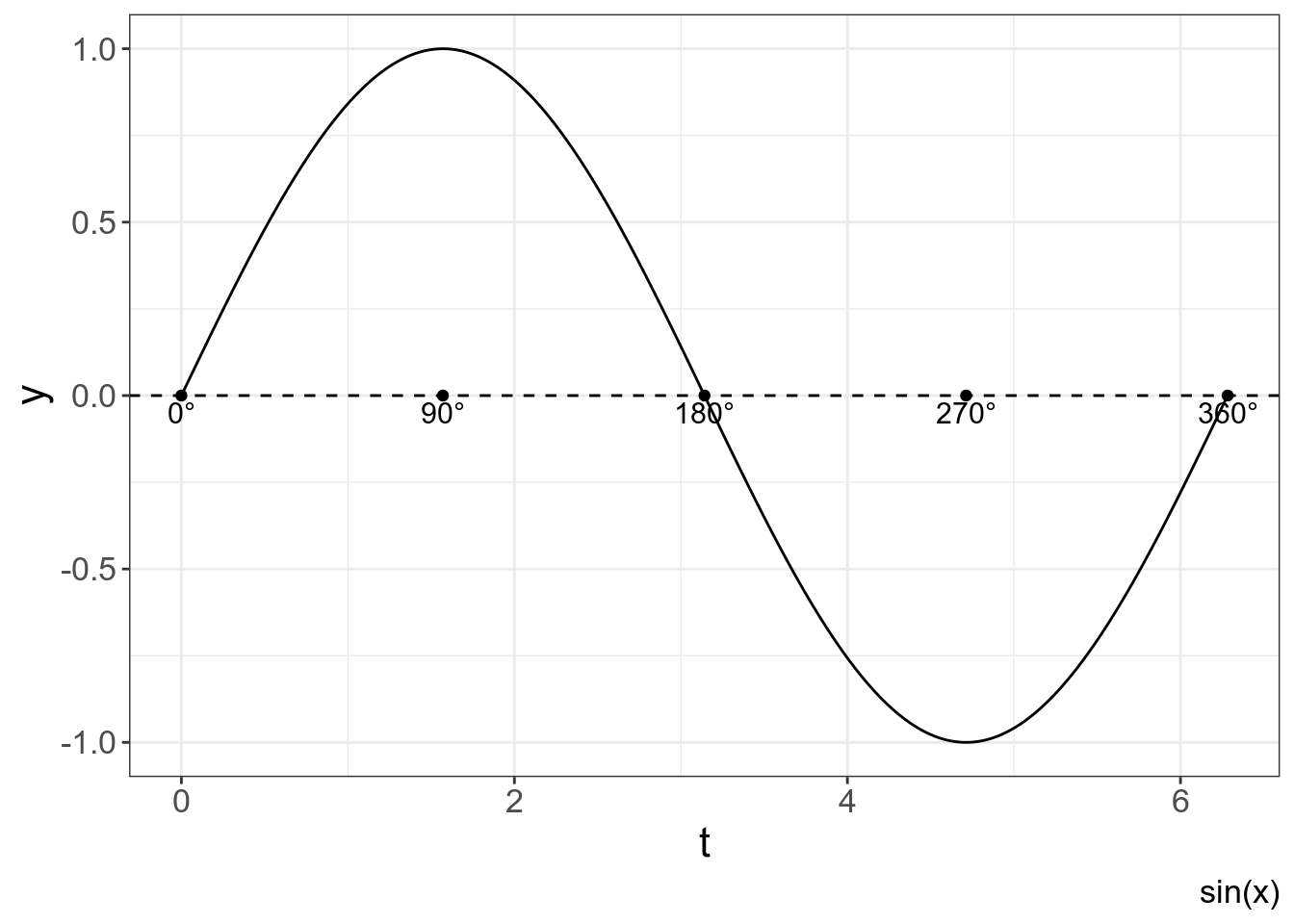

Вот так это выглядит в полярной системе координат:

tibble(t = seq(0, 2*pi, by = 0.001),
       y = sin(t)) %>% 
  ggplot(aes(t, y))+
  geom_line()+
  geom_hline(yintercept = 0, linetype = 2)+
  annotate("point", x = 2*pi/4*1:4, y = 0)+
  annotate("text", x = 2*pi/4*1:4, label = paste0(90*1:4, "°"), y = 0.2, size = 4)+
  coord_polar(start = -pi/2, direction = -1)+
  labs(caption = "sin(x)")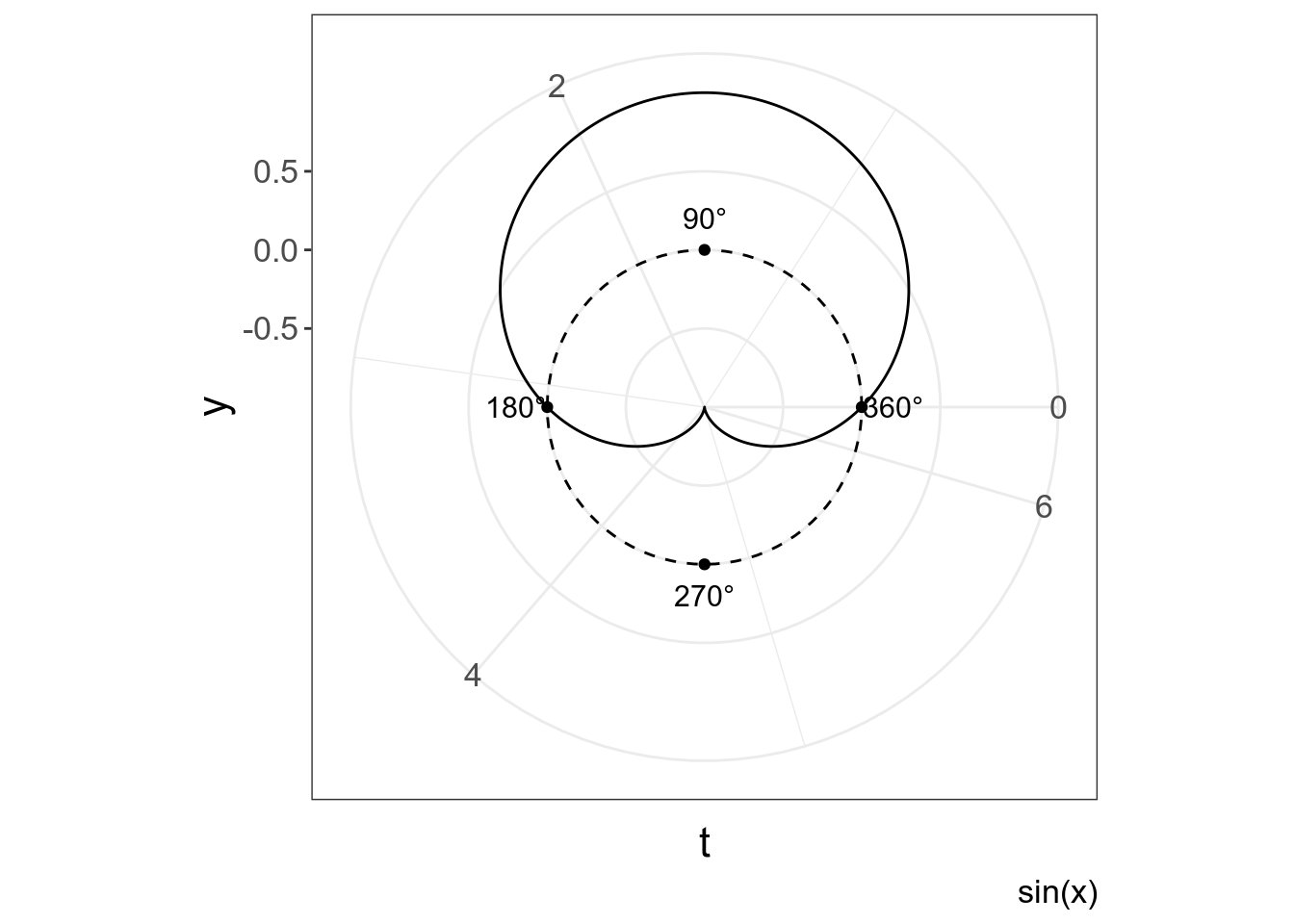

Вот пример другой волны:

tibble(t = seq(0, 2*pi, by = 0.001),
       y = sin(t)+sin(2*t)) %>% 
  ggplot(aes(t, y))+
  geom_line()+
  geom_hline(yintercept = 0, linetype = 2)+
  annotate("point", x = 2*pi/4*0:4, y = 0)+
  annotate("text", x = 2*pi/4*0:4, label = paste0(90*0:4, "°"), y = c(-0.2, -0.2, -0.4, 0.2, 0.2), size = 4) ->
  p1

tibble(t = seq(0, 2*pi, by = 0.001),
       y = sin(t)+sin(2*t)) %>% 
  ggplot(aes(t, y))+
  geom_line()+
  geom_hline(yintercept = 0, linetype = 2)+
  annotate("point", x = 2*pi/4*1:4, y = 0)+
  annotate("text", x = 2*pi/4*1:4, label = paste0(90*1:4, "°"), y = 0.55, size = 4)+
  coord_polar(start = -pi/2, direction = -1)+
  labs(caption = "sin(x)+sin(2x)") ->
  p2
gridExtra::grid.arrange(p1, p2, nrow = 1)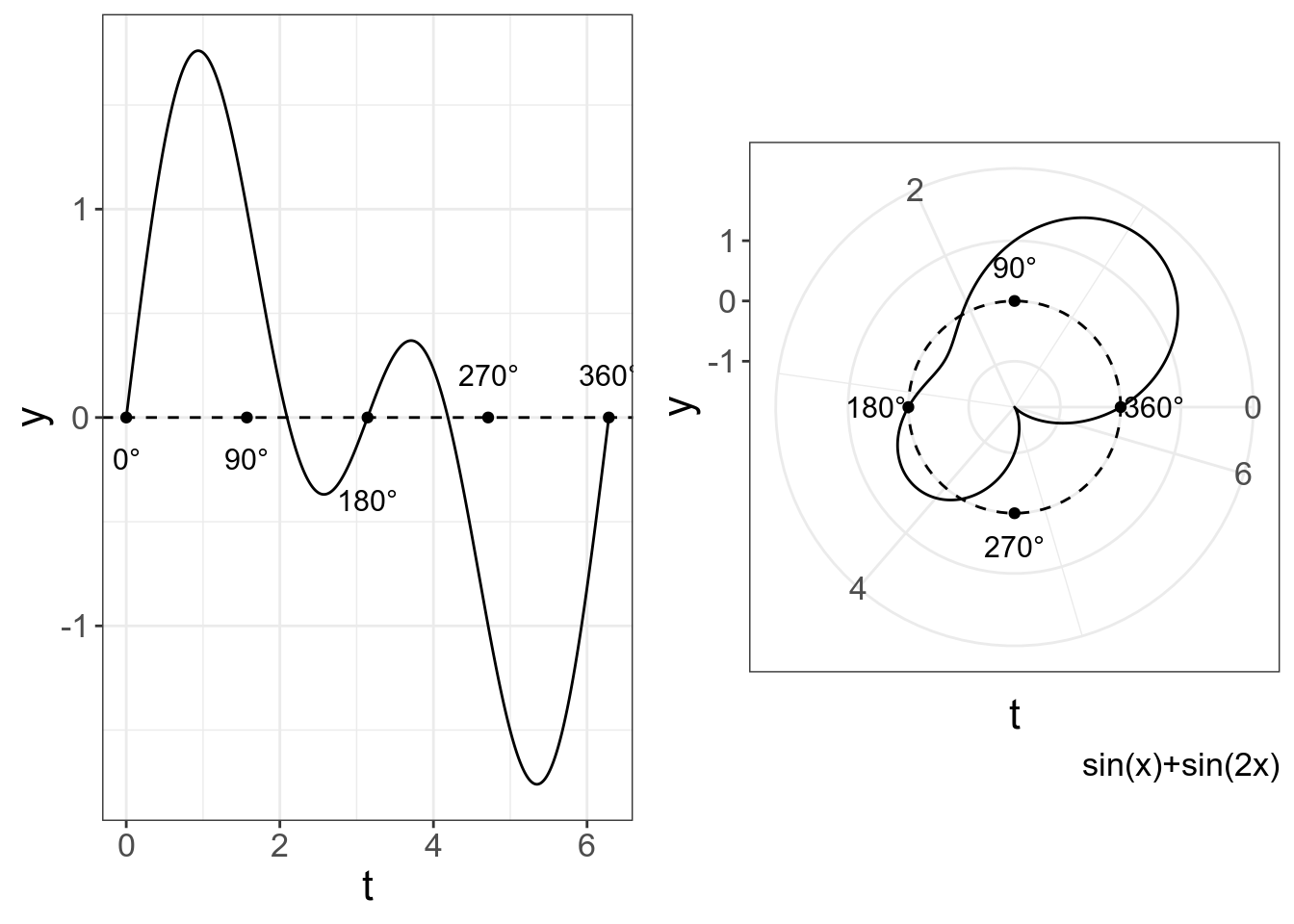

А теперь можно убедиться, что косинус и синус это одно и то же, и различаются лишь фазой:

tibble(t = seq(0, 2*pi, by = 0.001),
       sin = sin(t),
       cos = cos(t)) %>% 
  gather(type, y, sin:cos) %>% 
  ggplot(aes(t, y, color = type))+
  geom_line(show.legend = FALSE)+
  geom_hline(yintercept = 0, linetype = 2)+
  annotate("point", x = 2*pi/4*0:4, y = 0)+
  annotate("text", x = 2*pi/4*0:4, label = paste0(90*0:4, "°"), y = -0.1, size = 4) ->
  p3 

tibble(t = seq(0, 2*pi, by = 0.001),
       sin = sin(t),
       cos = cos(t)) %>% 
  gather(type, y, sin:cos) %>% 
  ggplot(aes(t, y, color = type))+
  geom_line()+
  geom_hline(yintercept = 0, linetype = 2)+
  annotate("point", x = 2*pi/4*1:4, y = 0)+
    annotate("text", x = 2*pi/4*1:4, label = paste0(90*1:4, "°"), y = 0.55, size = 4)+
  coord_polar(start = -pi/2, direction = -1) +
  theme(legend.position = "top")->
  p4
gridExtra::grid.arrange(p3, p4, nrow = 1)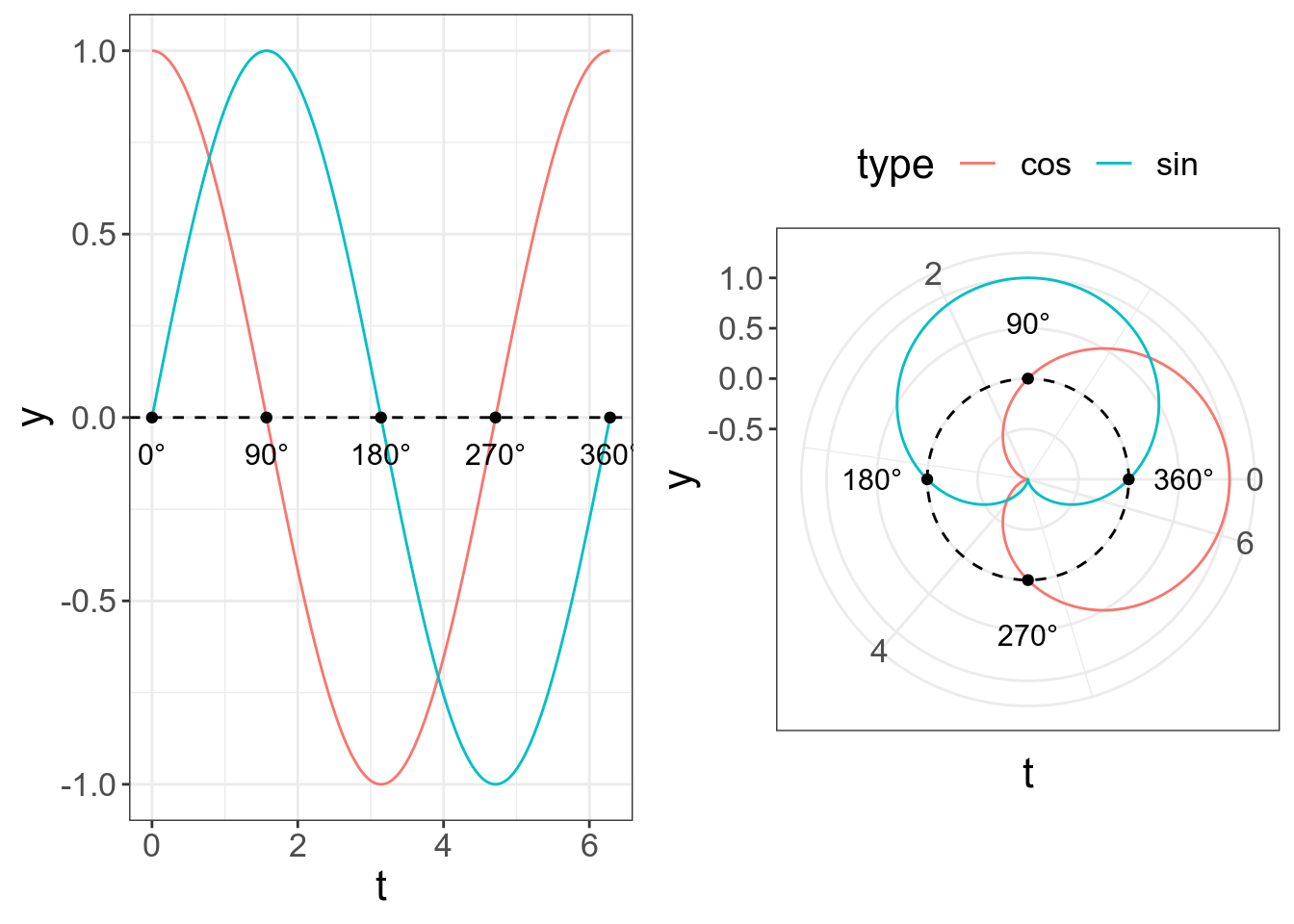

Теперь мы можем определить гармонические калебания следующей формулой:

\[s(t) = A \times \cos(2\pi ft+\phi)\]

A — амплитуда
f — частота колебания
\(\phi\) — фаза
t — время

1.1.3 Сложение волн

Если сложить две одинаковые волны, получится волна с такой же частотой и фазой, а их совместная амплитуды, сложившись друг с другом, удвоится:

tibble(t = seq(0, 9*pi, by = 0.001),
      `wave 1` = sin(t),
      `wave 2` = sin(t),
      `wave 1 + wave 2` = `wave 1`  + `wave 2`) %>% 
  gather(type, y, `wave 1`:`wave 1 + wave 2`) %>% 
  mutate(type = factor(type, levels = c("wave 1", "wave 2", "wave 1 + wave 2"))) %>% 
  ggplot(aes(t, y))+
  geom_line()+
  geom_hline(yintercept = 0, linetype = 2)+
  facet_wrap(~type, nrow = 3)+
  labs(caption = "wave 1 = wave 2 = sin(x)")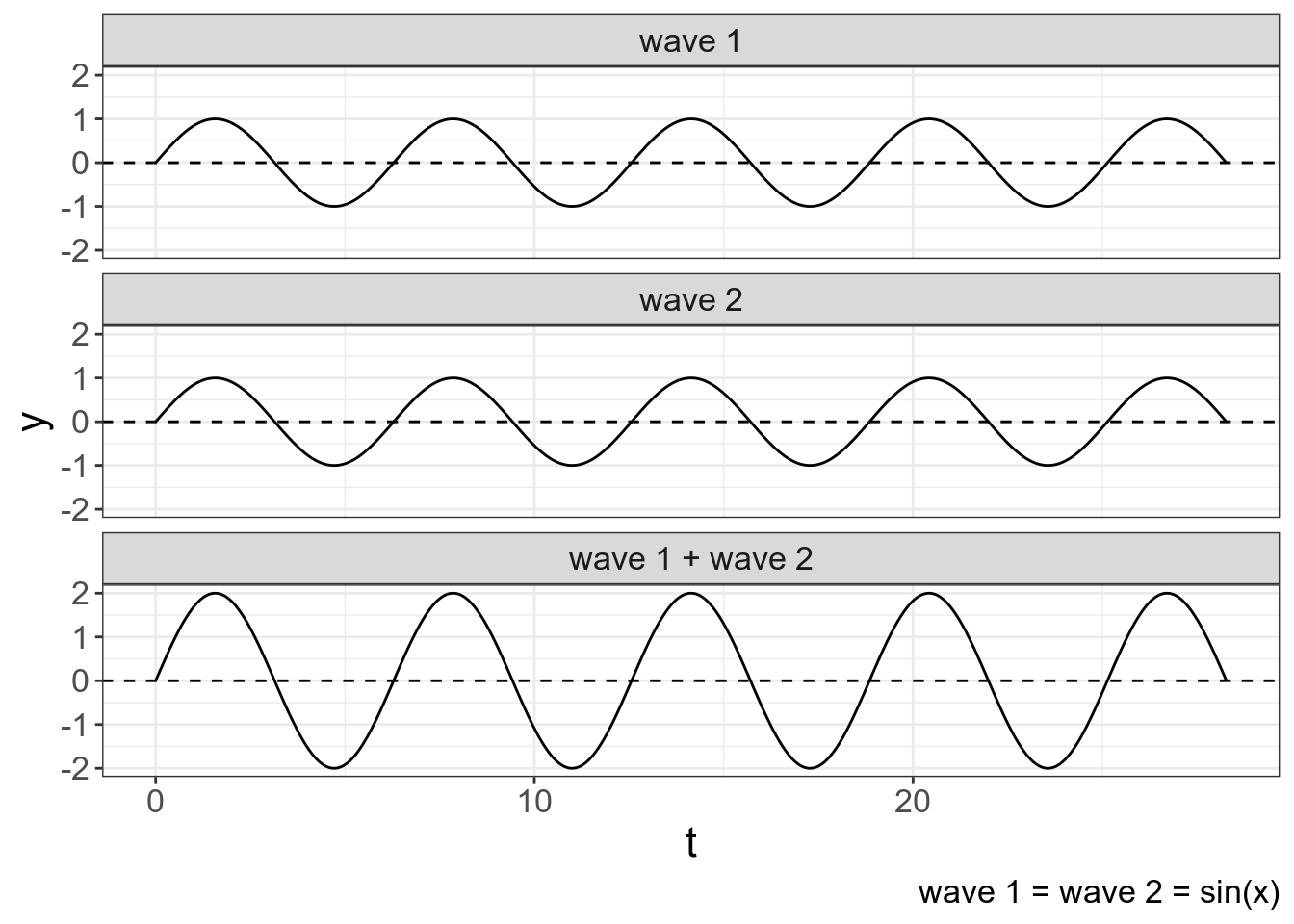

Если две одинаковые волны находятся в полной противофазе, то они нейтрализуют амплитуды друг друга:

tibble(t = seq(0, 9*pi, by = 0.001),
      `wave 1` = sin(t),
      `wave 2` = sin(t-pi),
      `wave 1 + wave 2` = `wave 1` + `wave 2`) %>% 
  gather(type, y, `wave 1`:`wave 1 + wave 2`) %>% 
  mutate(type = factor(type, levels = c("wave 1", "wave 2", "wave 1 + wave 2"))) %>% 
  ggplot(aes(t, y))+
  geom_line()+
  geom_hline(yintercept = 0, linetype = 2)+
  facet_wrap(~type, nrow = 3)+
  labs(caption = "wave 1 = sin(x), wave 2 = sin(t-pi)")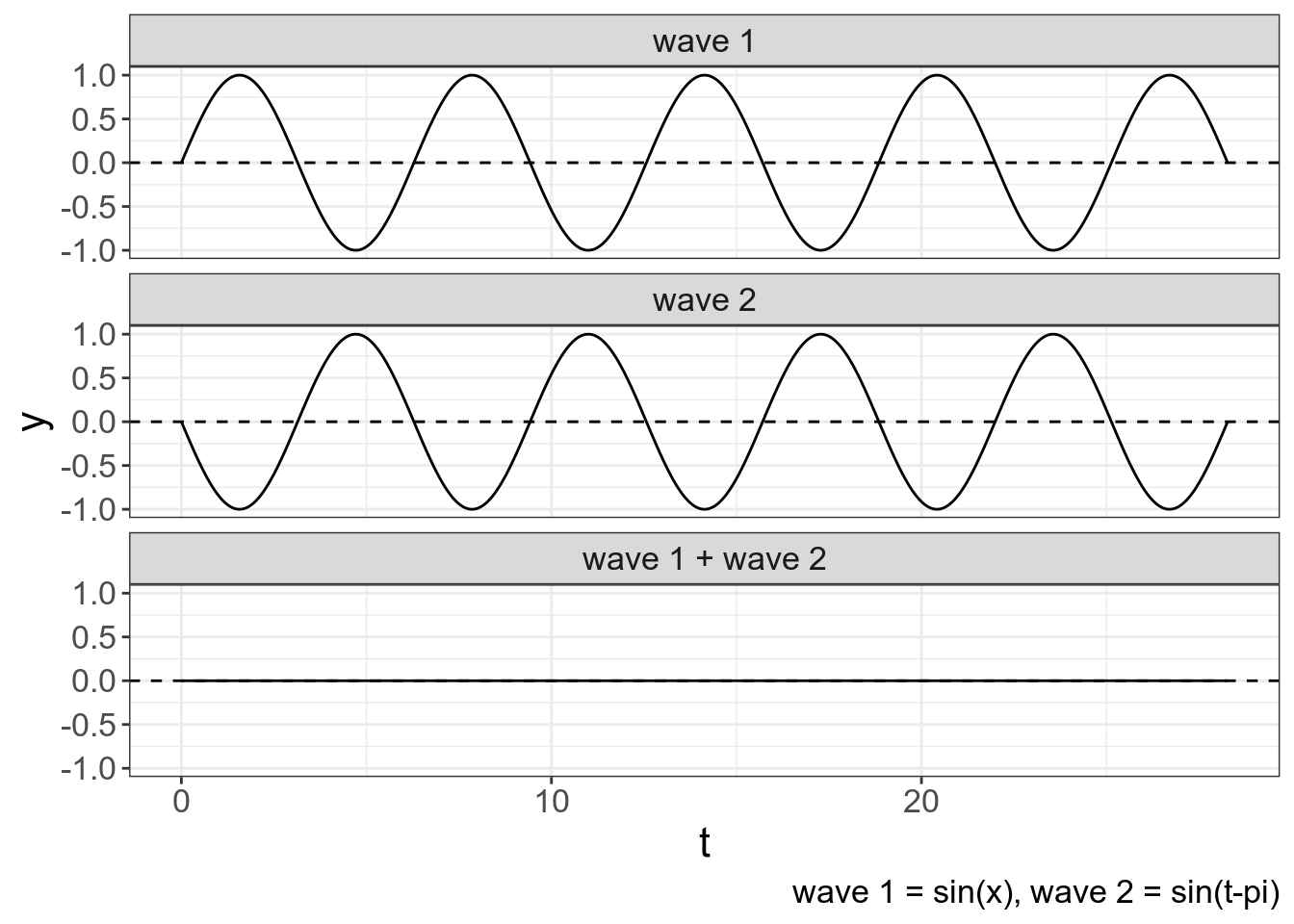

В остальном, сложение волн можно представить, как поточечное сложение каждых элементов волны:

tibble(t = seq(0, 9*pi, by = 0.001),
      `wave 1` = sin(t),
      `wave 2` = sin(2*t),
      `wave 1 + wave 2` = `wave 1` + `wave 2`) %>% 
  gather(type, y, `wave 1`:`wave 1 + wave 2`) %>% 
  mutate(type = factor(type, levels = c("wave 1", "wave 2", "wave 1 + wave 2"))) %>% 
  ggplot(aes(t, y))+
  geom_line()+
  geom_hline(yintercept = 0, linetype = 2)+
  facet_wrap(~type, nrow = 3)+
  labs(caption = "wave 1 = sin(x), wave 2 = sin(2t)")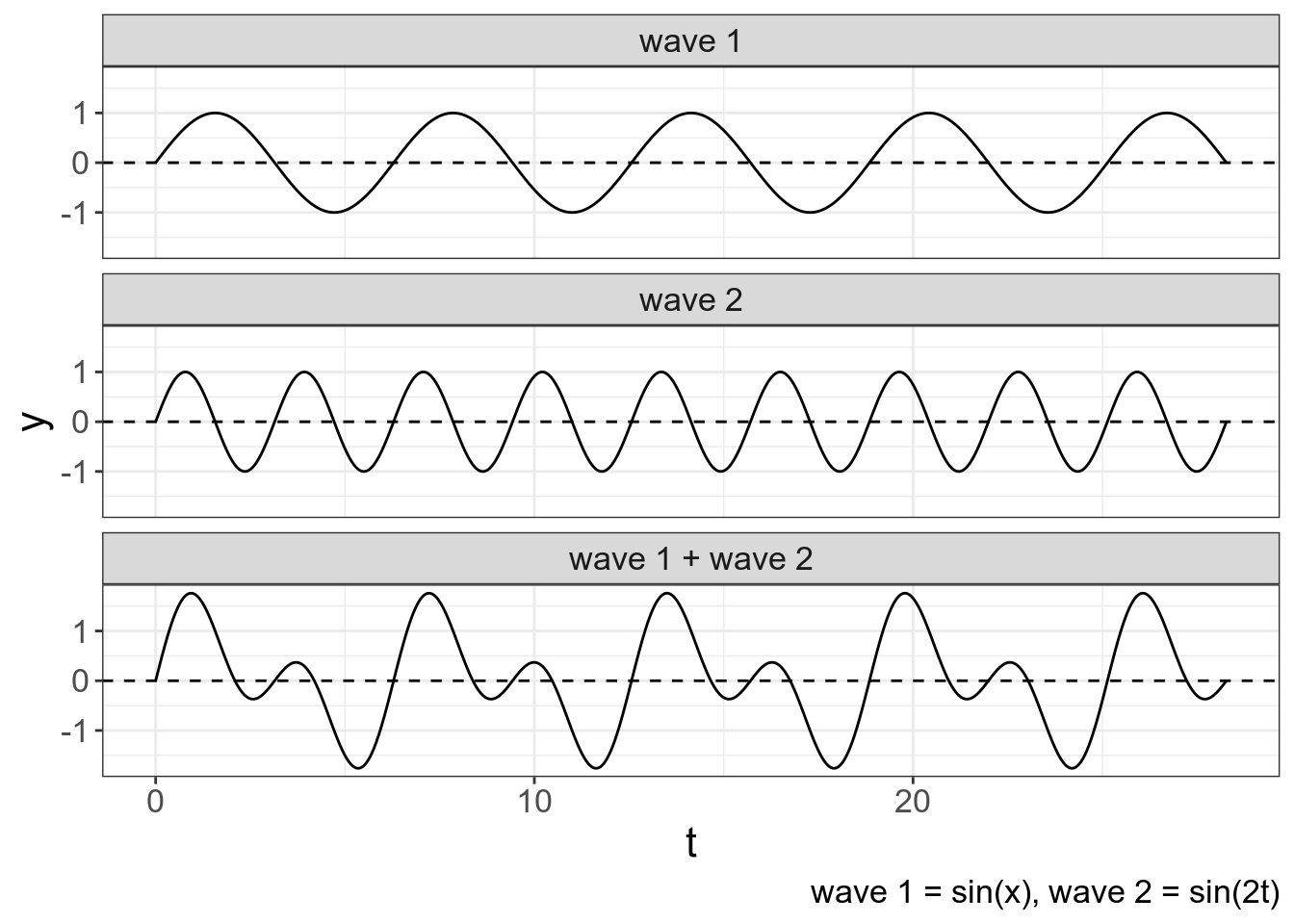

“Биение” — явление изменения амплитуды суммы двух волн с несильной разницей в частоте.

tibble(t = seq(0, 2*pi, by = 0.001),
      `198 Hz` = sin(198*t),
      `200 Hz` = sin(200*t),
      `198 Hz + 200 Hz` = `198 Hz` + `200 Hz`) %>% 
  gather(type, y, `198 Hz`:`198 Hz + 200 Hz`) %>% 
  mutate(type = factor(type, levels = c("198 Hz", "200 Hz", "198 Hz + 200 Hz"))) %>% 
  ggplot(aes(t, y))+
  geom_line()+
  geom_hline(yintercept = 0, linetype = 2)+
  facet_wrap(~type, nrow = 3)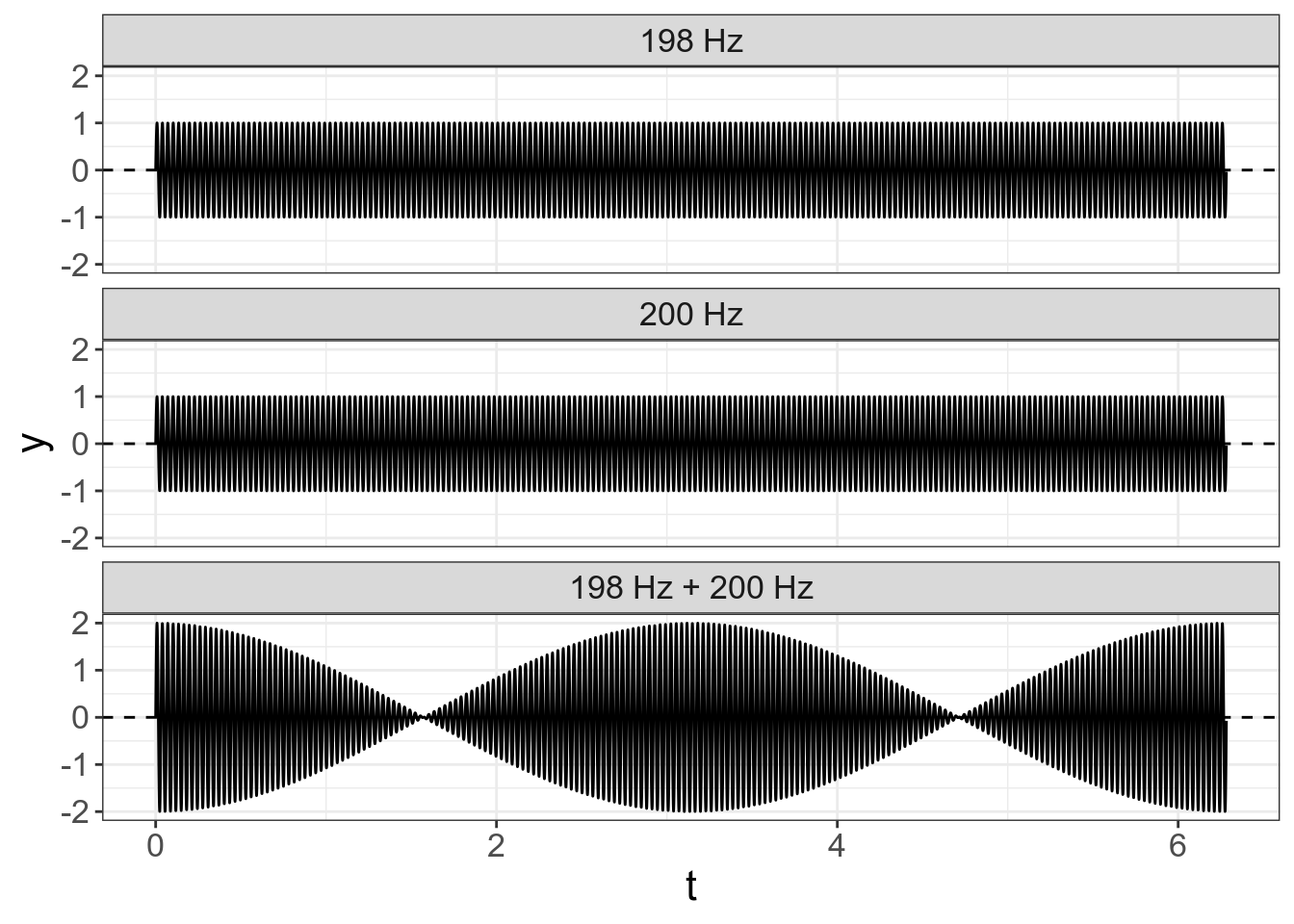

198 Hz

200 Hz

198 Hz + 200 Hz

1.2 Комплексные числа и формула Эйлера

1.2.1 Комплексные числа

На рубеже XVIII-XIX веков К. Ф. Гаусс доказад формулу о том, что каждый многочлен, степень которого не меньше единицы, имеет хотя бы один действительный или комлексный корень. Эта формула использует комлексные числа, придуманные впервые в XVI веке (впервые квадрытные корни из отрицательных числе появляются у математика Дж. Кордано).

Комплексные числа называют упорядоченные пары действительных чисел, второй из которых записывают, используя символ \(i\), (а иногда \(j\)) например, \(5 + 6i\), \(2 - i\), \(9 + 0i\). (обычно второе слогаемое в таком случае опускают) Все арифметические действия с комлексными числами осуществляется по обычным правилам с учетом равенства \(i^2 = -1\). Комплексное число состоит из двух частей:

действительной \(Re(5+6i) = 5\)
мнимой \(Im(5+6i) = 6\)

Модулем или абсолютныой величеной комплексного числа \(z = a - ib\) называют число \(|z| = \sqrt{a^2+b^2}\).

Комплексные числа также можно изобразить в виде вектора на координатной плоскости, отложив по оси абсцисс действительную часть, а по оси ординат мнимую часть:

tibble(z = c(0+0i, 4+3i)) %>% 
  ggplot(aes(Re(z), Im(z)))+
  geom_path(arrow = arrow())+
  annotate("text", x = 2, y = 1.8, label = "z", size = 8)+
  scale_y_continuous(breaks = 0:3, labels = paste0(0:3, "𝒾 "))+
  labs(caption = "z = 4+3𝒾 ")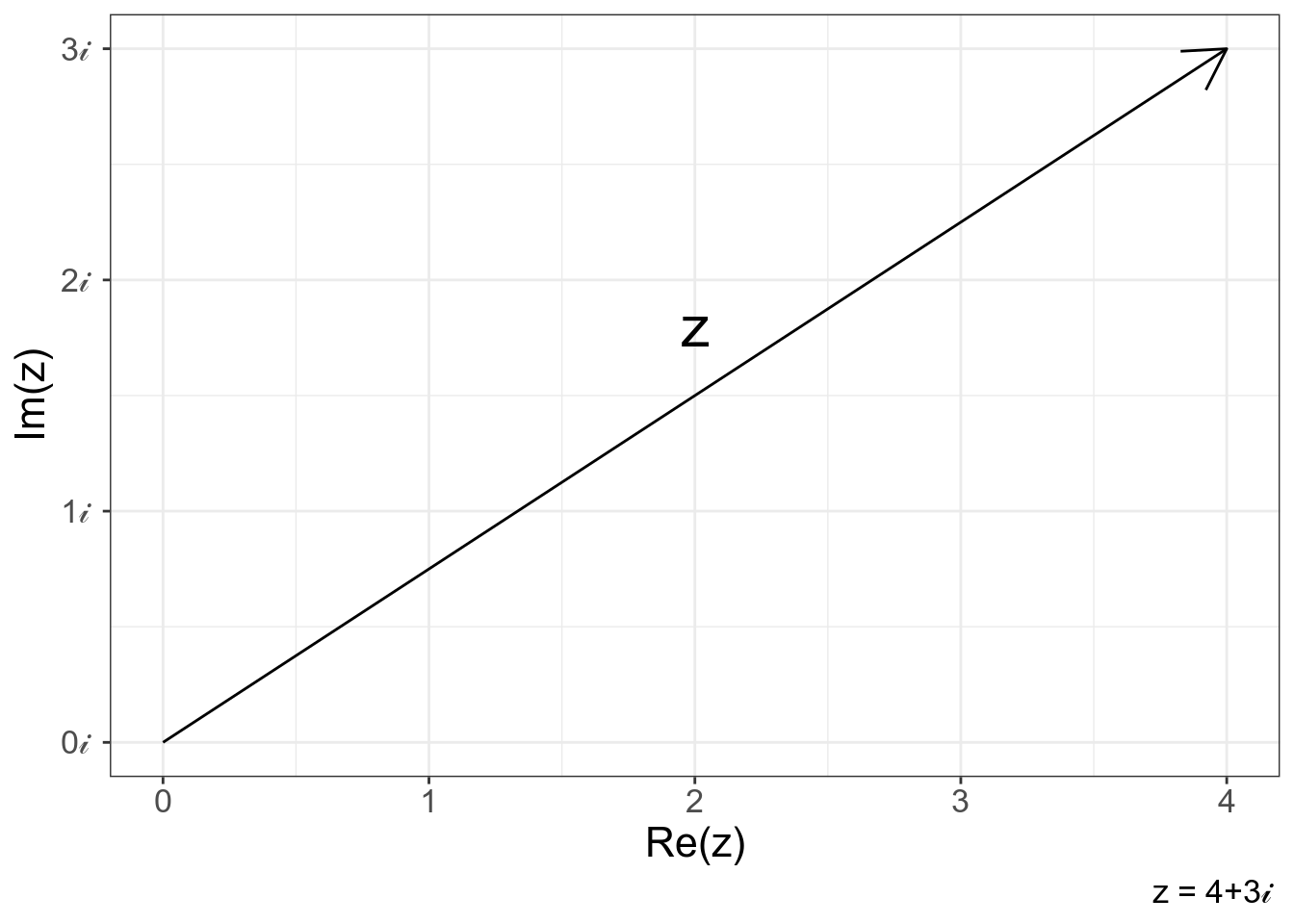

🤔 Назовите модуль числа z на предыдущем графике.

В результате сложения двух комлексных чисел \(z_1 = x_1 + y_1i\) и \(z_2 = x_2 + y_2i\) получается комлпесное число \(z_3 = x_3 + y_3i\), где

\(x_3 = x_1 + x_2\)
\(y_3 = y_1 + y_2\)

tibble(z = c(0 + 0i, 3+1i, 0 + 0i, 1+3i, 0 + 0i, 4+4i),
       x = c("z1", "z1", "z2", "z2", "z3", "z3"),
       clr = c("1", "1", "1", "1", "2", "2")) %>% 
  ggplot(aes(Re(z), Im(z), group = x, color = clr))+
  geom_line(arrow = arrow(), show.legend = FALSE)+
  annotate("segment", x = Re(3+1i), y = Im(3+1i), xend = Re(4+4i), yend = Im(4+4i), linetype = 2)+
  annotate("segment", x = Re(1+3i), y = Im(1+3i), xend = Re(4+4i), yend = Im(4+4i), linetype = 2)+
  annotate("text", x = 0.4, y = 1.6, label = "z1", size = 8)+
  annotate("text", x = 1.8, y = 0.8, label = "z2", size = 8)+
  annotate("text", x = 1.8, y = 2.2, label = "z3", size = 8)+
  scale_y_continuous(breaks = 0:4, labels = paste0(0:4, "𝒾 "))+
  labs(caption = "z3 = z1 + z2")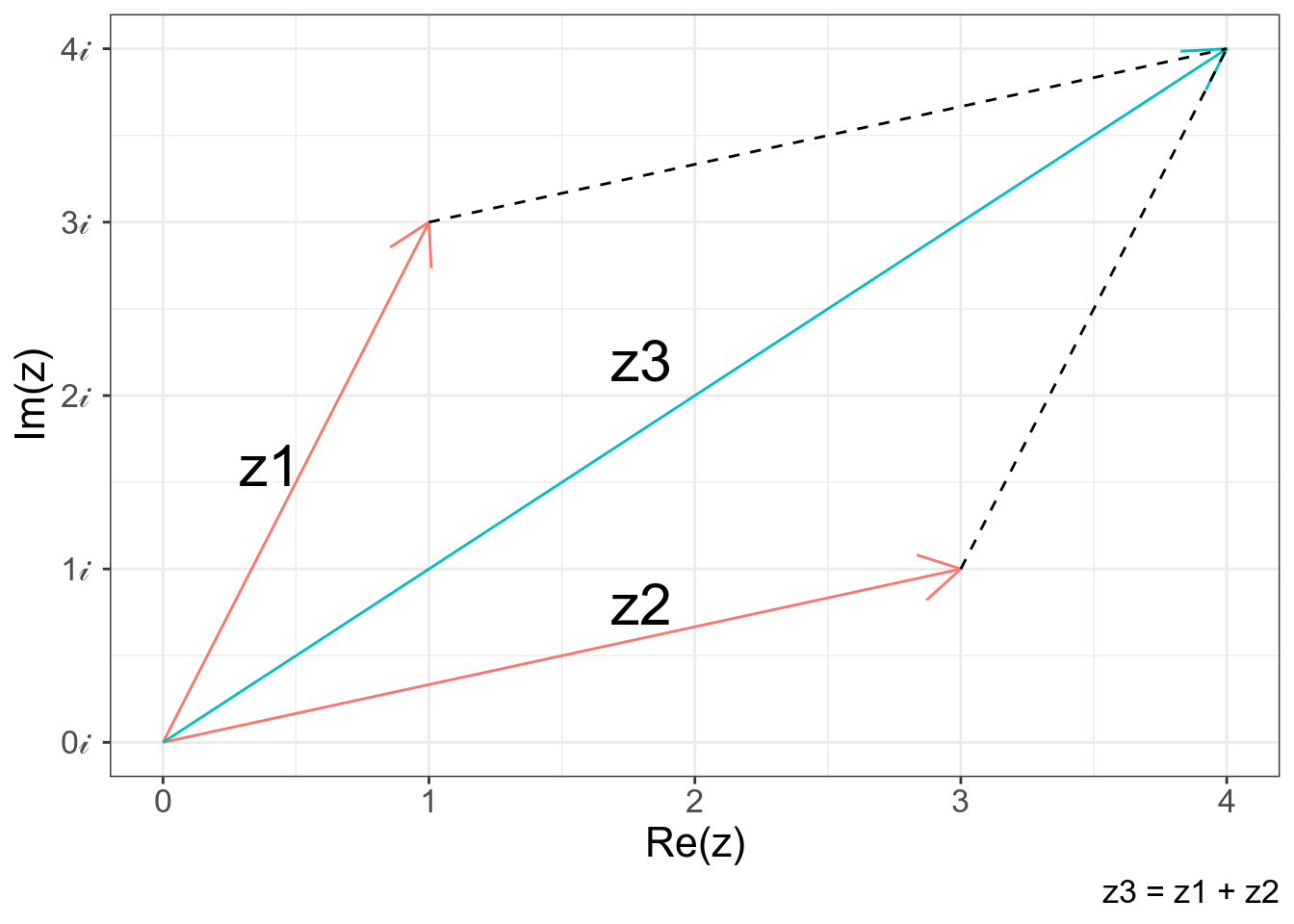

Комплексное число можно выразить также при помощи тригонометрических функций:

tibble(z = c(0+0i, 4+3i)) %>% 
  ggplot(aes(Re(z), Im(z)))+
  geom_path(arrow = arrow(), size = 2)+
  annotate("text", x = 2, y = 1.8, label = "r", size = 8)+
  annotate("segment", x = 0, y = 0.2, xend = 3.8, yend = 3, arrow = arrow(ends = "both", type = "closed"), linetype = 2)+
  annotate("curve", x = 0.5, y = 0, xend = 0.25, yend = 0.2)+
  annotate("text", x = 0.55, y = 0.2, label = "θ", size = 8)+
  annotate("segment", x = 0.1, y = 0, xend = 4, yend = 0, arrow = arrow(ends = "both", type = "closed"), linetype = 2)+
  annotate("segment", x = 0.1, y = 0, xend = 4, yend = 0, arrow = arrow(ends = "both", type = "closed"), linetype = 2)+
  annotate("text", x = 2, y = 0.15, label = "x", size = 8)+
  annotate("segment", x = 4, y = 0.05, xend = 4, yend = 2.9, arrow = arrow(ends = "both", type = "closed"), linetype = 2)+
  annotate("text", x = 3.85, y = 1.5, label = "y", size = 8)+
  scale_y_continuous(breaks = 0:3, labels = paste0(0:3, "𝒾 "))+
  labs(caption = "z = x + y𝒾 = 4 + 3𝒾 ")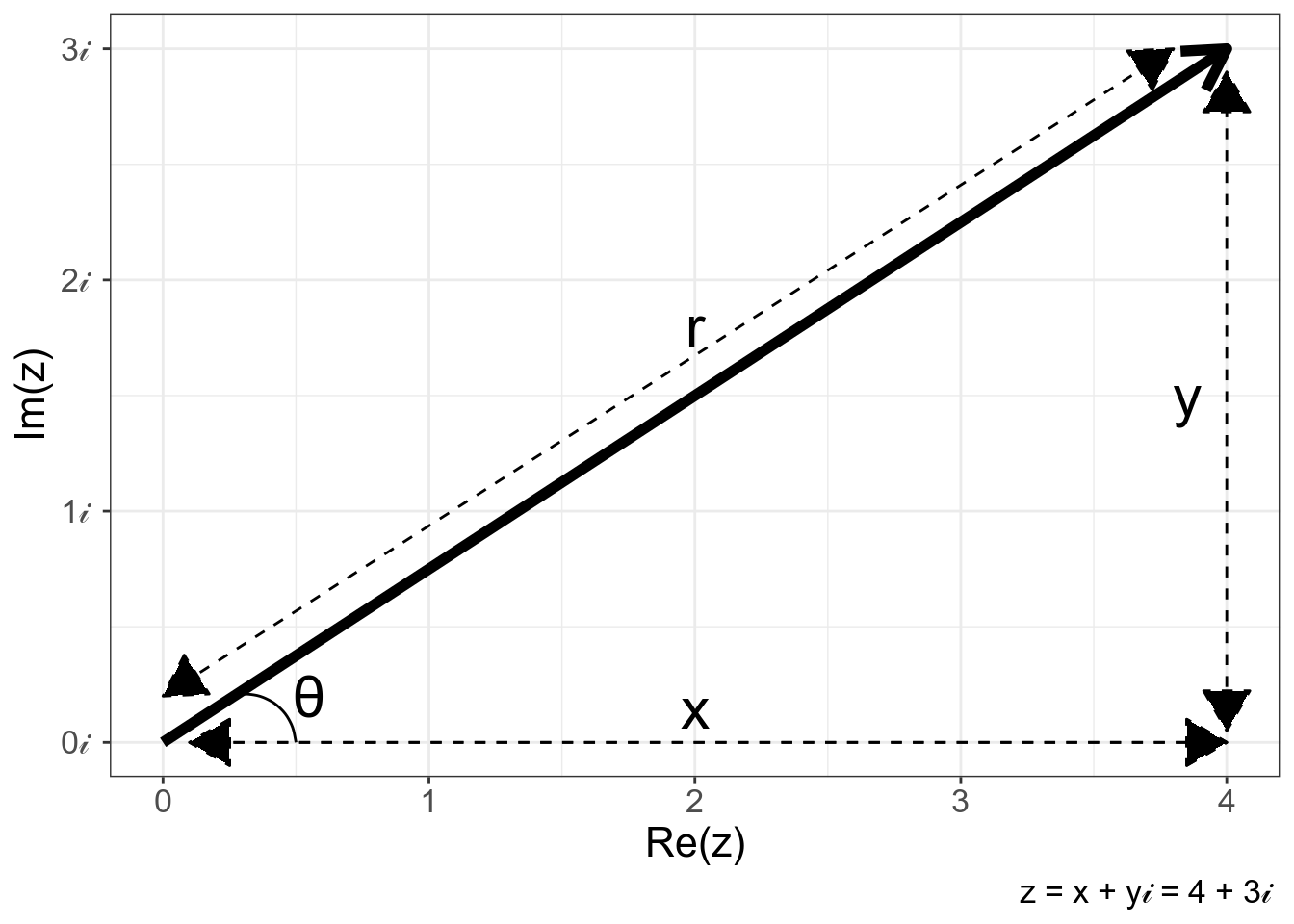

модуль: \(|z| = r = \sqrt{(r\times \cos(θ))^2+ (r\times \sin(θ))^2} = r \sqrt{\cos(θ)^2+ \sin(θ)^2}\)
действительная часть: \(x = r\times \cos(θ)\)
мнимая часть: \(y = r\times \sin(θ)\)
комплексное число: \(z = r\times \cos(θ) + 𝒾 r\times \sin(θ)\)

Таким образом волны можно считать действительной частью некоторых мнимых чисел

\[s(t) = A \times \cos(2\pi ft+\phi) = Re(z)\]

1.2.2 Формула Эйлера

Гармонические колебания тесно связаны с комплексными экспоненциальными функциями, благодаря формуле Эйлера:

\[e^{ix}=\cos(x)+i\sin(x),\] где x — действительное число.

Таким образом любое мнимое число может быть записано в виде:

\[z = r\times e^{iθ}\]

Тогда любую волну можно записать следующим образом:

\[ s(t) = Re\left[ A \times e^{i(2\pi ft+\phi)}\right] = A \times Re\left[ e^{i(2\pi ft+\phi)}\right] \]

1.3 Преобразование Фурье

Спектр пытались анализировать давно: многие исследовали радугу, например, Теодор из Фрайбарга обнаружил первичную и вторичную радуги в начале XIV века. Фурье показал, чоказал функция может быть представлена в виде суммы простых переодических функций (например, синусоид).

Давайте посмотрим прекрасное видео Гранта Сандерсона (3blue1brown).

В видео формула преобразования Фурье выглядит вот так:

\[\hat{g}(f) = \int_{-\infty}^{+\infty}g(t)\times e^{-i2\pi ft}dt\]

Если же вам все же не хочется иметь дело с комлексными числами, можно считать два коэффициента:

\[\hat{g}_a(f) = \int_{-\infty}^{+\infty}g(t)\times\cos({2\pi ft})dt\] \[\hat{g}_b(f) = \int_{-\infty}^{+\infty}g(t)\times\sin({2\pi ft})dt; \]

Когда мы работаем с естественным сигналом, нам не доступна функция, а только некоторое подмножество наблюдений, которые с какой-то частотой снимает микрофон. В связи с этим возникает дискретное преобразование Фурье (Discrete Fourier Transform, DFT):

\[\hat{g}_k = \sum_{n = 0}^{N-1}g_n\times e^{-\frac{i2\pi kn}{N}}, \frac{k}{N} \simeq f, n \simeq t\]

Рассмотрим пример синусоиды с амплитудой 1, с частотой сэмплирования 8Hz, т. е. у нас 8 наблюдений:

points <- tibble(t = seq(0, 1.99*pi, by = pi/4), 
                y = sin(t))

tibble(t = seq(0, 2*pi, by = 0.001),
       y = sin(t)) %>% 
  ggplot(aes(t, y))+
  geom_line()+
  geom_point(data = points, size = 3)+
  geom_text(data = points, aes(label = round(y, 3)), size = 3, nudge_x = 0.4, nudge_y = 0.025)+
  geom_hline(yintercept = 0, linetype = 2)+
  labs(caption = "sin(x)")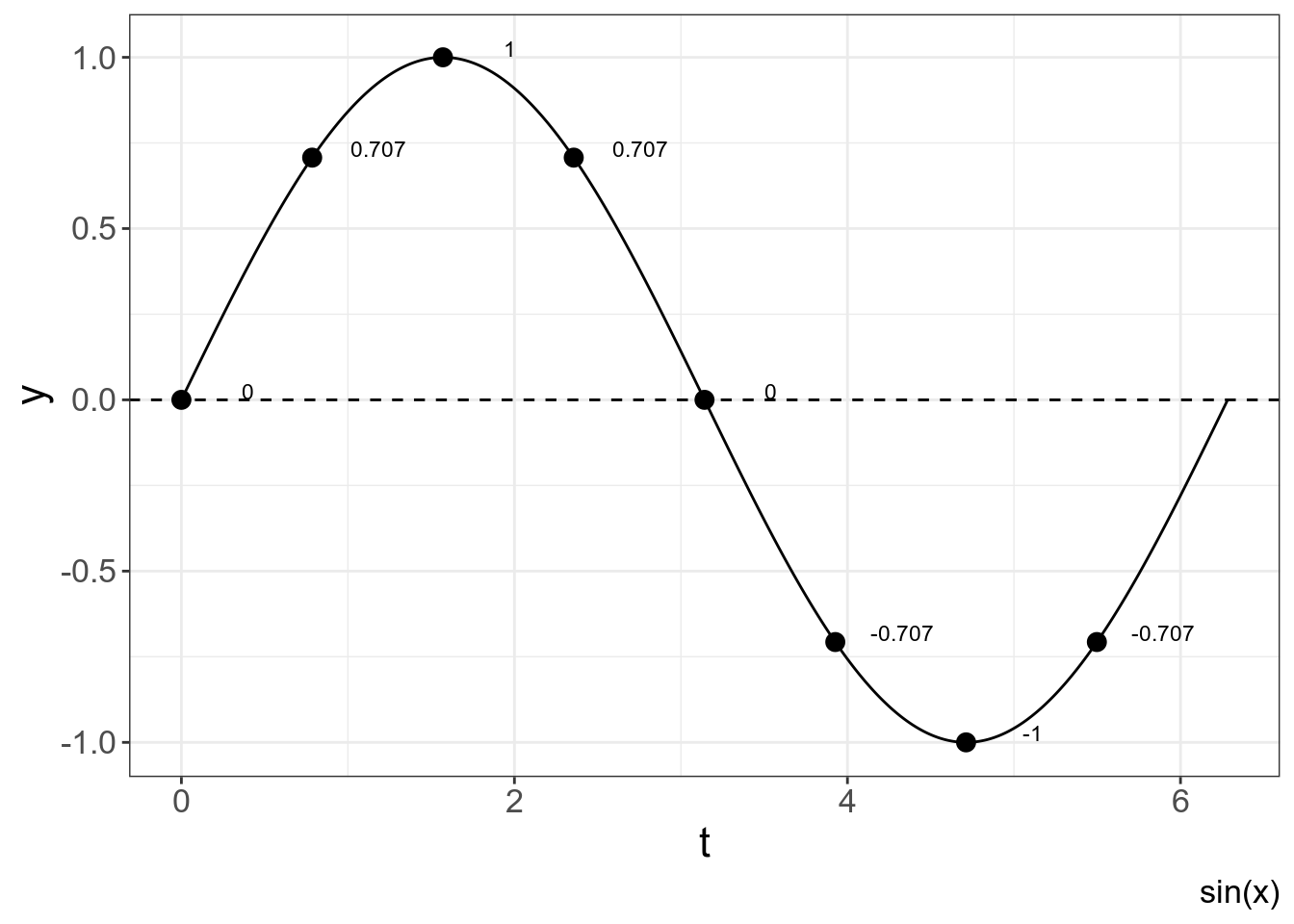

Мы можем посчитать коэфициенты дискретного преобразования Фурье и отметить их на графике:

x <- c(0, 0.707, 1, 0.707, 0, -0.707, -1, -0.707)
n <- 0:7
x_0 <- sum((x*exp(-2i*pi*n*0/length(x))))
x_0

## [1] 0+0i

x_1 <- sum((x*exp(-2i*pi*n*1/length(x))))
x_1

## [1] 0-3.999698i

x_2 <- sum((x*exp(-2i*pi*n*2/length(x))))
x_2

## [1] 1.128e-19+2.449213e-16i

x_3 <- sum((x*exp(-2i*pi*n*3/length(x))))
x_3

## [1] 0+0.0003020228i

x_4 <- sum((x*exp(-2i*pi*n*4/length(x))))
x_4

## [1] 0+2.028015e-16i

x_5 <- sum((x*exp(-2i*pi*n*5/length(x))))
x_5

## [1] 0-0.0003020228i

x_6 <- sum((x*exp(-2i*pi*n*6/length(x))))
x_6

## [1] 2.511757e-15+7.34818e-16i

x_7 <- sum((x*exp(-2i*pi*n*7/length(x))))
x_7

## [1] 0+3.999698i

tibble(f = n,
       coefs = c(x_0, x_1, x_2, x_3, x_4, x_5, x_6, x_7),
       amplitude = abs(coefs)) %>% 
  ggplot(aes(f, amplitude))+
  geom_point()+
  scale_x_continuous(breaks = 0:7, labels = paste(0:7, "Hz"))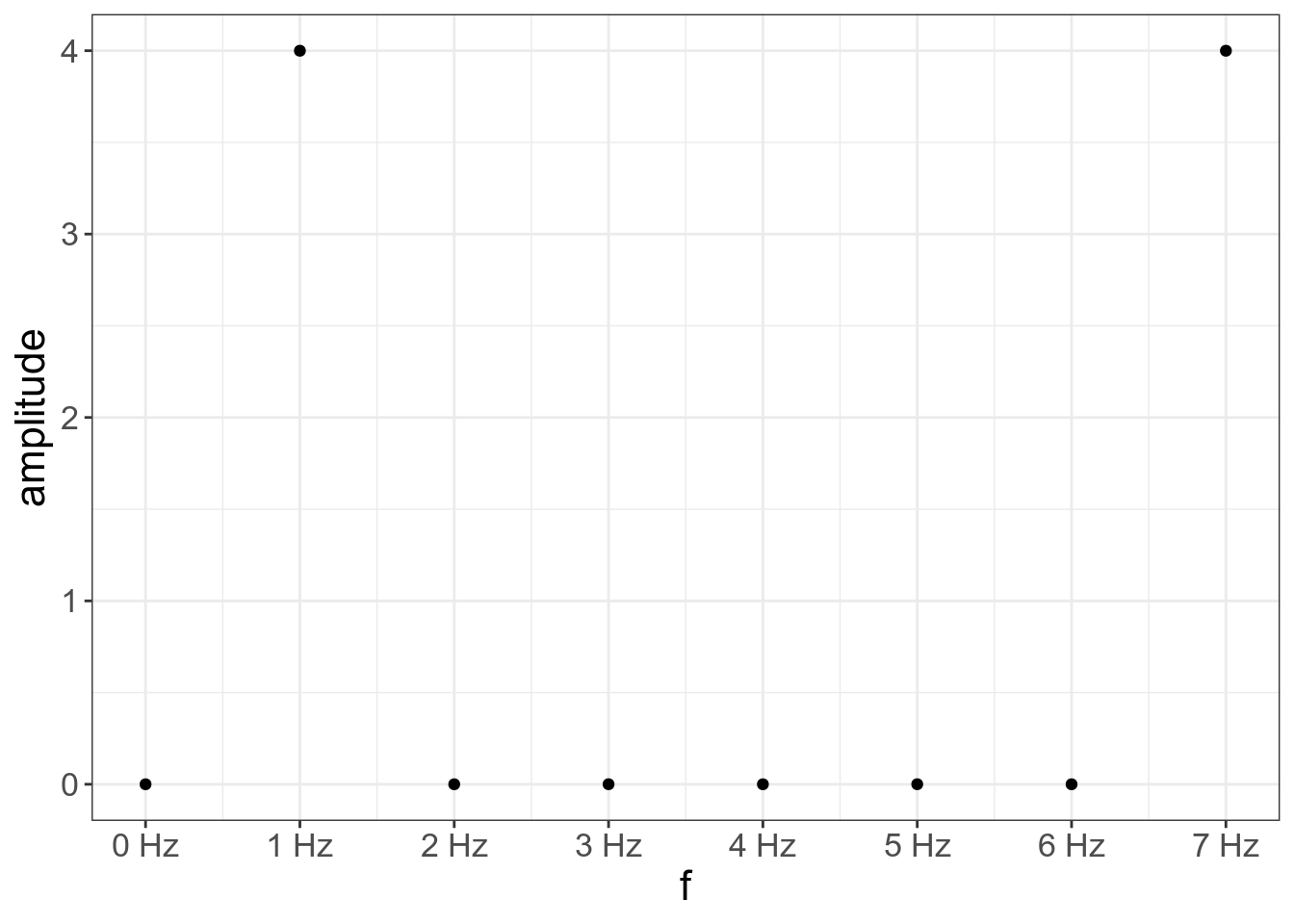

Существует Теорема Котельникова (в англоязычной литературе Найквиста — Шенона), согласно которой чтобы востановить сигнал без потерь частота дискретизации должна быть в два и более раза больше чем самая высокая частота в нашем сигнале. Таким образом мы должны отбросить вторую половину наблюдений, умножив первую на два:

tibble(f = n,
       coefs = c(x_0, x_1, x_2, x_3, x_4, x_5, x_6, x_7)*2,
       amplitude = abs(coefs)) %>% 
  ggplot(aes(f, amplitude))+
  geom_point()+
  xlim(0, length(x)/2-1) # это такой изящный способ получить нужное, не изменяя предыдущий код

## Warning: Removed 4 rows containing missing values (geom_point).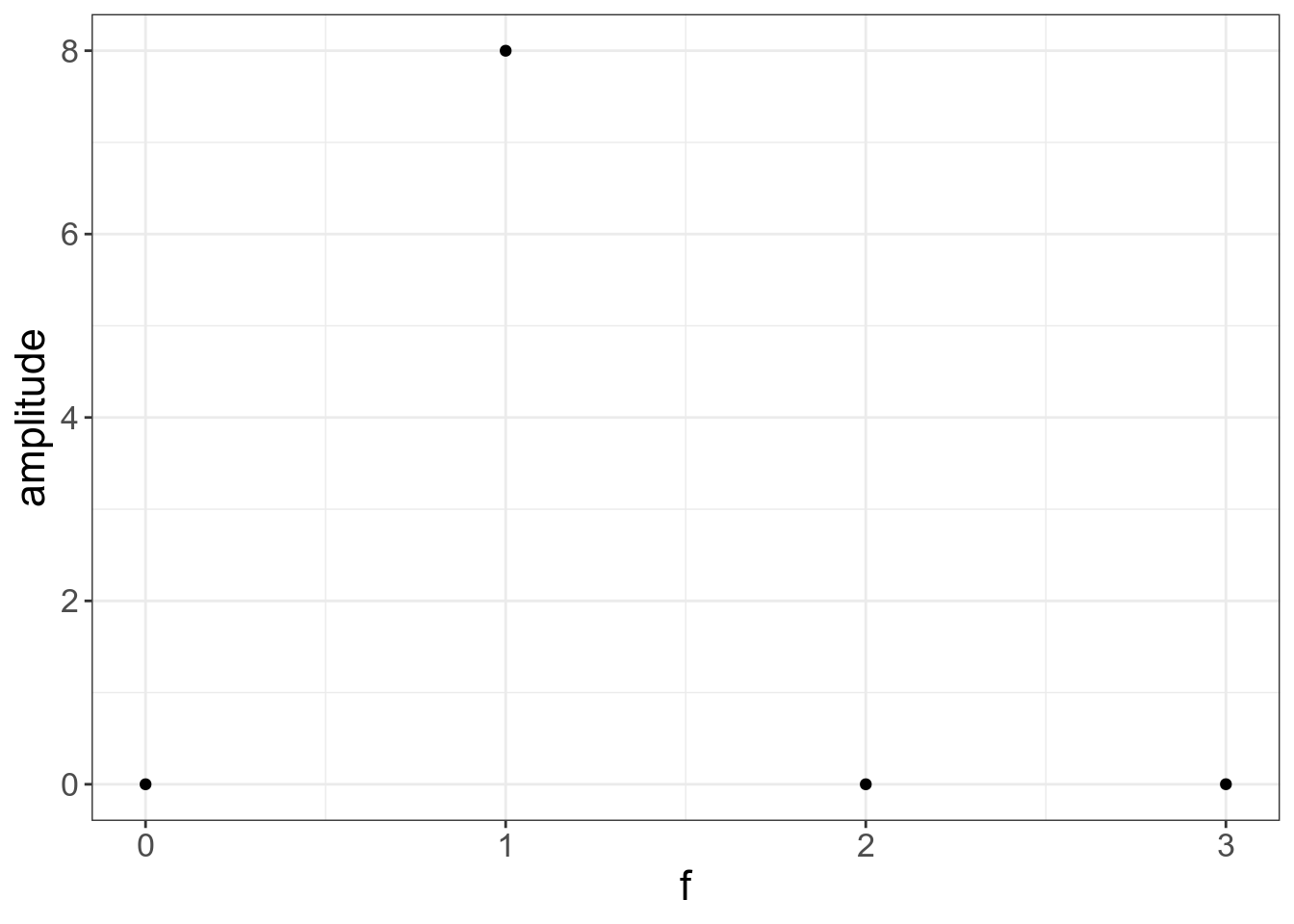

И последний ход: нам нужно разделить полученные амплитуды на 8 наблюдений, которые у нас были:

tibble(f = n,
       coefs = c(x_0, x_1, x_2, x_3, x_4, x_5, x_6, x_7)*2/8,
       amplitude = abs(coefs)) %>% 
  ggplot(aes(f, amplitude))+
  geom_point()+
  xlim(0, length(x)/2-1) # это такой изящный способ получить нужное, не изменяя предыдущий код

## Warning: Removed 4 rows containing missing values (geom_point).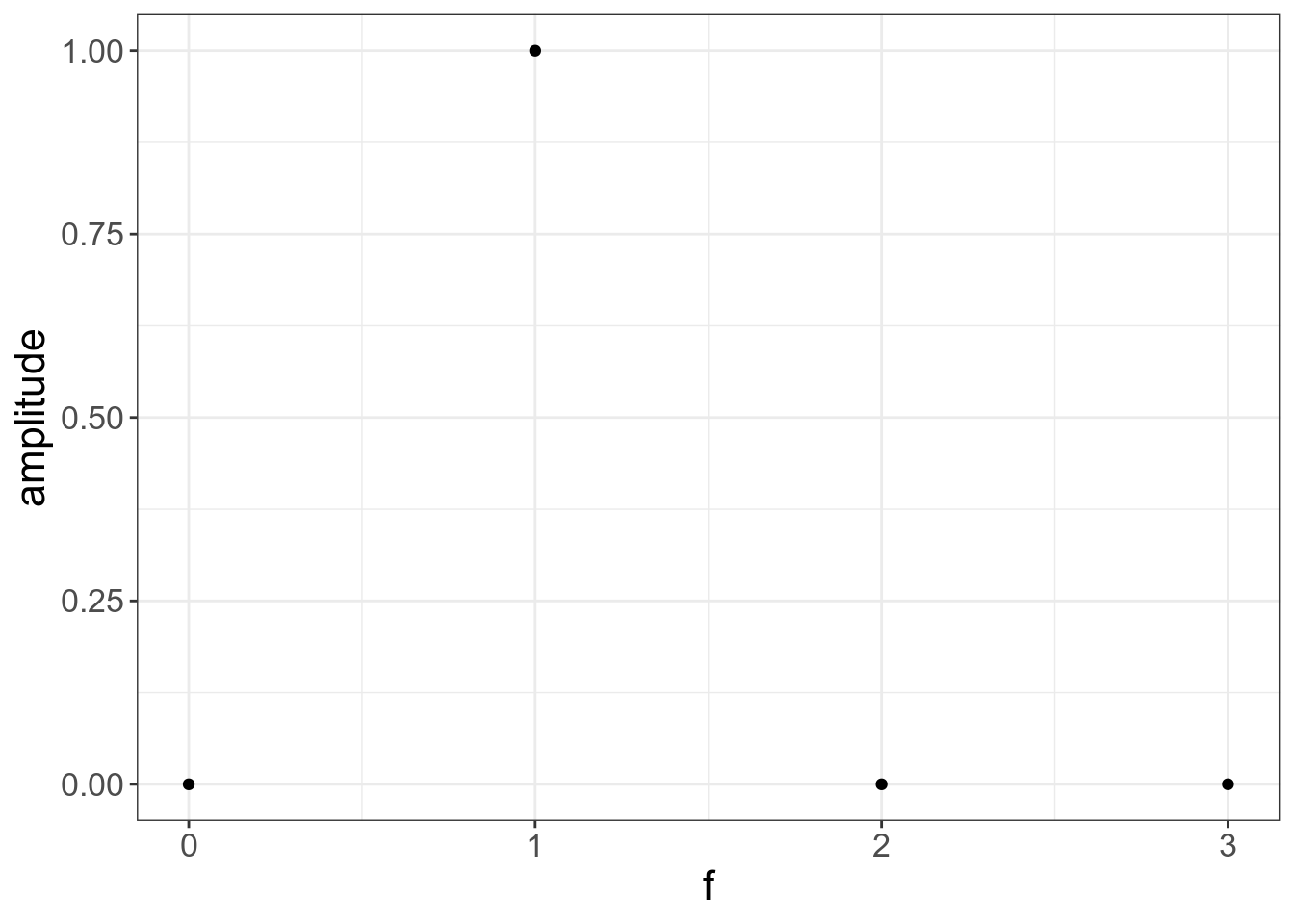

Не обязательно помнить сложную формулу, можно использовать функцию fft():

tibble(x = x,
       f = 1:length(x)-1,
       fft = fft(x)) %>% 
  ggplot(aes(f, abs(fft)))+
  geom_point()+
  scale_x_continuous(breaks = 1:length(x)-1, labels = paste(1:length(x)-1, "Hz"))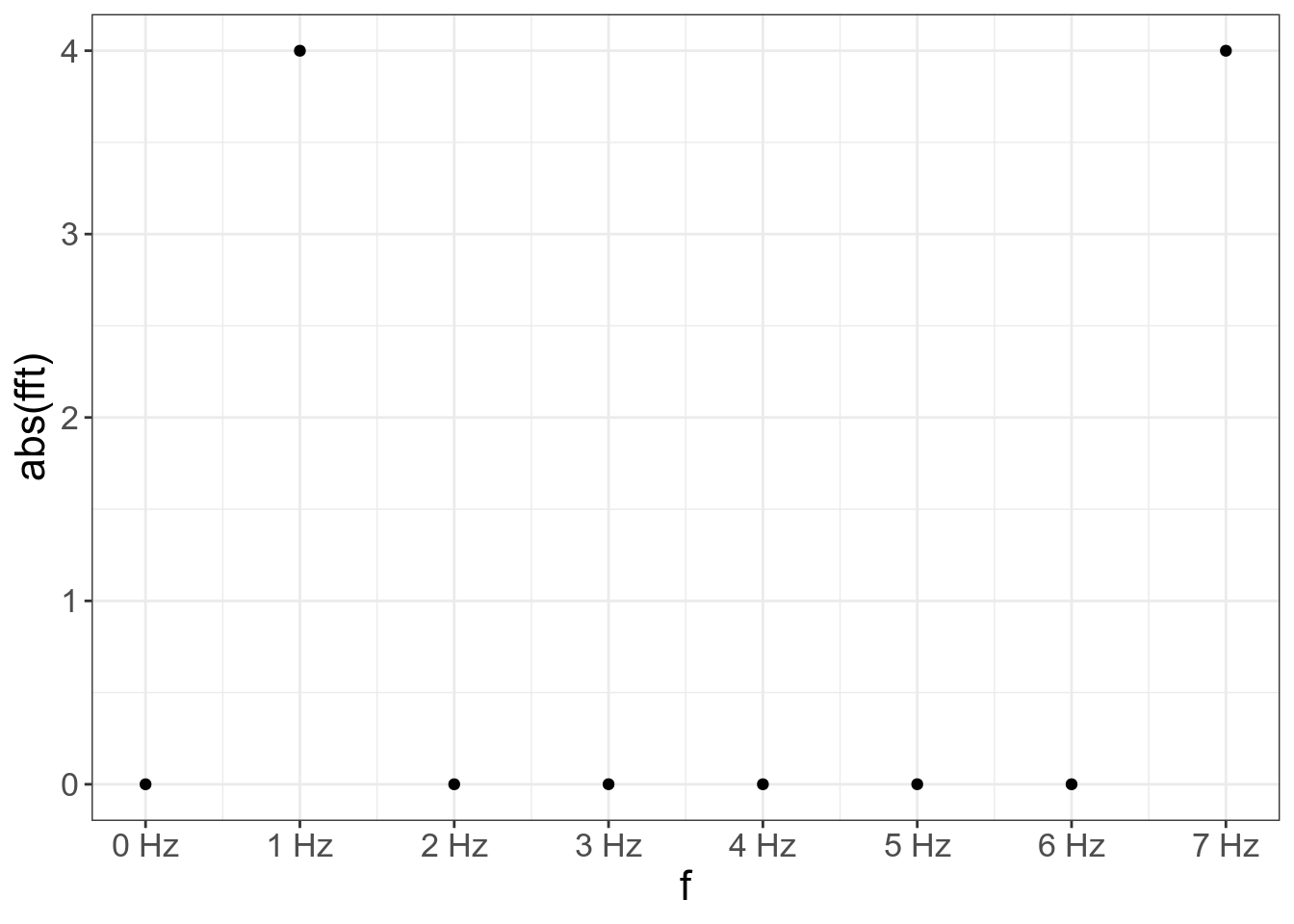

А теперь применим все преобразования:

tibble(x = x,
       f = 1:length(x)-1,
       fft = fft(x)) %>% 
  ggplot(aes(f, abs(fft)*2/length(x)))+
  geom_point()+
  xlim(0, length(x)/2-1) # это такой изящный способ получить нужное, не изменяя предыдущий код

## Warning: Removed 4 rows containing missing values (geom_point).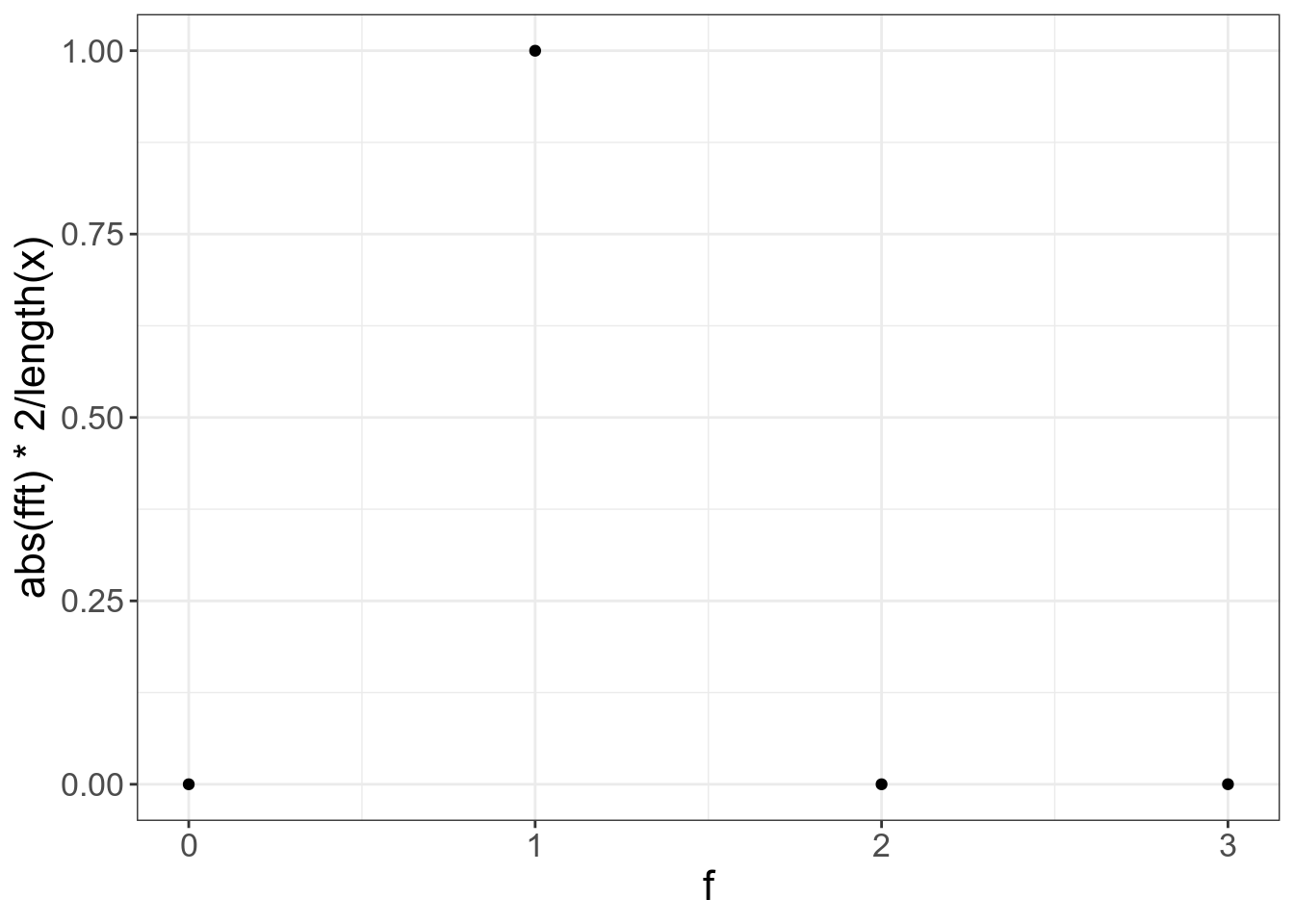

Дан ряд c(0, 3.535534, 5, 3.535534, 0, -3.535534, -5, -3.535534, 0, 3.535534, 5, 3.535534, 0, -3.535534, -5, -3.535534, 0, 3.535534, 5, 3.535534, 0, -3.535534, -5, -3.535534). Посчитайте частоту синусоиды, которая стоит за этим рядом.

Дан ряд c(0, 3.535534, 5, 3.535534, 0, -3.535534, -5, -3.535534, 0, 3.535534, 5, 3.535534, 0, -3.535534, -5, -3.535534, 0, 3.535534, 5, 3.535534, 0, -3.535534, -5, -3.535534). Посчитайте амплитуду синусоиды, которая стоит за этим рядом.

1.4 Дополнительные материалы

прекрасные материалы, сделанные Джошуа Комо про волны
13 видео, сделанные Welch Labs, про комплексные числа
материалы бесподобного Гранта Сандерсона (3blue1brown):
визуализации преобразования Фурье, сделанная Prajwal DSouza (по мотивам 3blue1brown)
визуализация преобразования Фурье, сделанная Jez Swanson
Fulop S. A. (2011) Speech Spectrum Analysis — большая книжка про спектральный анализ звука (попросите у меня .pdf)

2. Статистика или чему учат на стартовой Андана 2 недели

В фонетике данные часто выглядят как попытка предсказывать какую-то категориальную или числовую переменную на основе другой числовой переменной (переменных):

различаются долгие гласные длительностью гласного?
правда ли, что у придыхательных VOT дольше, чем у непридыхательных?
Правда ли, что гласные i и ɪ отличаются формантами?

Statistics are used much like a drunk uses a lamppost: for support, not illumination. A.E. Housman (commonly attributed to Andrew Lang)

фриквентистская vs. байесовские подходы к статистическому анализу

A frequentist uses impeccable logic to answer the wrong question, while a Bayesean answers the right question by making assumptions that nobody can fully believe in. P. G. Hammer

2.1 Тест Стьюдента

В качестве примера мы рассмотрим датасет из [Hau 2007]:

Experiment consisted of a perception and judgment test aimed at measuring the correlation between acoustic cues and perceived sexual orientation. Naïve Cantonese speakers were asked to listen to the Cantonese speech samples collected in Experiment and judge whether the speakers were gay or heterosexual. There are 14 speakers and following parameters:

[s] duration (s.duration.ms)
vowel duration (vowel.duration.ms)
fundamental frequencies mean (F0) (average.f0.Hz)
fundamental frequencies range (f0.range.Hz)
percentage of homosexual impression (perceived.as.homo)
percentage of heterosexal impression (perceived.as.hetero)
speakers orientation (orientation)
speakers age (age)

homo <- read.csv("https://raw.githubusercontent.com/agricolamz/2019_PhonDan/master/data/Hau.2007.csv")
homo

2.1.1 Одновыборочный t-test

В одной статье я нашел, что средняя длительность [s] в китайском — 56 мс. Правда ли, что данные из [Hau 2007] статистически значимо отличаются от этого значения?

Статистическая процедура:

определить H\(_0\): \(\bar{x} = \mu_o\)
определить H\(_1\): \(\bar{x} \ne \mu_o\)
определить p-value
в большинстве научных дисциплин p-value 0.05

\[t = \frac{\bar{x}-\mu_0}{\sigma/\sqrt{n}}\]

\(\sigma\) — среднеквадратическое отклонение

t.test(homo$s.duration.ms, mu = 56)

## 
##  One Sample t-test
## 
## data:  homo$s.duration.ms
## t = 2.5997, df = 13, p-value = 0.02202
## alternative hypothesis: true mean is not equal to 56
## 95 percent confidence interval:
##  56.88292 65.56565
## sample estimates:
## mean of x 
##  61.22429

2.1.2 Двухвыборочный t-test

А что если мы хотим сравнить две независимые выборки?

\[t = \frac{\bar{x}_1-\bar{x}_2}{\sqrt{\frac{\sigma^2_1}{n_1}+ \frac{\sigma^2_2}{n_2}}}\]

t.test(homo$s.duration.ms~homo$orientation)

## 
##  Welch Two Sample t-test
## 
## data:  homo$s.duration.ms by homo$orientation
## t = -1.4263, df = 11.994, p-value = 0.1793
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -13.945621   2.911336
## sample estimates:
## mean in group hetero   mean in group homo 
##             58.46571             63.98286

2.1.3 Парный t-test

Что если значения в группах связаны друг с другом? Например, настроение до нашей пары и после нашей пары

df

df %>% 
  ggplot(aes(type, value))+
  geom_point()

t.test(df$value~df$type, paired = TRUE)

## 
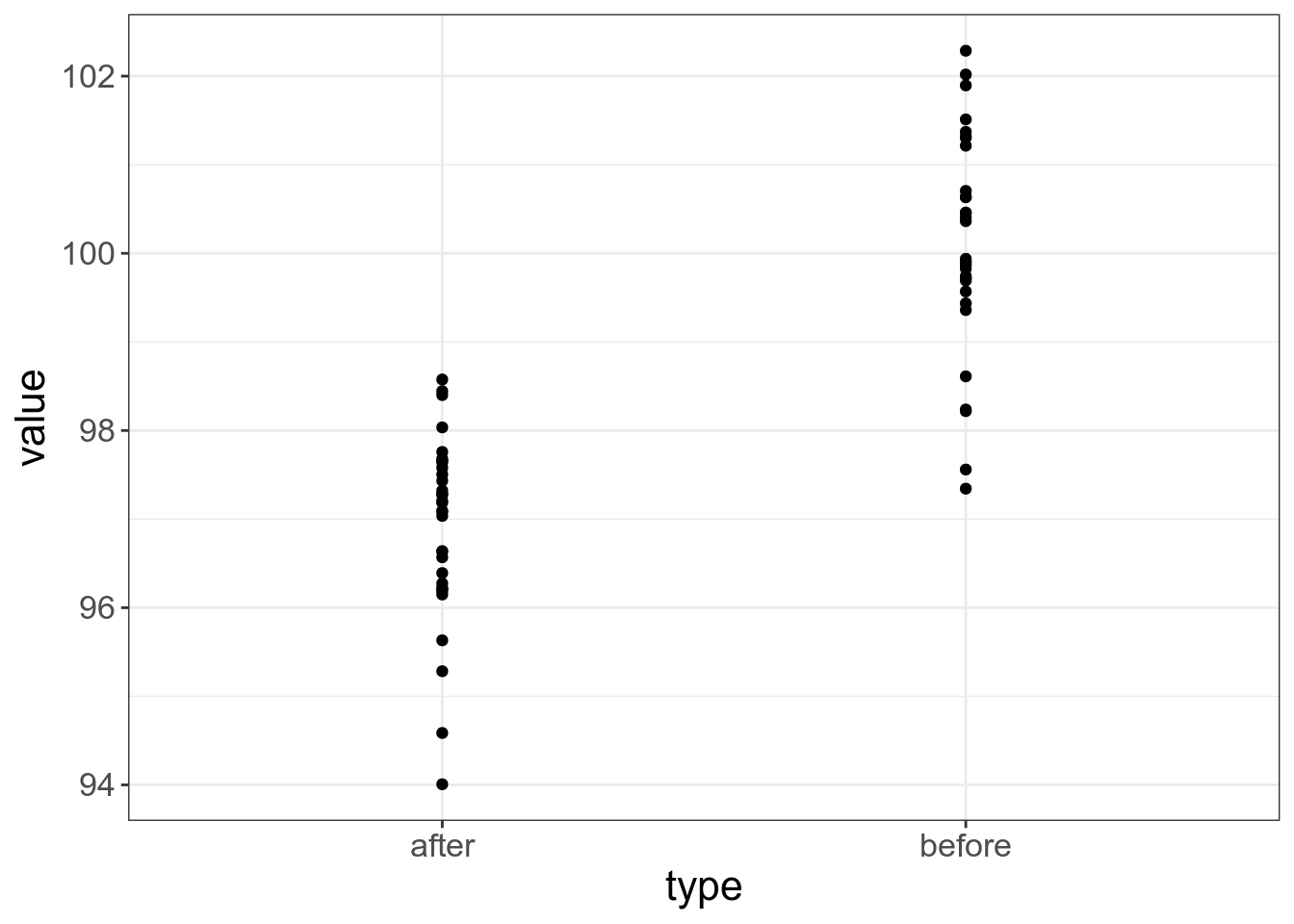
##  Paired t-test
## 
## data:  df$value by df$type
## t = -10.919, df = 31, p-value = 3.765e-12
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -3.791602 -2.598141
## sample estimates:
## mean of the differences 
##               -3.194871

2.2 Учебники по статистике для лингвистов

Butler, C. S. (1995) Statistics in Linguistics
Oakes, M. (1998) Statistics for Corpus Linguistics
Gigerenzer G. (2004) Mindless statistics
Baayen R. H. (2006) Analyzing Linguistic Data
Goodman S. (2008) A dirty dozen. twelve p-value misconceptions
Jenset G. (2008) Basic statistics for corpus linguistics
Johnson K. (2008) Quantitative_Methods_In_Linguistic
Gries S. Th. (2009) Quantitative Corpus Linguistics with R_ A Practical Introduction
Gries S. T. (2013) Statistics for linguistics with R. A practical introduction
Canning J. (2014) Statistics for the Humanities
Plonsky, L. (2015). Advancing Quantitative Methods in Second Language Research
Levshina N. (2015) How to do Linguistics with R

3 Домашнее задание

Самопроверяющаяся практика по базовому R
DFT: Дан ряд чисел: c(0, 1.11349340336624, 2.17666882281225, 3.14267963954217, 3.97135643139263, 4.63190241961315, 5.10487342908015, 5.38329297095531, 5.47282037727621, 5.39096358850103, 5.16540246342243, 4.83155754601622, 4.42959769299649, 4.00112327525573, 3.58578643762691, 3.21811420564871, 2.92478373654547, 2.7225630215062, 2.61707767889536, 2.6024992582229, 2.66217780862268, 2.77016704120256, 2.89352005708705, 2.99517282918616, 3.03718617382291, 2.98408846567984, 2.80605306823814, 2.48165702440674, 2, 1.36201226337366, 0.580843728674996, -0.318702153871827, -1.30165121735267, -2.32514793596721, -3.34137796150028, -4.30090077066292, -5.15613701605761, -5.86474273405994, -6.39261100012883, -6.71627028157747, -6.82449538527277, -6.71900789328372, -6.4142135623731, -5.93599882367669, -5.31968142882175, -4.60727575706746, -3.84428621560176, -3.07627840378181, -2.34549444740409, -1.68777484091017, -1.13002458950718, -0.688418345540212, -0.367480959782953, -0.160110980009504, -0.0485405167509005, -0.00615135766684138, 0, 0.00615135766684127, 0.0485405167509003, 0.160110980009506, 0.36748095978295, 0.68841834554021, 1.13002458950718, 1.68777484091016, 2.34549444740409, 3.07627840378181, 3.84428621560176, 4.60727575706745, 5.31968142882174, 5.93599882367669, 6.41421356237309, 6.71900789328372, 6.82449538527277, 6.71627028157747, 6.39261100012883, 5.86474273405994, 5.15613701605762, 4.30090077066293, 3.34137796150028, 2.3251479359672, 1.30165121735268, 0.318702153871841, -0.580843728674993, -1.36201226337366, -2, -2.48165702440673, -2.80605306823814, -2.98408846567985, -3.03718617382291, -2.99517282918615, -2.89352005708705, -2.77016704120256, -2.66217780862268, -2.6024992582229, -2.61707767889536, -2.7225630215062, -2.92478373654547, -3.2181142056487, -3.5857864376269, -4.00112327525574, -4.42959769299648, -4.83155754601622, -5.16540246342243, -5.39096358850103, -5.47282037727621, -5.38329297095531, -5.10487342908015, -4.63190241961315, -3.97135643139263, -3.14267963954218, -2.17666882281225, -1.11349340336623). Проведите дискретное преобразование Фурье и приведите значение частоты с наибольшей амплитудой:

DFT: Дан ряд чисел: c(0, 1.11349340336624, 2.17666882281225, 3.14267963954217, 3.97135643139263, 4.63190241961315, 5.10487342908015, 5.38329297095531, 5.47282037727621, 5.39096358850103, 5.16540246342243, 4.83155754601622, 4.42959769299649, 4.00112327525573, 3.58578643762691, 3.21811420564871, 2.92478373654547, 2.7225630215062, 2.61707767889536, 2.6024992582229, 2.66217780862268, 2.77016704120256, 2.89352005708705, 2.99517282918616, 3.03718617382291, 2.98408846567984, 2.80605306823814, 2.48165702440674, 2, 1.36201226337366, 0.580843728674996, -0.318702153871827, -1.30165121735267, -2.32514793596721, -3.34137796150028, -4.30090077066292, -5.15613701605761, -5.86474273405994, -6.39261100012883, -6.71627028157747, -6.82449538527277, -6.71900789328372, -6.4142135623731, -5.93599882367669, -5.31968142882175, -4.60727575706746, -3.84428621560176, -3.07627840378181, -2.34549444740409, -1.68777484091017, -1.13002458950718, -0.688418345540212, -0.367480959782953, -0.160110980009504, -0.0485405167509005, -0.00615135766684138, 0, 0.00615135766684127, 0.0485405167509003, 0.160110980009506, 0.36748095978295, 0.68841834554021, 1.13002458950718, 1.68777484091016, 2.34549444740409, 3.07627840378181, 3.84428621560176, 4.60727575706745, 5.31968142882174, 5.93599882367669, 6.41421356237309, 6.71900789328372, 6.82449538527277, 6.71627028157747, 6.39261100012883, 5.86474273405994, 5.15613701605762, 4.30090077066293, 3.34137796150028, 2.3251479359672, 1.30165121735268, 0.318702153871841, -0.580843728674993, -1.36201226337366, -2, -2.48165702440673, -2.80605306823814, -2.98408846567985, -3.03718617382291, -2.99517282918615, -2.89352005708705, -2.77016704120256, -2.66217780862268, -2.6024992582229, -2.61707767889536, -2.7225630215062, -2.92478373654547, -3.2181142056487, -3.5857864376269, -4.00112327525574, -4.42959769299648, -4.83155754601622, -5.16540246342243, -5.39096358850103, -5.47282037727621, -5.38329297095531, -5.10487342908015, -4.63190241961315, -3.97135643139263, -3.14267963954218, -2.17666882281225, -1.11349340336623). Проведите дискретное преобразование Фурье и приведите значение амплитуды для наблюдения с наибольшей частотой и ненулевой амплитудой:

t-test: Это задание основано на работе (Coretta 2017, https://goo.gl/NrfgJm). В этой диссертации рассматривается отношения между длительностью гласного и придыхание согласного. Автор собрал данные 5 носителей исланского. Дальше он извлек длительность гласного, после которого были придыхательные и непридыхательные. Проверьте, правда ли, что гласные перед аспирированныем согласными статистикали значимо короче гласных после которых непридыхательные. Данные можно скачать так: read.csv("https://raw.githubusercontent.com/agricolamz/2019_PhonDan/master/data/Coretta_2017_icelandic.csv"). В ответе приведите t-статистику c точностью до трех знаков после запятой: