2 Введение в R

2.1 Наука о данных

Наука о данных — это новая область знаний, которая активно развивается в последнее время. Она находиться на пересечении компьютерных наук, статистики и математики, и трудно сказать, действительно ли это наука. При этом это движение развивается в самых разных научных направлениях, иногда даже оформляясь в отдельную отрасль:

  • биоинформатика
  • вычислительная криминалистика
  • цифровые гуманитарные исследования
  • датажурналистика
  • …

Все больше книг “Data Science for …”:

Среди умений датасаентистов можно перечислить следующие:

  • сбор и обработка данных
  • трансформация данных
  • визуализация данных
  • статистическое моделирование данных
  • представление полученных результатов
  • организация всей работы воспроизводимым способом

Большинство этих тем в той или иной мере будет представлено в нашем курсе.

2.2 Установка R и RStudio

В данной книге используется исключительно R (R Core Team 2019), так что для занятий понадобятся:

  • R
    • на Windows
    • на Mac
    • на Linux, также можно добавить зеркало и установить из командной строки:
sudo apt-get install r-cran-base

Часто можно увидеть или услышать, что R — язык программирования для “статистической обработки данных.” Изначально это, конечно, было правдой, но уже давно R — это полноценный язык программирования, который при помощи своих пакетов позволяет решать огромный спектр задач. В данной книге используется следующая версия R:

## [1] "R version 4.1.0 (2021-05-18)"

Некоторые люди не любят устанавливать лишние программы себе на компьютер, несколько вариантов есть и для них:

  • RStudio cloud — полная функциональность RStudio, пока бесплатная, но скоро это исправят;
  • RStudio on rollApp — облачная среда, позволяющая разворачивать программы.

Первый и вполне закономерный вопрос: зачем мы ставили R и отдельно еще какой-то RStudio? Если опустить незначительные детали, то R — это сам язык программирования, а RStudio — это среда (IDE), которая позволяет в этом языке очень удобно работать.

2.3 Полезные ссылки

В интернете легко найти документацию и туториалы по самым разным вопросам в R, так что главный залог успеха — грамотно пользоваться поисковиком, и лучше на английском языке.

2.4 Rstudio

Когда вы откроете RStudio первый раз, вы увидите три панели: консоль, окружение и историю, а также панель для всего остального. Если ткнуть в консоли на значок уменьшения, то можно открыть дополнительную панель, где можно писать скрипт.

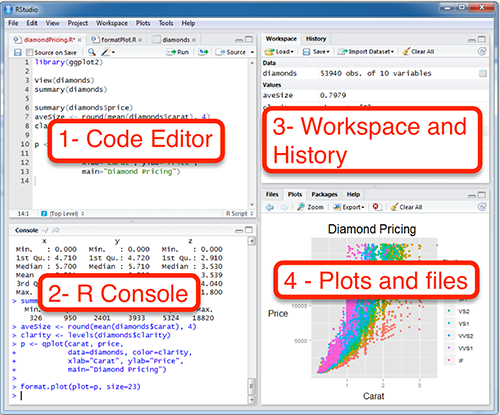
Существуют разные типы пользователей: одни любят работать в консоли (на картинке это 2 — R Console), другие предпочитают скрипты (1 — Code Editor). Консоль позволяет использовать интерактивный режим команда-ответ, а скрипт является по сути текстовым документом, фрагменты которого можно для отладки запускать в консоли.

3 — Workspace and History: Здесь можно увидеть переменные. Это поле будет автоматически обновляться по мере того, как Вы будете запускать строчки кода и создавать новые переменные. Еще там есть вкладка с историей последних команд, которые были запущены.

4 — Plots and files: Здесь есть очень много всего. Во-первых, небольшой файловый менеджер, во-вторых, там будут появляться графики, когда вы будете их рисовать. Там же есть вкладка с вашими пакетами (Packages) и Help по функциям. Но об этом потом.

2.5 Введение в R

2.5.1 R как калькулятор

Ой-ей, консоль, скрипт че-то все непонятно.
Давайте начнем с самого простого и попробуем использовать R как простой калькулятор. +, -, *, /, ^ (степень), () и т.д.

Просто запускайте в консоли пока не надоест:

40 + 2
## [1] 42
3 - 2
## [1] 1
5 * 6
## [1] 30
99 / 9
## [1] 11
2 ^ 3
## [1] 8
(2 + 2) * 2
## [1] 8

Ничего сложного, верно? Вводим выражение и получаем результат. Порядок выполнения арифметических операций как в математике, так что не забывайте про скобочки. Подсказку по порядку выполнения операций в R можно получить с помощью следующей команды:

?Syntax

Если Вы не уверены в том, какие операции имеют приоритет, то используйте скобочки, чтобы точно обозначить, в каком порядке нужно производить операции.

2.5.2 Функции

Давайте теперь извлечем корень из какого-нибудь числа. В принципе, тем, кто помнит школьный курс математики, возведения в степень вполне достаточно:

16 ^ 0.5
## [1] 4

Ну а если нет, то можете воспользоваться специальной функцией: это обычно какие-то буквенные символы с круглыми скобками сразу после названия функции. Мы подаем на вход (внутрь скобочек) какие-то данные, внутри этих функций происходят какие-то вычисления, которые выдают в ответ какие-то другие данные (или же функция записывает файл, рисует график и т.д.).

Данные на входе называются аргументом функции, а иногда — параметром функции. В обыденной речи часто говорят инпут (калька с английского input).

Вот, например, функция для корня:

sqrt(16)
## [1] 4

R — case-sensitive язык, т.е. регистр важен. SQRT(16) не будет работать.

А вот так выглядит функция логарифма:

log(8)
## [1] 2.079442

Так, вроде бы все нормально, но… Если Вы еще что-то помните из школьной математики, то должны понимать, что что-то здесь не так.

Здесь не хватает основания логарифма!

Логарифм — показатель степени, в которую надо возвести число, называемое основанием, чтобы получить данное число.

То есть у логарифма 8 по основанию 2 будет значение 3:

\(\log_2 8 = 3\)

То есть если возвести 2 в степень 3 у нас будет 8:

\(2^3 = 8\)

Только наша функция считает все как-то не так.

Чтобы понять, что происходит, нам нужно залезть в хэлп этой функции:

?log

Справа внизу в RStudio появится вот такое окно:

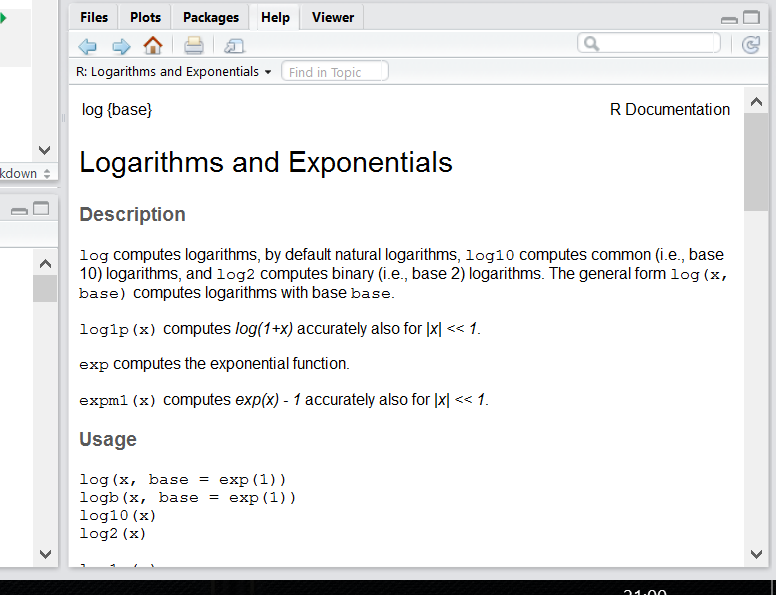
Действительно, у этой функции есть еще аргумент base =. По умолчанию он равен числу Эйлера (2.7182818…), т.е. функция считает натуральный логарифм. В большинстве функций R есть какой-то основной инпут — данные в том или ином формате, а есть и дополнительные параметры, которые можно прописывать вручную, если параметры по умолчанию вас не устраивают.

log(x = 8, base = 2)
## [1] 3

…или просто (если Вы уверены в порядке аргументов):

log(8, 2)
## [1] 3

Более того, Вы можете использовать результат выполнения одних функций в качестве аргумента для других:

log(8, sqrt(4))
## [1] 3

Если эксплицитно писать имена аргументов, то их порядок в функции не важен:

log(base = 2, x = 8)
## [1] 3

А еще можно недописывать имена аргументов, если они не совпадают с другими:

log(b = 2, x = 8)
## [1] 3

Мы еще много раз будем возвращаться к функциям. Вообще, функции — это одна из важнейших штук в R (примерно так же как и в Python). Мы будем создавать свои функции, использовать функции как инпут для функций и многое-многое другое. В R очень крутые возможности работы с функциями. Поэтому подружитесь с функциями, они клевые.

Арифметические знаки, которые мы использовали: +,-,/,^ и т.д. называются операторами и на самом деле тоже являются функциями:

'+'(3,4)
## [1] 7

2.5.3 Переменные

Важная штука в программировании на практически любом языке — возможность сохранять значения в переменных. В R это обычно делается с помощью вот этих символов: <- (но можно использовать и обычное =, хотя это не очень принято). Для этого есть удобное сочетание клавиш: нажмите одновременно Alt - (или option - на Маке).

a <- 2
a
## [1] 2

Справа от <- находится значение, которое вы хотите сохранить, или же какое-то выражение, результат которого вы хотите сохранить в эту переменную1:

a <- log(9, 3)

Слева от <- находится название будущей переменной. Название переменных может быть самым разным. Есть несколько ограничений для синтаксически валидных имен переменных: они должны включать в себя буквы, цифры, . или _, начинаться на букву (или точку, за которой не будет следовать цифра), не должны совпадать с коротким списком зарезервированных слов. Короче говоря, название не должно включать в себя пробелы и большинство других знаков.

Нельзя: - new variable - _new_variable - .1var - v-r

Можно: - new_variable - .new.variable - var_2

Обязательно делайте названия переменных осмысленными! Старайтесь делать при этом их понятными и короткими, это сохранит вам очень много времени, когда вы (или кто-то еще) будете пытаться разобраться в написанном ранее коде. Если название все-таки получается длинным и состоящим из нескольких слов, то лучше всего использовать нижнее подчеркивание в качестве разделителя: some_variable2.

После присвоения переменная появляется во вкладке Environment в RStudio:

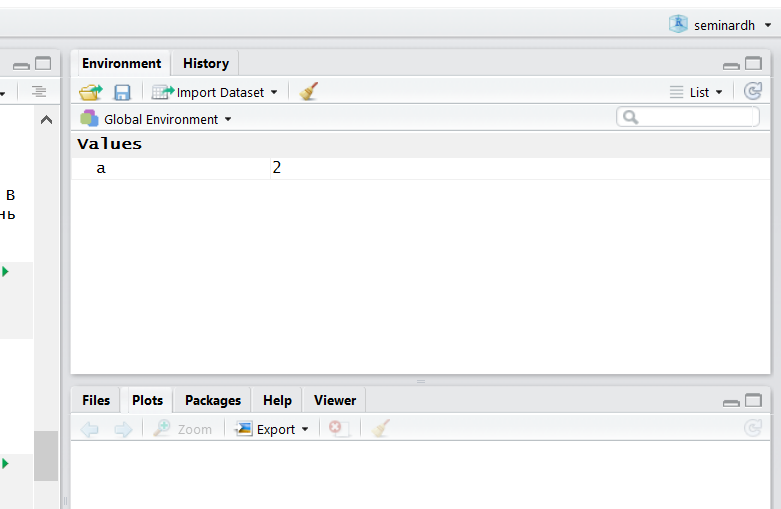
Можно использовать переменные в функциях и просто вычислениях:

b <- a ^ a + a * a
b
## [1] 8
log(b, a)
## [1] 3

2.6 Логические операторы

Вы можете сравнивать разные переменные:

a == b
## [1] FALSE

Заметьте, что сравнивая две переменные мы используем два знака равно ==, а не один =. Иначе это будет означать присвоение.

a = b #присвоение, а не сравнение!
a
## [1] 8
b
## [1] 8

Теперь Вы сможете понять комикс про восстание роботов на следующей странице (пусть он и совсем про другой язык программирования)

Этот комикс объясняет, как важно не путать присваивание и сравнение (хотя я иногда путаю до сих пор =( ).

Иногда нам нужно проверить на неравенство:

a <- 2
b <- 3

a == b
## [1] FALSE
a != b
## [1] TRUE

Восклицательный язык в программировании вообще и в R в частности стандартно означает отрицание.

Еще мы можем сравнивать на больше/меньше:

a > b
## [1] FALSE
a < b
## [1] TRUE
a >= b
## [1] FALSE
a <= b
## [1] TRUE

Этим мы будем пользоваться в дальнейшем регулярно! Именно на таких простых логических операциях построено большинство операций с данными.

2.7 Типы данных

До этого момента мы работали только с числами (numeric):

class(a)
## [1] "numeric"

На самом деле, в R три типа numeric: integer (целые), double (дробные), complex (комплексные числа)3. R сам будет конвертировать числа в нужный тип numeric при необходимости, поэтому этим можно не заморачиваться.

Если же все-таки нужно задать конкретный тип числа эксплицитно, то можно воспользоваться функциями as.integer(), as.double() и as.complex(). Кроме того, при создании числа можно поставить в конце L, чтобы обозначить число как integer:

is.integer(5)
## [1] FALSE
is.integer(5L)
## [1] TRUE

Про double есть еще один маленький секрет. Дело в том, что дробные числа хранятся в R как числа с плавающей запятой двойной точности. Дробные числа в компьютере могут быть записаны только с определенной степенью точности, поэтому иногда встречаются вот такие вот ситуации:

sqrt(2)^2 == 2
## [1] FALSE

Это довольно стандартная ситуация, характерная не только для R. Чтобы ее избежать, можно воспользоваться функцией all.equal():

all.equal(sqrt(2)^2, 2)
## [1] TRUE

Теперь же нам нужно ознакомиться с двумя другими важными типами данных в R:

  1. character: строки символов. Они должны выделяться кавычками.
s <- 'Всем привет!'
s
## [1] "Всем привет!"
class(s)
## [1] "character"

Можно использовать как ", так и ' (что удобно, когда строчка внутри уже содержит какие-то кавычки).

"Ph'nglui mglw'nafh Cthulhu R'lyeh wgah'nagl fhtagn"
## [1] "Ph'nglui mglw'nafh Cthulhu R'lyeh wgah'nagl fhtagn"
  1. logical: просто TRUE или FALSE.
t1 <- TRUE
f1 <- FALSE

t1
## [1] TRUE
f1
## [1] FALSE

Вообще, можно еще писать T и F (но не True и False!).

t2 <- T
f2 <- F

Это дурная практика, так как R защищает от перезаписи переменные TRUE и FALSE, но не защищает от этого T и F.

TRUE <- FALSE
## Error in TRUE <- FALSE: invalid (do_set) left-hand side to assignment
TRUE
## [1] TRUE
T <- FALSE
T
## [1] FALSE

Мы уже встречались с логическими значениями при сравнении двух числовых переменных. Теперь вы можете догадаться, что результаты сравнения, например, числовых или строковых переменных, можно тоже сохранять в переменные!

comparison <- a == b
comparison
## [1] FALSE

Это нам очень понадобится, когда мы будем работать с реальными данными: нам нужно будет постоянно вытаскивать какие-то данные из датасета, что как раз и построено на игре со сравнением переменных.

Чтобы этим хорошо уметь пользоваться, нам нужно еще освоить как работать с логическими операторами. Про один мы немного уже говорили — это логическое НЕ (!). ! превращает TRUE в FALSE, а FALSE в TRUE:

t1
## [1] TRUE
!t1
## [1] FALSE
!!t1 #Двойное отрицание!
## [1] TRUE

Еще есть логическое И (выдаст TRUE только в том случае если обе переменные TRUE):

t1 & t2
## [1] TRUE
t1 & f1
## [1] FALSE

А еще логическое ИЛИ (выдаст TRUE в случае если хотя бы одна из переменных TRUE):

t1 | f1
## [1] TRUE
f1 | f2
## [1] FALSE

Если кому-то вдруг понадобится другое ИЛИ (строгое ЛИБО) — есть функция xor(), принимающая два аргумента.

Итак, мы только что разобрались с самой занудной (хотя и важной) частью - с основными типа данных в R и как с ними работать4. Пора переходить к чему-то более интересному и специфическому для R. Вперед к ВЕКТОРАМ!

2.8 Вектор

Если у вас не было линейной алгебры (или у вас с ней было все плохо), то просто запомните, что вектор (или atomic vector или atomic) — это набор (столбик) чисел в определенном порядке.

Если вы привыкли из школьного курса физики считать вектора стрелочками, то не спешите возмущаться и паниковать. Представьте стрелочки как точки из нуля координат {0,0} до какой-то точки на координатной плоскости, например, {2,3}:

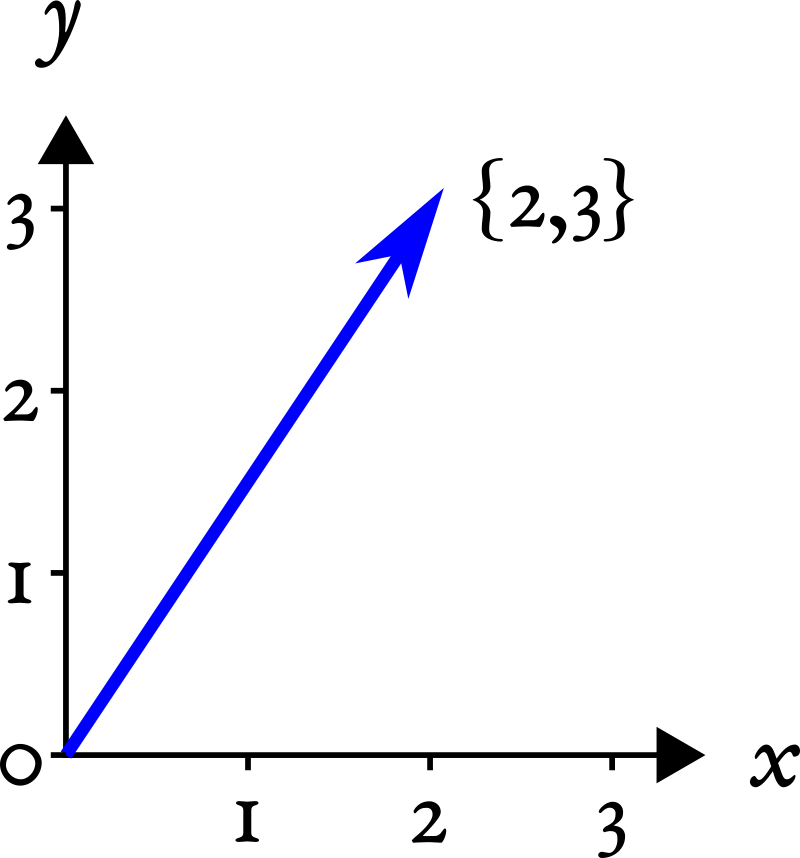
Вот последние два числа и будем считать вектором. Попытайтесь теперь мысленно стереть координатную плоскость и выбросить стрелочки из головы, оставив только последовательность чисел {2,3}:

На самом деле, мы уже работали с векторами в R, но, возможно, вы об этом даже не догадывались. Дело в том, что в R нет как таковых “значений,” есть вектора длиной 1. Такие дела!

Чтобы создать вектор из нескольких значений, нужно воспользоваться функцией c():

c(4, 8, 15, 16, 23, 42)
## [1]  4  8 15 16 23 42
c("Хэй", "Хэй", "Ха")
## [1] "Хэй" "Хэй" "Ха"

Одна из самых мерзких и раздражающих причин ошибок в коде — это использование с из кириллицы вместо c из латиницы. Видите разницу? И я не вижу. А R видит. И об этом сообщает:

с(3, 4, 5)
## Error in с(3, 4, 5): could not find function "с"

Для создания числовых векторов есть удобный оператор :

1:10
##  [1]  1  2  3  4  5  6  7  8  9 10
5:-3
## [1]  5  4  3  2  1  0 -1 -2 -3

Этот оператор создает вектор от первого числа до второго с шагом 1. Вы не представляете, как часто эта штука нам пригодится… Если же нужно сделать вектор с другим шагом, то есть функция seq():

seq(10, 100, by = 10)
##  [1]  10  20  30  40  50  60  70  80  90 100

Кроме того, можно задавать не шаг, а длину вектора. Тогда шаг функция seq() посчитает сама:

seq(1, 13, length.out = 4)
## [1]  1  5  9 13

Другая функция — rep() — позволяет создавать вектора с повторяющимися значениями. Первый аргумент — значение, которое нужно повторять, а второй аргумент — сколько раз повторять.

rep(1, 5)
## [1] 1 1 1 1 1

И первый, и второй аргумент могут быть векторами!

rep(1:3, 3)
## [1] 1 2 3 1 2 3 1 2 3
rep(1:3, 1:3)
## [1] 1 2 2 3 3 3

Еще можно объединять вектора (что мы, по сути, и делали, просто с векторами длиной 1):

v1 <- c("Hey", "Ho")
v2 <- c("Let's", "Go!")
c(v1, v2)
## [1] "Hey"   "Ho"    "Let's" "Go!"

2.8.1 Приведение типов

Что будет, если вы объедините два вектора с значениями разных типов? Ошибка?

Мы уже обсуждали, что в atomic может быть только один тип данных. В некоторых языках программирования при операции с данными разных типов мы бы получили ошибку. А вот в R при несовпадении типов пройзойдет попытка привести типы к “общему знаменателю,” то есть конвертировать данные в более “широкий” тип.

Например:

c(FALSE, 2)
## [1] 0 2

FALSE превратился в 0 (а TRUE превратился бы в 1), чтобы оба значения можно было объединить в вектор. То же самое произошло бы в случае операций с векторами:

2 + TRUE
## [1] 3

Это называется неявным приведением типов (implicit coercion).

Вот более сложный пример:

c(TRUE, 3, "Привет")
## [1] "TRUE"   "3"      "Привет"

У R есть иерархия приведения типов:

NULL < raw < logical < integer < double < complex < character < list < expression.

Мы из этого списка еще многого не знаем, сейчас важно запомнить, что логические данные — TRUE и FALSE — превращаются в 0 и 1 соответственно, а 0 и 1 в строчки "0" и "1".

Если Вы боитесь полагаться на приведение типов, то можете воспользоваться функциями as.нужныйтипданных для явного приведения типов (explicit coercion):

as.numeric(c(T, F, F))
## [1] 0 0 0
as.character(as.numeric(c(T, F, F)))
## [1] "0" "0" "0"

Можно превращать и обратно, например, строковые значения в числовые. Если среди числа встретится буква или другой неподходящий знак, то мы получим предупреждение NA — пропущенное значение (мы очень скоро научимся с ними работать).

as.numeric(c("1", "2", "три"))
## Warning: NAs introduced by coercion
## [1]  1  2 NA

Один из распространенных примеров использования неявного приведения типов — использования функций sum() и mean() для подсчета в логическом векторе количества и доли TRUE соответсвенно. Мы будем много раз пользоваться этим приемом в дальнейшем!

2.8.2 Векторизация

Все те арифметические операторы, что мы использовали ранее, можно использовать с векторами одинаковой длины:

n <- 1:4
m <- 4:1
n + m
## [1] 5 5 5 5
n - m
## [1] -3 -1  1  3
n * m
## [1] 4 6 6 4
n / m
## [1] 0.2500000 0.6666667 1.5000000 4.0000000
n ^ m + m * (n - m)
## [1] -11   5  11   7

Если применить операторы на двух векторах одинаковой длины, то мы получим результат поэлементного применения оператора к двум векторам. Это называется векторизацией (vectorization).

Если после какого-нибудь MATLAB Вы привыкли, что по умолчанию операторы работают по правилам линейной алгебры и m*n будет давать скалярное произведение (dot product), то снова нет. Для скалярного произведения нужно использовать операторы с % по краям:

n %*% m
##      [,1]
## [1,]   20

Абсолютно так же и с операциями с матрицами в R, хотя про матрицы будет немного позже.

В принципе, большинство функций в R, которые работают с отдельными значениями, так же хорошо работают и с целыми векторами. Скажем, Вы хотите извлечь корень из нескольких чисел, для этого не нужны никакие циклы (как это обычно делается в других языках программирования). Можно просто “скормить” вектор функции и получить результат применения функции к каждому элементу вектора:

sqrt(1:10)
##  [1] 1.000000 1.414214 1.732051 2.000000 2.236068 2.449490 2.645751 2.828427
##  [9] 3.000000 3.162278

Таких векторизованных функций в R очень много. Многие из них написаны на более низкоуровневых языках программирования (C, C++, FORTRAN), за счет чего использование таких функций приводит не только к более элегантному, лаконичному, но и к более быстрому коду.

Векторизация в R — это очень важная фишка, которая отличает этот язык программирования от многих других. Если вы уже имеете опыт программирования на другом языке, то вам во многих задачах захочется использовать циклы типа for и while 4.2. Не спешите этого делать! В очень многих случаях циклы можно заменить векторизацией. Тем не менее, векторизация — это не единственный способ избавить от циклов типа for и while 5.5.1.

2.8.3 Ресайклинг

Допустим мы хотим совершить какую-нибудь операцию с двумя векторами. Как мы убедились, с этим обычно нет никаких проблем, если они совпадают по длине. А что если вектора не совпадают по длине? Ничего страшного! Здесь будет работать правило ресайклинга (правило переписывания, recycling rule). Это означает, что если мы делаем операцию на двух векторах разной длины, то если короткий вектор кратен по длине длинному, короткий вектор будет повторяться необходимое количество раз:

n <- 1:4
m <- 1:2
n * m
## [1] 1 4 3 8

А что будет, если совершать операции с вектором и отдельным значением? Можно считать это частным случаем ресайклинга: короткий вектор длиной 1 будет повторятся столько раз, сколько нужно, чтобы он совпадал по длине с длинным:

n * 2
## [1] 2 4 6 8

Если же меньший вектор не кратен большему (например, один из них длиной 3, а другой длиной 4), то R посчитает результат, но выдаст предупреждение.

n + c(3,4,5)
## Warning in n + c(3, 4, 5): longer object length is not a multiple of shorter
## object length
## [1] 4 6 8 7

Проблема в том, что эти предупреждения могут в неожиданный момент стать причиной ошибок. Поэтому не стоит полагаться на ресайклинг некратных по длине векторов. См. здесь. А вот ресайклинг кратных по длине векторов — это очень удобная штука, которая используется очень часто.

2.8.4 Индексирование векторов

Итак, мы подошли к одному из самых сложных моментов. И одному из основных. От того, как хорошо вы научись с этим работать, зависит весь Ваш дальнейший успех на R-поприще!

Речь пойдет об индексировании векторов. Задача, которую Вам придется решать каждые пять минут работы в R - как выбрать из вектора (или же списка, матрицы и датафрейма) какую-то его часть. Для этого используются квадратные скобочки [] (не круглые - они для функций!).
Самое простое - индексировать по номеру индекса, т.е. порядку значения в векторе.

n <- 1:10
n[1]
## [1] 1
n[10]
## [1] 10

Если вы знакомы с другими языками программирования (не MATLAB, там все так же) и уже научились думать, что индексация с 0 — это очень удобно и очень правильно (ну или просто свыклись с этим), то в R Вам придется переучиться обратно. Здесь первый индекс — это 1, а последний равен длине вектора — ее можно узнать с помощью функции length(). С обоих сторон индексы берутся включительно.

С помощью индексирования можно не только вытаскивать имеющиеся значения в векторе, но и присваивать им новые:

n[3] <- 20
n
##  [1]  1  2 20  4  5  6  7  8  9 10

Конечно, можно использовать целые векторы для индексирования:

n[4:7]
## [1] 4 5 6 7
n[10:1]
##  [1] 10  9  8  7  6  5  4 20  2  1

Индексирование с минусом выдаст вам все значения вектора кроме выбранных:

n[-1]
## [1]  2 20  4  5  6  7  8  9 10
n[c(-4, -5)]
## [1]  1  2 20  6  7  8  9 10

Минус здесь “выключает” выбранные значения из вектора, а не означает отсчет с конца как в Python.

Более того, можно использовать логический вектор для индексирования. В этом случае нужен логический вектор такой же длины:

n[c(TRUE, FALSE, TRUE, FALSE, TRUE, FALSE, TRUE, FALSE, TRUE, FALSE)]
## [1]  1 20  5  7  9

Логический вектор работает здесь как фильтр: пропускает только те значения, где на соответствующей позиции в логическом векторе для индексирования содержится TRUE, и не пропускает те значения, где на соответствующей позиции в логическом векторе для индексирования содержится FALSE.

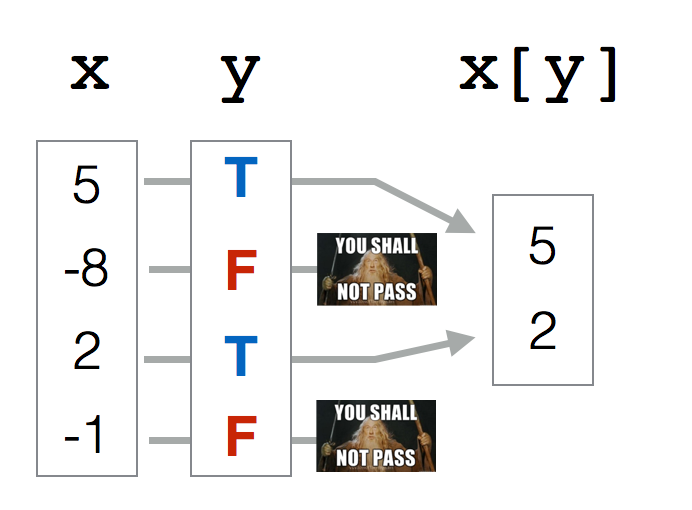
Ну а если эти два вектора (исходный вектор и логический вектор индексов) не равны по длине, то тут будет снова работать правило ресайклинга!

n[c(TRUE, FALSE)] #то же самое - recycling rule!
## [1]  1 20  5  7  9

Есть еще один способ индексирования векторов, но он несколько более редкий: индексирование по имени. Дело в том, что для значений векторов можно (но не обязательно) присваивать имена:

my_named_vector <- c(first = 1,
                     second = 2,
                     third = 3)
                     my_named_vector['first']
## first 
##     1

А еще можно “вытаскивать” имена из вектора с помощью функции names() и присваивать таким образом новые имена.

d <- 1:4
names(d) <- letters[1:4]
d["a"]
## a 
## 1

letters - это “зашитая” в R константа - вектор букв от a до z. Иногда это очень удобно! Кроме того, есть константа LETTERS - то же самое, но заглавными буквами. А еще в R есть названия месяцев на английском и числовая константа pi.

Теперь посчитаем среднее вектора n:

mean(n)
## [1] 7.2

А как вытащить все значения, которые больше среднего?

Сначала получим логический вектор — какие значения больше среднего:

larger <- n > mean(n)
larger
##  [1] FALSE FALSE  TRUE FALSE FALSE FALSE FALSE  TRUE  TRUE  TRUE

А теперь используем его для индексирования вектора n:

n[larger]
## [1] 20  8  9 10

Можно все это сделать в одну строчку:

n[n>mean(n)]
## [1] 20  8  9 10

Предыдущая строчка отражает то, что мы будем постоянно делать в R: вычленять (subset) из данных отдельные куски на основании разных условий.

2.8.5 NA — пропущенные значения

В реальных данных у нас часто чего-то не хватает. Например, из-за технической ошибки или невнимательности не получилось записать какое-то измерение. Для обозначения пропущенных значений в R есть специальное значение NA. NA — это не строка "NA", не 0, не пустая строка "" и не FALSE. NA — это NA. Большинство операций с векторами, содержащими NA будут выдавать NA:

missed <- NA
missed == "NA"
## [1] NA
missed == ""
## [1] NA
missed == NA
## [1] NA

Заметьте: даже сравнение NA c NA выдает NA!

Иногда NA в данных очень бесит:

n[5] <- NA
n
##  [1]  1  2 20  4 NA  6  7  8  9 10
mean(n)
## [1] NA

Что же делать?
Наверное, надо сравнить вектор с NA и исключить этих пакостников. Давайте попробуем:

n == NA
##  [1] NA NA NA NA NA NA NA NA NA NA

Ах да, мы ведь только что узнали, что даже сравнение NA c NA приводит к NA!

Чтобы выбраться из этой непростой ситуации, используйте функцию is.na():

is.na(n)
##  [1] FALSE FALSE FALSE FALSE  TRUE FALSE FALSE FALSE FALSE FALSE

Результат выполнения is.na(n) выдает FALSE в тех местах, где у нас числа и TRUE там, где у нас NA. Чтобы вычленить из вектора n все значения кроме NA нам нужно, чтобы было наоборот: TRUE, если это не NA, FALSE, если это NA. Здесь нам понадобится логический оператор НЕ ! (мы его уже встречали), который инвертирует логические значения:

n[!is.na(n)]
## [1]  1  2 20  4  6  7  8  9 10

Ура, мы можем считать среднее!

mean(n[!is.na(n)])
## [1] 7.444444

Теперь Вы понимаете, зачем нужно отрицание (!)

Вообще, есть еще один из способов посчитать среднее, если есть NA. Для этого надо залезть в хэлп по функции mean():

?mean()

В хэлпе мы найдем параметр na.rm =, который по умолчанию FALSE. Вы знаете, что нужно делать!

mean(n, na.rm = TRUE)
## [1] 7.444444

NA может появляться в векторах других типов тоже. На самом деле, NA - это специальное значение в логических векторах, тогда как в векторах других типов NA появляется как NA_integer_, NA_real_, NA_complex_ или NA_character_, но R обычно сам все переводит в нужный формат и показывает как просто NA.
Кроме NA есть еще NaN — это разные вещи. NaN расшифровывается как Not a Number и получается в результате таких операций как 0/0.

2.8.6 В любой непонятной ситуации — ищите в поисковике

Если вдруг вы не знаете, что искать в хэлпе, или хэлпа попросту недостаточно, то ищите в поисковике!

Нет ничего постыдного в том, чтобы искать в Интернете решения проблем. Это абсолютно нормально. Используйте силу интернета во благо и да помогут вам Stackoverflow и бесчисленные R-туториалы!

Главное, помните: загуглить работающий ответ всегда недостаточно. Надо понять, как и почему он работает. Иначе что-то обязательно пойдет не так.

Кроме того, правильно загуглить проблему — не так уж и просто.

Итак, с векторами мы более-менее разобрались. Помните, что вектора — это один из краеугольных камней Вашей работы в R. Если Вы хорошо с ними разобрались, то дальше все будет довольно несложно. Тем не менее, вектора — это не все. Есть еще два важных типа данных: списки (list) и матрицы (matrix). Их можно рассматривать как своеобразное “расширение” векторов, каждый в свою сторону. Ну а списки и матрицы нужны чтобы понять основной тип данных в R — data.frame.

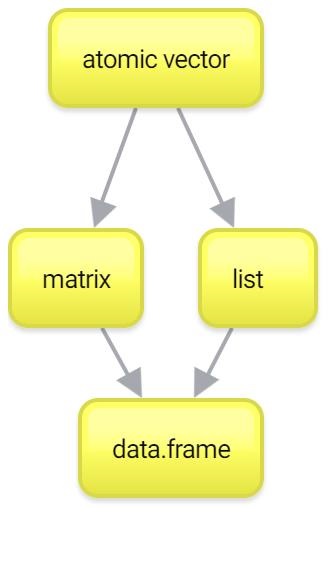
2.9 Матрицы (matrix)

Если вдруг Вас пугает это слово, то совершенно зря. Матрица — это всего лишь “двумерный” вектор: вектор, у которого есть не только длина, но и ширина. Создать матрицу можно с помощью функции matrix() из вектора, указав при этом количество строк и столбцов.

A <- matrix(1:20, nrow=5,ncol=4)
A
##      [,1] [,2] [,3] [,4]
## [1,]    1    6   11   16
## [2,]    2    7   12   17
## [3,]    3    8   13   18
## [4,]    4    9   14   19
## [5,]    5   10   15   20

Заметьте, значения вектора заполняются следующим образом: сначала заполняется первый столбик сверху вниз, потом второй сверху вниз и так до конца, т.е. заполнение значений матрицы идет в первую очередь по вертикали. Это довольно стандартный способ создания матриц, характерный не только для R.

Если мы знаем сколько значений в матрице и сколько мы хотим строк, то количество столбцов указывать необязательно:

A <- matrix(1:20, nrow=5)
A
##      [,1] [,2] [,3] [,4]
## [1,]    1    6   11   16
## [2,]    2    7   12   17
## [3,]    3    8   13   18
## [4,]    4    9   14   19
## [5,]    5   10   15   20

Все остальное так же как и с векторами: внутри находится данные только одного типа. Поскольку матрица — это уже двумерный массив, то у него имеется два индекса. Эти два индекса разделяются запятыми.

A[2,3]
## [1] 12
A[2:4, 1:3]
##      [,1] [,2] [,3]
## [1,]    2    7   12
## [2,]    3    8   13
## [3,]    4    9   14

Первый индекс — выбор строк, второй индекс — выбор колонок. Если же мы оставляем пустое поле вместо числа, то мы выбираем все строки/колонки в зависимости от того, оставили мы поле пустым до или после запятой:

A[,1:3]
##      [,1] [,2] [,3]
## [1,]    1    6   11
## [2,]    2    7   12
## [3,]    3    8   13
## [4,]    4    9   14
## [5,]    5   10   15
A[2:4,]
##      [,1] [,2] [,3] [,4]
## [1,]    2    7   12   17
## [2,]    3    8   13   18
## [3,]    4    9   14   19
A[,]
##      [,1] [,2] [,3] [,4]
## [1,]    1    6   11   16
## [2,]    2    7   12   17
## [3,]    3    8   13   18
## [4,]    4    9   14   19
## [5,]    5   10   15   20

Если мы выберем только одну колонку/строчку, то на выходе получим уже вектор, а не матрицу:

A[2,]
## [1]  2  7 12 17

Это называется “схлопыванием размерности.” Чтобы этого избежать, нужно поставить drop = FALSE после второй запятой внутри квадратных скобок.

A[2,, drop = FALSE]
##      [,1] [,2] [,3] [,4]
## [1,]    2    7   12   17

Для соединения двух или более матриц можно воспользоваться функциями rbind() и cbind() для соединения матриц по вертикали и по горизонтали соответственно.

rbind(A, A)
##       [,1] [,2] [,3] [,4]
##  [1,]    1    6   11   16
##  [2,]    2    7   12   17
##  [3,]    3    8   13   18
##  [4,]    4    9   14   19
##  [5,]    5   10   15   20
##  [6,]    1    6   11   16
##  [7,]    2    7   12   17
##  [8,]    3    8   13   18
##  [9,]    4    9   14   19
## [10,]    5   10   15   20
cbind(A, A)
##      [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
## [1,]    1    6   11   16    1    6   11   16
## [2,]    2    7   12   17    2    7   12   17
## [3,]    3    8   13   18    3    8   13   18
## [4,]    4    9   14   19    4    9   14   19
## [5,]    5   10   15   20    5   10   15   20

В принципе, это все, что нам нужно знать о матрицах. Матрицы используются в R довольно редко, особенно по сравнению, например, с MATLAB. Но вот индексировать матрицы хорошо бы уметь: это понадобится в работе с датафреймами.

То, что матрица - это просто двумерный вектор, не является метафорой: в R матрица - это по сути своей вектор с дополнительными атрибутами dim и dimnames. Атрибуты — это неотъемлемые свойства объектов, для всех объектов есть обязательные атрибуты типа и длины и могут быть любые необязательные атрибуты. Можно задавать свои атрибуты или удалять уже присвоенные: удаление атрибута dim у матрицы превратит ее в обычный вектор. Про атрибуты подробнее можно почитать здесь или на стр. 99–101 книги “R in a Nutshell” (Adler 2010).

2.10 Списки (list)

Теперь представим себе вектор без ограничения на одинаковые данные внутри. И получим список!

simple_list <- list(42, "Пам пам", TRUE)
simple_list
## [[1]]
## [1] 42
## 
## [[2]]
## [1] "Пам пам"
## 
## [[3]]
## [1] TRUE

А это значит, что там могут содержаться самые разные данные, в том числе и другие списки и векторы!

complex_list <- list(c("Wow", "this", "list", "is", "so", "big"), "16", simple_list)
complex_list
## [[1]]
## [1] "Wow"  "this" "list" "is"   "so"   "big" 
## 
## [[2]]
## [1] "16"
## 
## [[3]]
## [[3]][[1]]
## [1] 42
## 
## [[3]][[2]]
## [1] "Пам пам"
## 
## [[3]][[3]]
## [1] TRUE

Если у нас сложный список, то есть очень классная функция, чтобы посмотреть, как он устроен, под названием str():

str(complex_list)
## List of 3
##  $ : chr [1:6] "Wow" "this" "list" "is" ...
##  $ : chr "16"
##  $ :List of 3
##   ..$ : num 42
##   ..$ : chr "Пам пам"
##   ..$ : logi TRUE

Как и в случае с векторами мы можем давать имена элементам списка:

named_list <- list(age = 24, phd_student = T, language = "Russian")
named_list
## $age
## [1] 24
## 
## $phd_student
## [1] FALSE
## 
## $language
## [1] "Russian"

К списку можно обращаться как с помощью индексов, так и по именам. Начнем с последнего:

named_list$age
## [1] 24

А вот с индексами сложнее, и в этом очень легко запутаться. Давайте попробуем сделать так, как мы делали это раньше:

named_list[1]
## $age
## [1] 24

Мы, по сути, получили элемент списка - просто как часть списка, т.е. как список длиной один:

class(named_list)
## [1] "list"
class(named_list[1])
## [1] "list"

А вот чтобы добраться до самого элемента списка (и сделать с ним что-то хорошее) нам нужна не одна, а две квадратных скобочки:

named_list[[1]]
## [1] 24
class(named_list[[1]])
## [1] "numeric"

Как и в случае с вектором, к элементу списка можно обращаться по имени.

named_list[['age']]
## [1] 24

Хотя последнее — практически то же самое, что и использование знака $.

Списки довольно часто используются в R, но реже, чем в Python. Со многими объектами в R, такими как результаты статистических тестов, объекты ggplot и т.д. удобно работать именно как со списками — к ним все вышеописанное применимо. Кроме того, некоторые данные мы изначально получаем в виде древообразной структуры — хочешь не хочешь, а придется работать с этим как со списком. Особенно это характерно для данных, выкачанных из веб-страниц (HTML страницы, XML данные) или полученных с помощью API различных веб-сайтов (например, в формате JSON). Но обычно после этого стоит как можно скорее превратить список в датафрейм.

2.11 Датафрейм

Итак, мы перешли к самому главному. Самому-самому. Датафреймы (data.frames). Более того, сейчас станет понятно, зачем нам нужно было разбираться со всеми предыдущими темами.

Без векторов мы не смогли бы разобраться с матрицами и списками. А без последних мы не сможем понять, что такое датафрейм.

name <- c("Ivan", "Eugeny", "Lena", "Misha", "Sasha") 
age <- c(26, 34, 23, 27, 26) 
student <- c(FALSE, FALSE, TRUE, TRUE, TRUE) 
df = data.frame(name, age, student)  
df
str(df)
## 'data.frame':    5 obs. of  3 variables:
##  $ name   : chr  "Ivan" "Eugeny" "Lena" "Misha" ...
##  $ age    : num  26 34 23 27 26
##  $ student: logi  FALSE FALSE TRUE TRUE TRUE

Вообще, очень похоже на список, не правда ли? Так и есть, датафрейм — это что-то вроде проименованного списка, каждый элемент которого является atomic вектором фиксированной длины. Скорее всего, список Вы представляли “горизонтально.” Если это так, то теперь “переверните” его у себя в голове. Так, чтоб названия векторов оказались сверху, а колонки стали столбцами. Поскольку длина всех этих векторов равна (обязательное условие!), то данные представляют собой табличку, похожую на матрицу. Но в отличие от матрицы, разные столбцы могут имет разные типы данных: первая колонка — character, вторая колонка — numeric, третья колонка — logical. Тем не менее, обращаться с датафреймом можно и как с проименованным списком, и как с матрицей:

df$age[2:3]
## [1] 34 23

Здесь мы сначала вытащили колонку age с помощью оператора $. Результатом этой операции является числовой вектор, из которого мы вытащили кусок, выбрав индексы 2 и 3.

Используя оператор $ и присваивание можно создавать новые колонки датафрейма:

df$lovesR <- TRUE #правило recycling - узнали? 
df

Ну а можно просто обращаться с помощью двух индексов через запятую, как мы это делали с матрицей:

df[3:5, 2:3]

Как и с матрицами, первый индекс означает строчки, а второй — столбцы.

А еще можно использовать названия колонок внутри квадратных скобок:

df[1:2,"age"]
## [1] 26 34

И здесь перед нами открываются невообразимые возможности! Узнаем, любят ли R те, кто моложе среднего возраста в группе:

df[df$age < mean(df$age), 4]
## [1] TRUE TRUE TRUE TRUE

Эту же задачу можно выполнить другими способами:

df$lovesR[df$age < mean(df$age)]
## [1] TRUE TRUE TRUE TRUE
df[df$age < mean(df$age), 'lovesR']
## [1] TRUE TRUE TRUE TRUE

В большинстве случаев подходят сразу несколько способов — тем не менее, стоит овладеть ими всеми.

Датафреймы удобно просматривать в RStudio. Для это нужно написать команду View(df) или же просто нажать на названии нужной переменной из списка вверху справа (там где Environment). Тогда увидите табличку, очень похожую на Excel и тому подобные программы для работы с таблицами. Там же есть и всякие возможности для фильтрации, сортировки и поиска… Но, конечно, интереснее все эти вещи делать руками, т.е. с помощью написания кода.

На этом пора заканчивать с введением и приступать к реальным данным.

Ссылки на литературу

Adler, Joseph. 2010. R in a Nutshell: A Desktop Quick Reference. " O’Reilly Media, Inc.".
Baesens, Bart, Veronique Van Vlasselaer, and Wouter Verbeke. 2015. Fraud Analytics Using Descriptive, Predictive, and Social Network Techniques: A Guide to Data Science for Fraud Detection. John Wiley & Sons.
Brooks, Harvey, and Chester L Cooper. 2013. Science for Public Policy. Elsevier.
Hansjörg, Neth. 2019. Data Science for Psychologists. self published.
Provost, Foster, and Tom Fawcett. 2013. Data Science for Business: What You Need to Know about Data Mining and Data-Analytic Thinking. O’Reilly Media, Inc.
R Core Team. 2019. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.
Thomas, Niclas, and Laura Pallett. 2019. Data Science for Immunologists. CreateSpace Independent Publishing Platform.
Wickham, Hadley, and Garrett Grolemund. 2016. R for Data Science: Import, Tidy, Transform, Visualize, and Model Data. O’Reilly Media, Inc.

  1. Есть еще оператор ->, который позволяет присваивать значения слева направо, но так делать не рекомендуется, хотя это бывает довольно удобным.↩︎

  2. Еще иногда используются большие буквы SomeVariable, но это плохо читается, а иногда — точка, но это тоже не рекомендуется.↩︎

  3. Комплексные числа в R пишутся так: complexnumber <- 2+2i. i здесь - это та самая мнимая единица, которая является квадратным корнем из -1.↩︎

  4. Кроме описанных пяти типов данных (integer, double, complex, character и logical) есть еще и шестой — это raw, сырая последовательность байтов, но нам она не понадобится.↩︎