3. Байесовский доверительный интервал

1.1

Чтобы не скучать, посчитайте 95% доверительный интервал для среднего значения уровня кислотности (ph) в датасете про мочу. Укажите нижнюю границу доверительного интервала (mean - ci) (два знака после запятой).

1.2 Бутстрэп

Если нужны какие-то более изощренные статистики, то можно использовать бустрэп.

library(bootstrap)

set.seed(42)
boot_mean <- bootstrap(urine$ph, nboot = 1000, theta = mean)

1.3 Доверительный интервал и биномиальные данные

Сначала данные:

• количество “не” в 311 рассказов А. Чехова
• число слов в каждом рассказе

chekhov <- read_csv("https://raw.githubusercontent.com/agricolamz/2019_BayesDan_winter/master/datasets/chekhov.csv")

chekhov %>% 
  mutate(trunc_titles = str_trunc(titles, 25, side = "right"),
         average = n/n_words) ->
  chekhov

Распространение логики доверительного интервала на биномиальные данные называется интервал Вальда:

\[\bar{x} = \theta; \sigma = \sqrt{\frac{\theta\times(1-\theta)}{n}}\]

Тогда интервал Вальда:

\[\theta \pm z\times\sqrt{\frac{\theta\times(1-\theta)} {n}}\]

Есть только одна проблема: работает он плохо. Его аналоги перечислены в других работах:

• assymptotic method with continuity correction
• Wilson score
• Wilson Score method with continuity correction
• Jeffreys interval
• Clopper–Pearson interval (default in R binom.test())
• Agresti–Coull interval
• … см. пакет binom

chekhov %>% 
  slice(1:30) %>% 
  group_by(titles) %>% 
  mutate(low_ci = mosaic::binom.test(x = n, n = n_words, ci.method = "Clopper-Pearson")$conf.int[1],
         up_ci = mosaic::binom.test(x = n, n = n_words, ci.method = "Clopper-Pearson")$conf.int[2]) %>%
  ggplot(aes(trunc_titles, average))+
  geom_point()+
  geom_pointrange(aes(ymin = low_ci, ymax = up_ci))+
  coord_flip()+
  labs(title = 'Среднее и 95% CI употребления "не" в рассказах А. Чехова',
       x = "", y = "")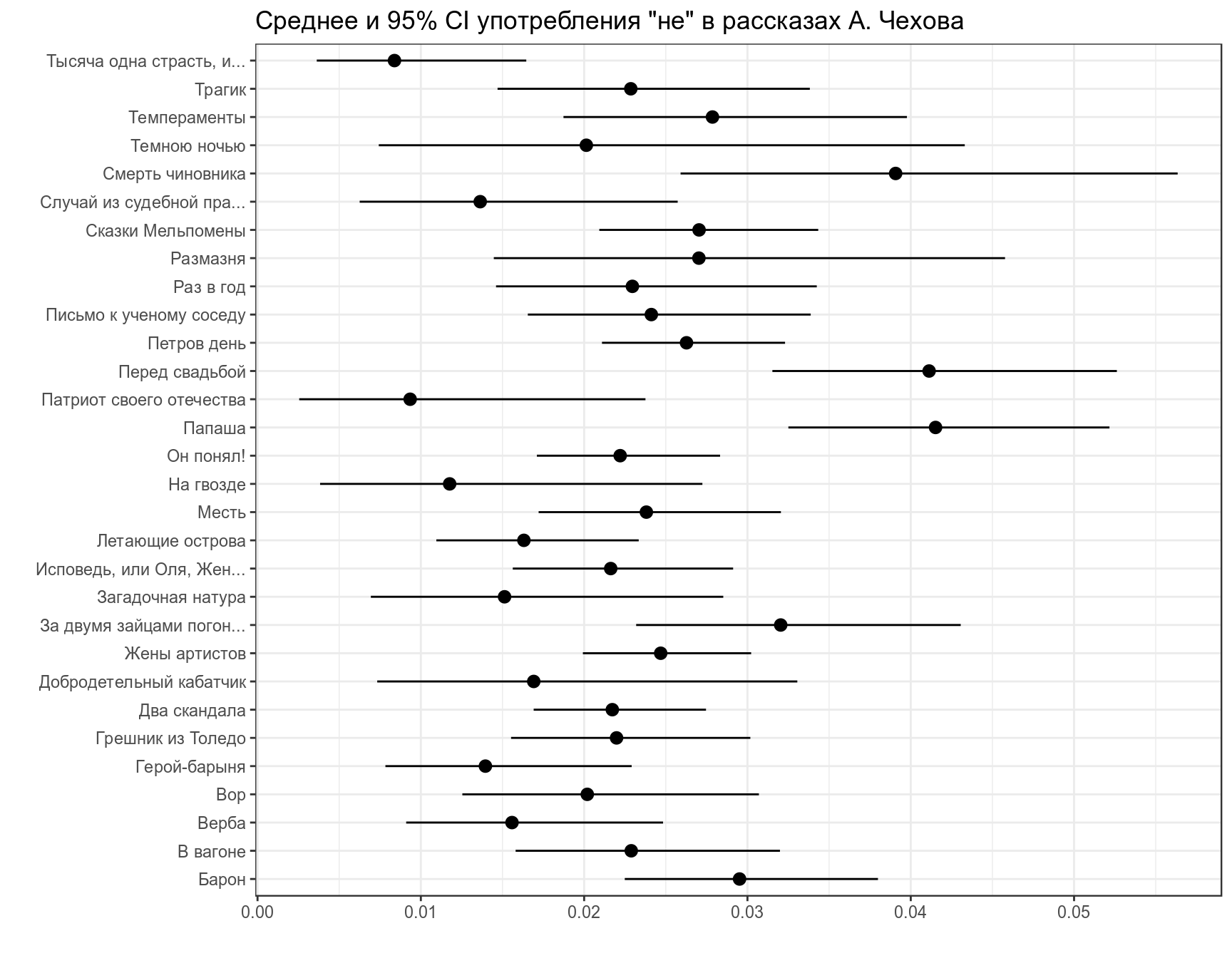

В базовом пакете функция binom.test() не позволяет выбирать тип доверительного интервала. ci.method = "Clopper-Pearson" возможна, если включить библиотеку mosaic.

1.4

В базе данных Phoible, в которой собраны фонологические инвентари в языках мира. В датасет записано три переменных:

• language — язык;
• consonants — количество согласных;
• phonemes — количество фонем.

Посчитайте долю, которая составляет согласные от всего фонологического набора каждого языка и доверительный интервал для него (ci.method = "Clopper-Pearson"). Полученные интервалы округлите до 3 знаков после запятой, а в ответ укажите название языка на букву N с интервалом равный 0.514.

2.1 Симметричный интервал (equal-tailed interval): медиана и квантили

Байесовский доверительный \(k\)-% интервал (по-английски credible interval) — это интервал \([\frac{k}{2}, 1-\frac{k}{2}]\) от апостериорного распределения. Давайте проапдейтим данные рассказов Чехова при помощи априорного распределения с параметрами (\(\alpha = 5.283022\), \(\beta = 231.6328\)), а дальше можем использовать функцию qbeta(), чтобы получить интервал, в котором находятся центральные \(k\)%.

chekhov %>% 
  slice(1:30) %>%
  group_by(trunc_titles) %>% 
  mutate(beta_prior = n_words-n,
         alpha_post = n + 5.283022,
         beta_post = beta_prior + 231.6328,
         median_post = qbeta(.5, alpha_post, beta_post),
         eq_t_int_l = qbeta(.025, alpha_post, beta_post),
         eq_t_int_h = qbeta(.975, alpha_post, beta_post),
         low_ci = mosaic::binom.test(x = n, n = n_words)$conf.int[1],
         up_ci = mosaic::binom.test(x = n, n = n_words)$conf.int[2]) %>% 
  ggplot(aes(x= trunc_titles))+
  geom_pointrange(aes(y = average, ymin = low_ci, ymax = up_ci), color = "royalblue")+
  geom_pointrange(aes(y = median_post, ymin = eq_t_int_l, ymax = eq_t_int_h), color = "tomato", position = position_nudge(x = -0.35))+
  coord_flip()+
  labs(title = 'Доверительные интервалы употребления "не" в рассказах А. Чехова',
       x = "", y = "",
       caption = "красные --- фриквентистский; синий --- байесовский eq-t")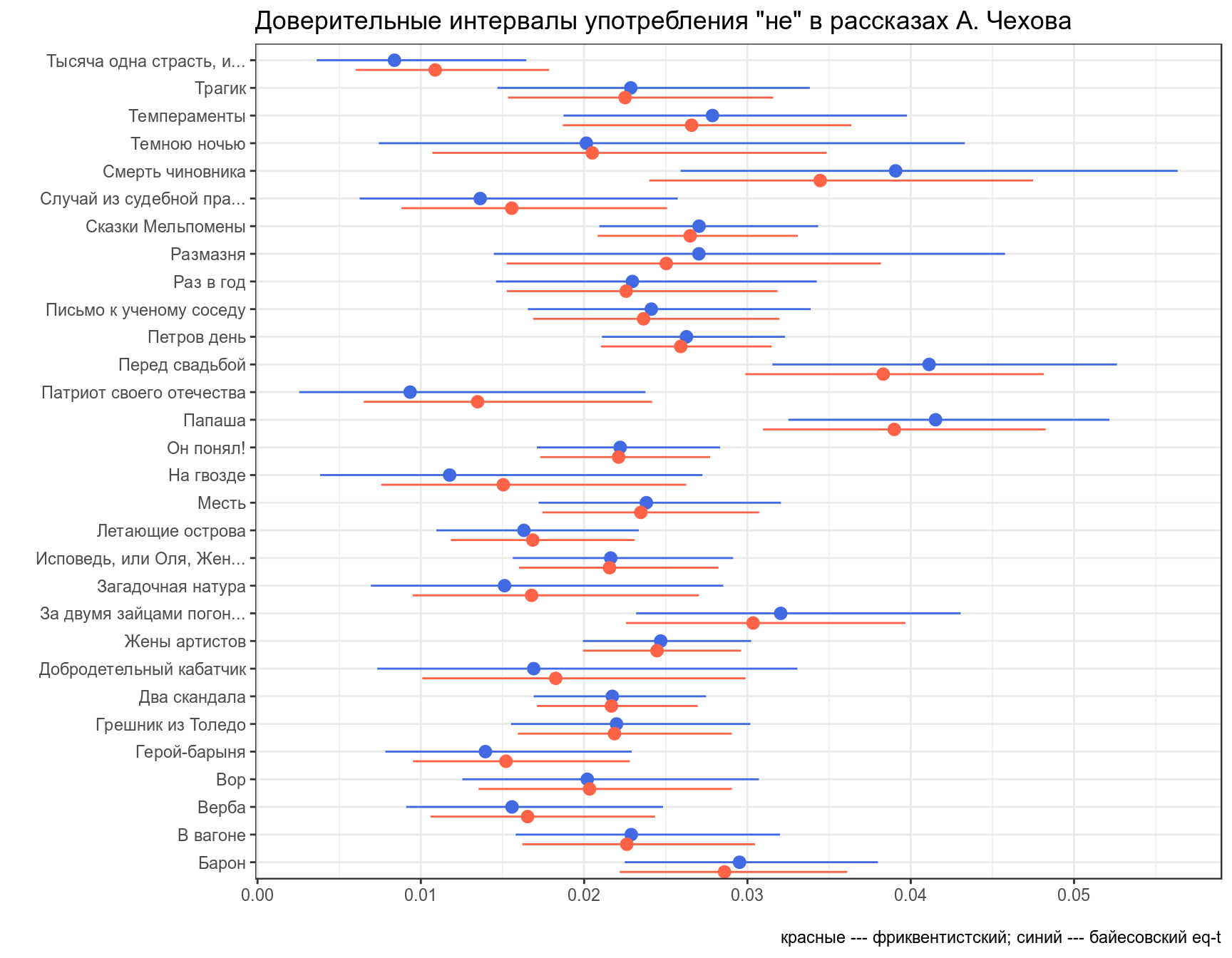

2.2 Интервал максимальной (апостериорной) плотности (Highest (posterior) density interval): мода и HDI

chekhov %>% 
  slice(1:30) %>%
  group_by(trunc_titles) %>% 
  mutate(beta_prior = n_words-n,
         alpha_post = n + 5.283022,
         beta_post = beta_prior + 231.6328,
         median_post = qbeta(.5, alpha_post, beta_post),
         moda_post = (alpha_post-1)/(alpha_post+beta_post-2),
         hdi_int_l = hdi(qbeta, shape1 = alpha_post, shape2 = beta_post, credMass = 0.95)[1],
         hdi_int_h = hdi(qbeta, shape1 = alpha_post, shape2 = beta_post, credMass = 0.95)[2],
         eq_t_int_l = qbeta(.025, alpha_post, beta_post),
         eq_t_int_h = qbeta(.975, alpha_post, beta_post),
         low_ci = mosaic::binom.test(x = n, n = n_words)$conf.int[1],
         up_ci = mosaic::binom.test(x = n, n = n_words)$conf.int[2]) %>% 
  ggplot(aes(x= trunc_titles))+
  geom_pointrange(aes(y = average, ymin = low_ci, ymax = up_ci), color = "royalblue", position = position_nudge(x = 0.25))+
  geom_pointrange(aes(y = median_post, ymin = eq_t_int_l, ymax = eq_t_int_h), color = "tomato")+
  geom_pointrange(aes(y = moda_post, ymin = hdi_int_l, ymax = hdi_int_h), color = "palegreen3", position = position_nudge(x = -0.25))+
  coord_flip()+
  labs(title = 'Доверительные интервалы употребления "не" в рассказах А. Чехова',
       x = "", y = "",
       caption = "красные --- фриквентистский; синий --- байесовский eq-t; зеленый --- байсовский hdi")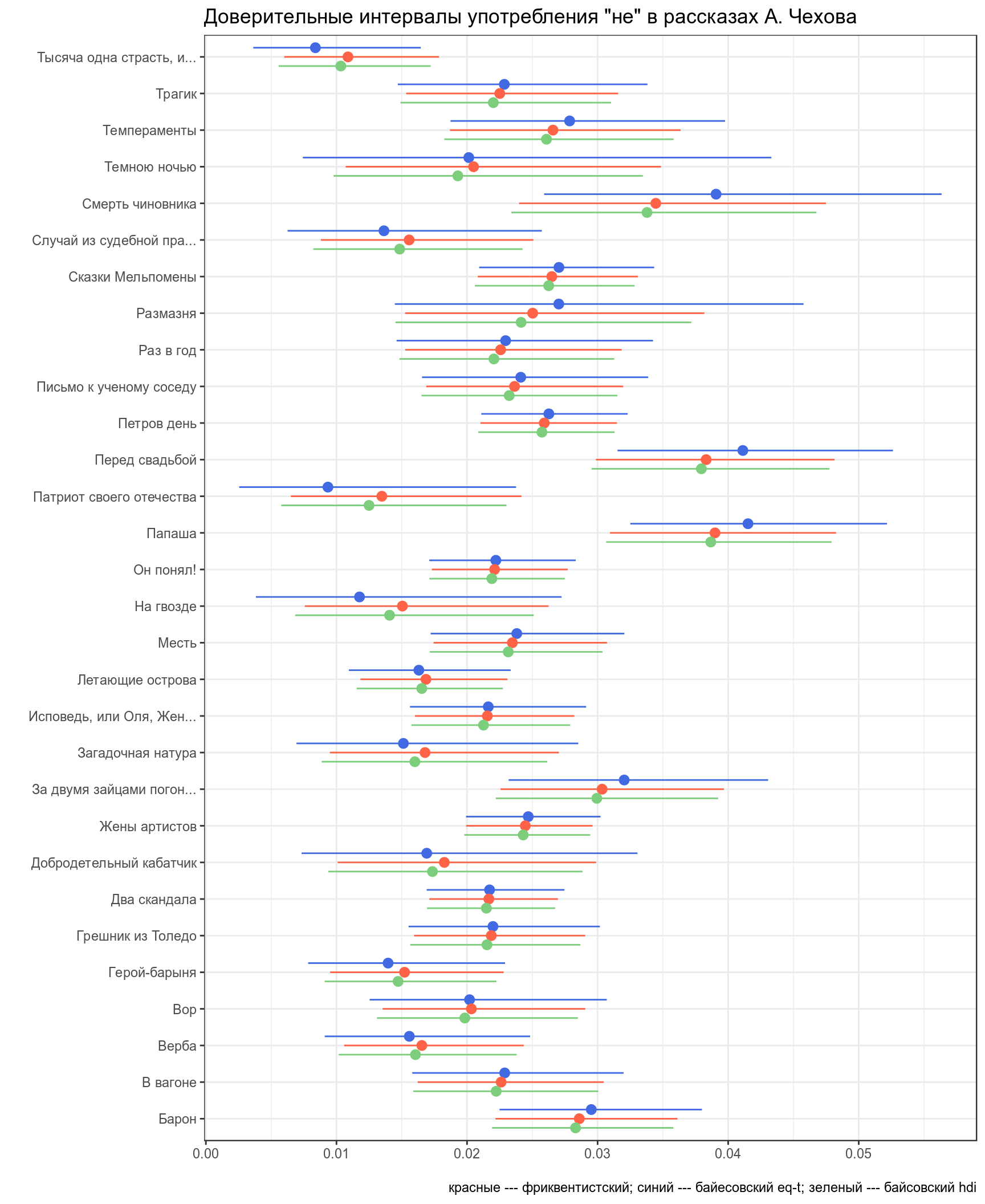

В качестве аргумента в пользу HDI всегда приводят вот такое распределение:

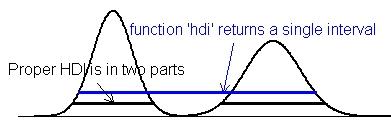
2.4

В базе данных Phoible, в которой собраны фонологические инвентари в языках мира. В датасет записано три переменных:

• language — язык;
• consonants — количество согласных;
• phonemes — количество фонем.

Посчитайте медиану и 80% симметричный интервал, которую составляет согласные от всего фонологического набора каждого языка, используя априорное бета распределение с параметрами α = 9.300246 и β = 4.4545. В ответе укажите язык, у которого интервал равен 0.083.

2.5

В базе данных Phoible, в которой собраны фонологические инвентари в языках мира. В датасет записано три переменных:

• language — язык;
• consonants — количество согласных;
• phonemes — количество фонем.

Посчитайте моду и 80% интервал максимальной апостериорной плотности, которую составляет согласные от всего фонологического набора каждого языка, используя априорное бета распределение с параметрами α = 9.300246 и β = 4.4545. В ответе укажите язык, у которого интервал равен 0.091.

phoible <- read_csv("https://raw.githubusercontent.com/agricolamz/2019_BayesDan_winter/master/datasets/phoible_n_consonants.csv") 

phoible %>%
  group_by(language) %>% 
  rowwise() %>% # это нужно, так как авторы HDInterval не векторизовали hdi
  mutate(...) %>%