4. Эмпирическая байесовская оценка

1. Эмпирическая байесовская оценка (Empirical Bayes Estimation)

Если наши данные представляют собой группировки независимых наблюдений, в которых мы предполагаем сходное значение оцениваемого параметра θ (доля не в куче рассказов Чехова, количество согласных в языках мира и т. д.), можно применять эмпирическую байесовскую оценку априорного распределения.

Эмпирическая байесовская оценка — один из байесовских методов, в рамках которого:

• производят оценку априорного распределения вероятностей на основании имеющихся данных
• используют полученное априорное распределение для получение апостериорной оценки для каждого наблюдения

chekhov <- read_csv("https://raw.githubusercontent.com/agricolamz/2019_BayesDan_winter/master/datasets/chekhov.csv")
chekhov %>% 
  mutate(trunc_titles = str_trunc(titles, 25, side = "right"),
         average = n/n_words) ->
  chekhov
head(chekhov)

• 311 рассказов А. Чехова
• число слов в каждом рассказе

Наши данные:

chekhov %>% 
  ggplot(aes(average)) +
  geom_histogram(fill = "lightblue")+
  geom_density(color = "red")+
  theme_bw()+
  labs(title = 'Частотность слова "не" на основе 305 рассказов А. Чехова')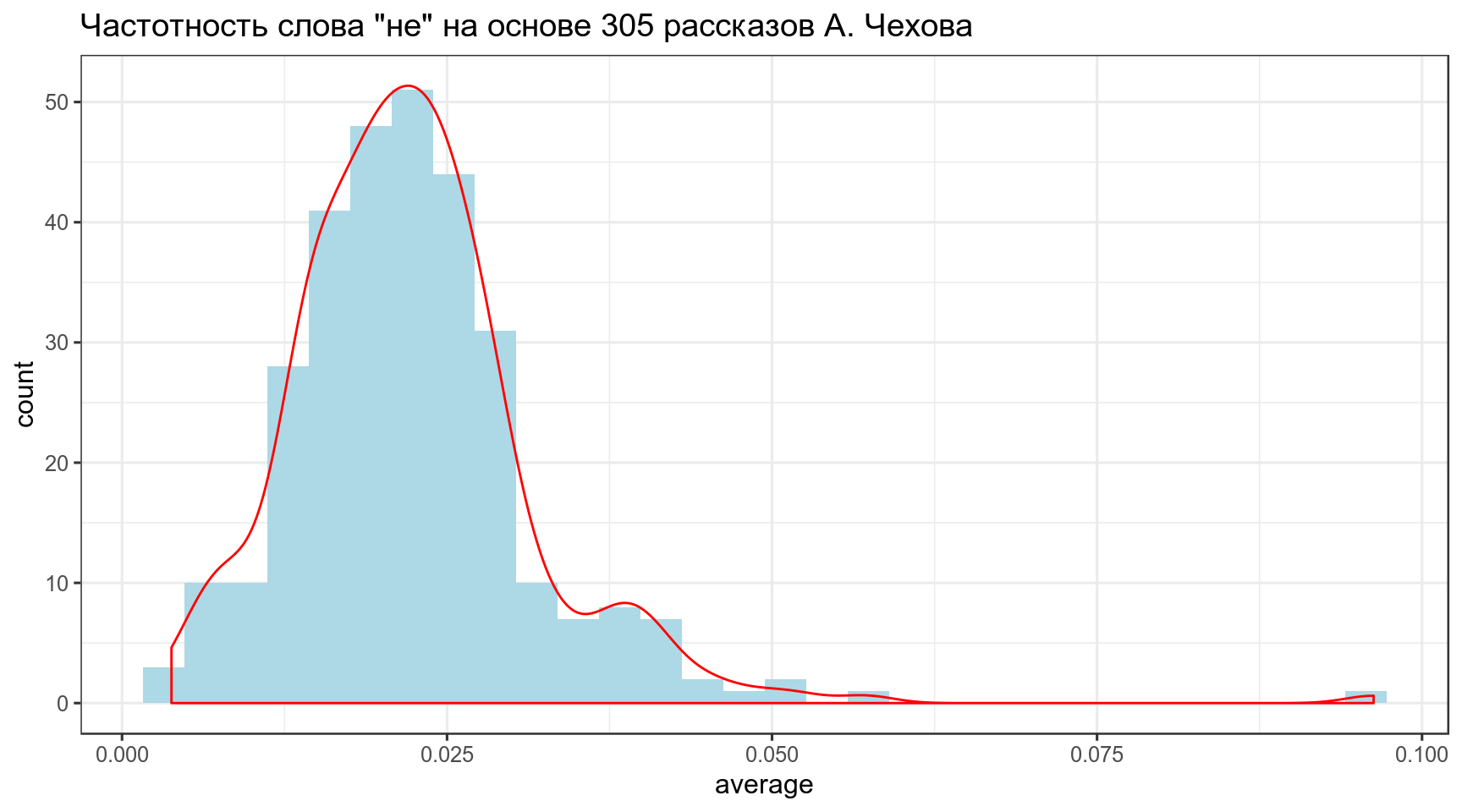

В данном случае, данные можно подогнать под бета распределение \(Χ \sim Beta(α_0, β_0)\) (это далеко не всегда так). Подгонку можно осуществлять множеством разных функций, но я воспользуюсь следующей системой уравнений:

\[\mu = \frac{\alpha}{\alpha+\beta}\] \[\sigma = \frac{\alpha\times\beta}{(\alpha+\beta)^2\times(\alpha+\beta+1)}\]

Из этой системы можно выразить \(\alpha\) и \(\beta\):

\[\alpha = \left(\frac{1-\mu}{\sigma^2} - \frac{1}{\mu}\right)\times \mu^2\] \[\beta = \alpha\times\left(\frac{1}{\mu} - 1\right)\]

mu <- mean(chekhov$average)
var <- var(chekhov$average)
alpha0 <- ((1 - mu) / var - 1 / mu) * mu ^ 2
beta0 <- alpha0 * (1 / mu - 1)
alpha0

[1] 5.283022

beta0

[1] 231.6328

Посмотрим, насколько хорошо, получившееся распределение подходит к нашим данным:

x <- seq(0, 0.1, length = 1000)
estimation <- data_frame(
  x = x,
  density = c(dbeta(x, shape1 = alpha0, shape2 = beta0)))

chekhov %>% 
  ggplot(aes(average)) +
  geom_density(fill = "lightblue")+
  geom_line(data = estimation, aes(x, density), color = 'red')+
  theme_bw()+
  labs(title = 'Частотность слова "не" на основе 305 рассказов А. Чехова',
       subtitle = "черной линией показано бета распределение с α = 5.283022 и β = 231.6328")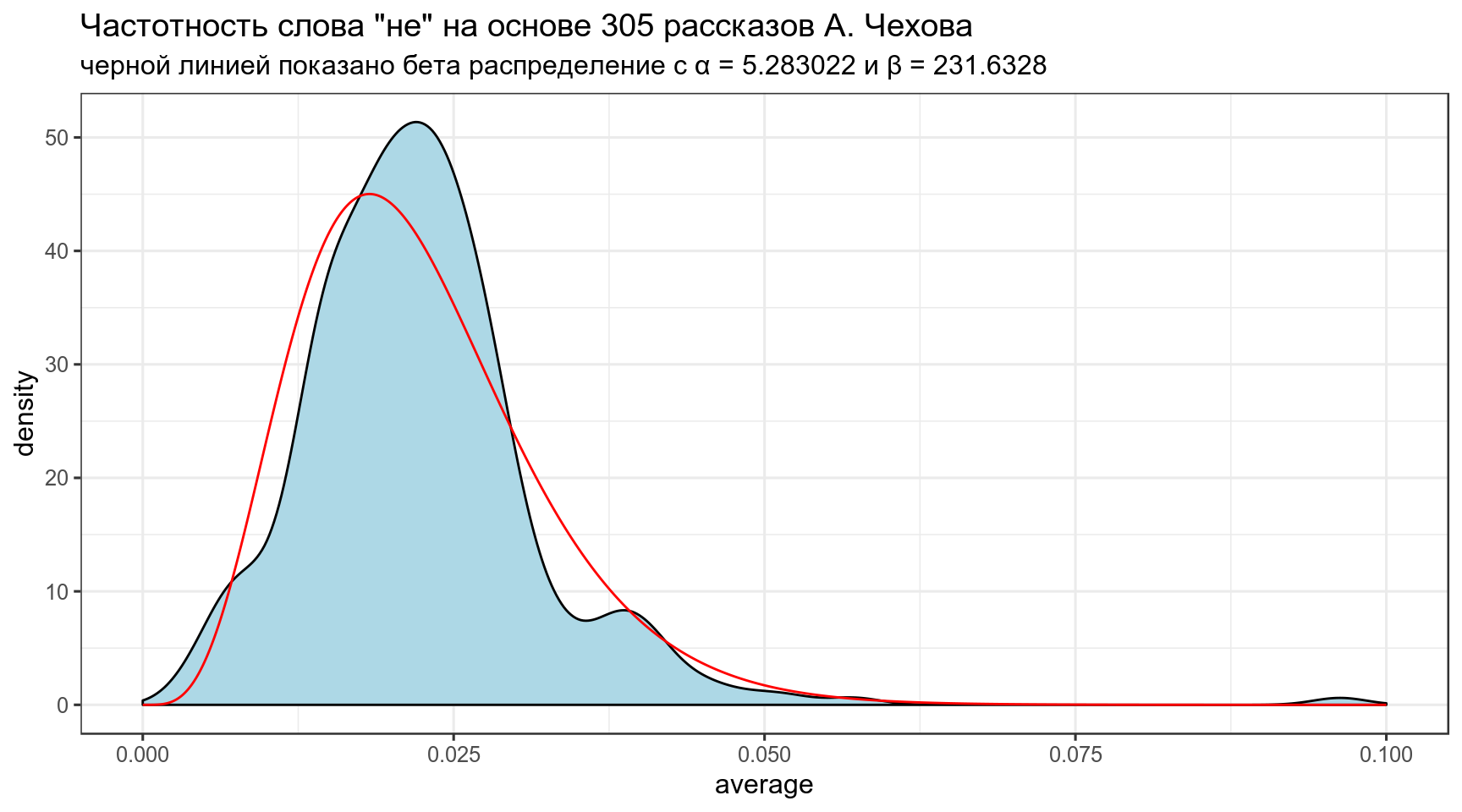

Полученное распределение можно использовать как априорное распределение для апдейта значений из каждого рассказа. Этот трюк и называется эмпирическая байесовская оценка.