6. Марковские цепи
Г. Мороз
1. Рандомизаторы
1.1 Простой случай
В нашем курсе мы обсуждали несколько рандомизаторов (rnorm(), rbeta() и так далее). Но вернемся к более простому случаю. Сделаем одну выборку из множества, содержащего три элемента:
[1] 7 5 6По умолчанию он выдает множество равное количеству объектов в векторе.
[1] 7Error in sample.int(length(x), size, replace, prob): cannot take a sample larger than the population when 'replace = FALSE'[1] 6 7 7 7Можно задавать вероятности, с которыми рандомизатор вынимает то или иное значение (по умолчанию все исходы равновероятны):
.
5 6 7
0.3253 0.3338 0.3409 .
5 6 7
0.1023 0.2953 0.6024 Записи идентичны:
[1] 9 10 3 4 5 2 6 1 7 8 [1] 4 3 2 8 7 9 1 6 5 10Чтобы фиксировать рандомизатор следует использовать set.seed(). Посмотрите прекрасную работу Бена Мура на тему того, какие кто использует сиды на GitHub.
Иногда хочется, чтобы рандомизатор был одинаковый в R и Python, зачем и как это делать читайте в работе Гертьяна ван ден Бург: блог, гитхаб.
1.2 Сэмплирование из датафрейма
2. Марковские цепи
Марковский процесс
- конечное количество состояний
- вероятность переходов из одного состояния в другое
Славная визуализация (спасибо за ссылку Марине Дубовой)
Возьмем наш датасет с погодой и отфильтруем только Сан Диего:
read_csv("https://raw.githubusercontent.com/agricolamz/2019_BayesDan_winter/master/datasets/weather.csv") %>%
select(city, date, events) %>%
filter(city == "San Diego") ->
weather
weather %>%
ggplot(aes(date, events))+
geom_point()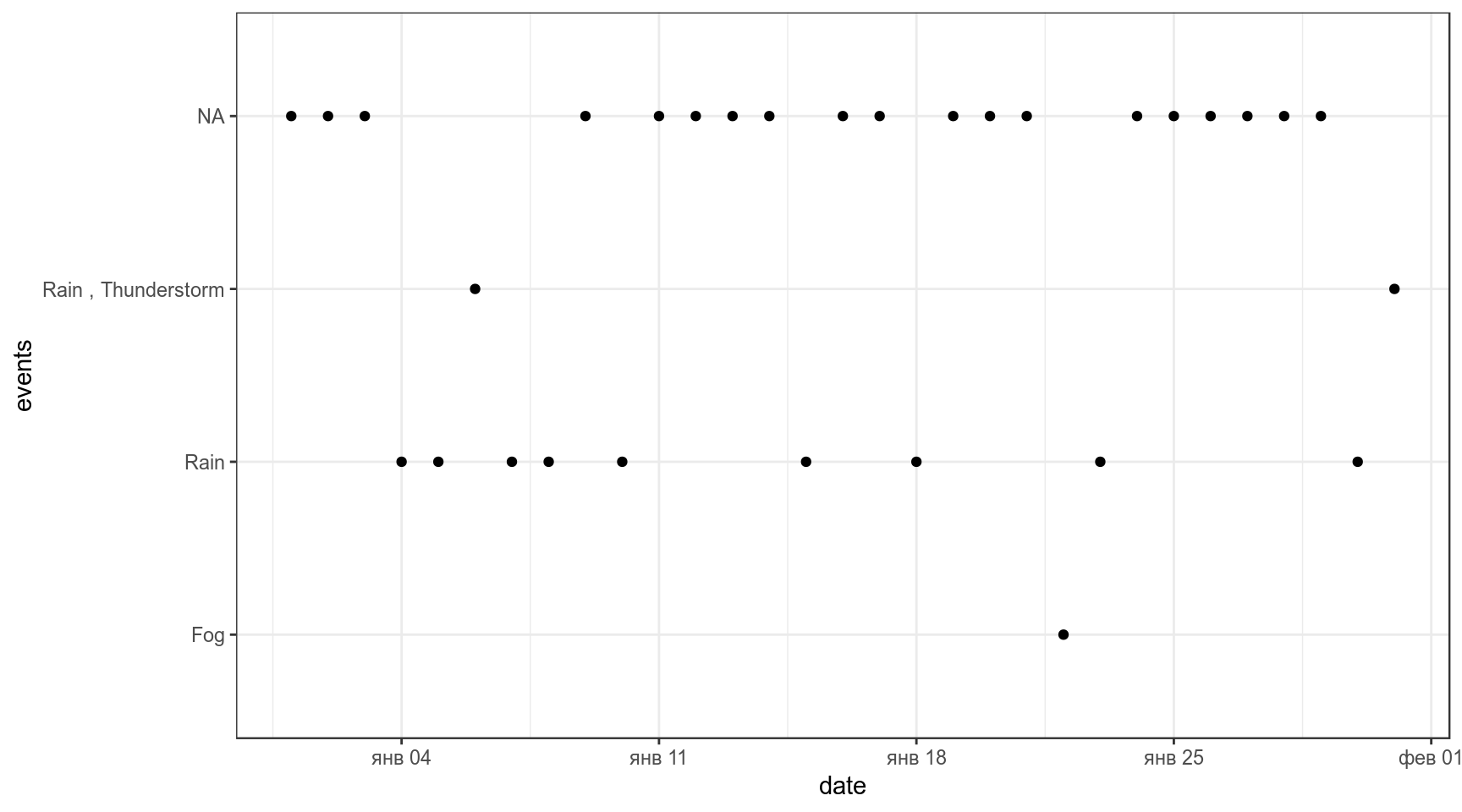
Давайте считать, что NA — это солнце.
weather %>%
mutate(events = ifelse(is.na(events), "Sun", events)) ->
weather
weather%>%
ggplot(aes(date, events))+
geom_point()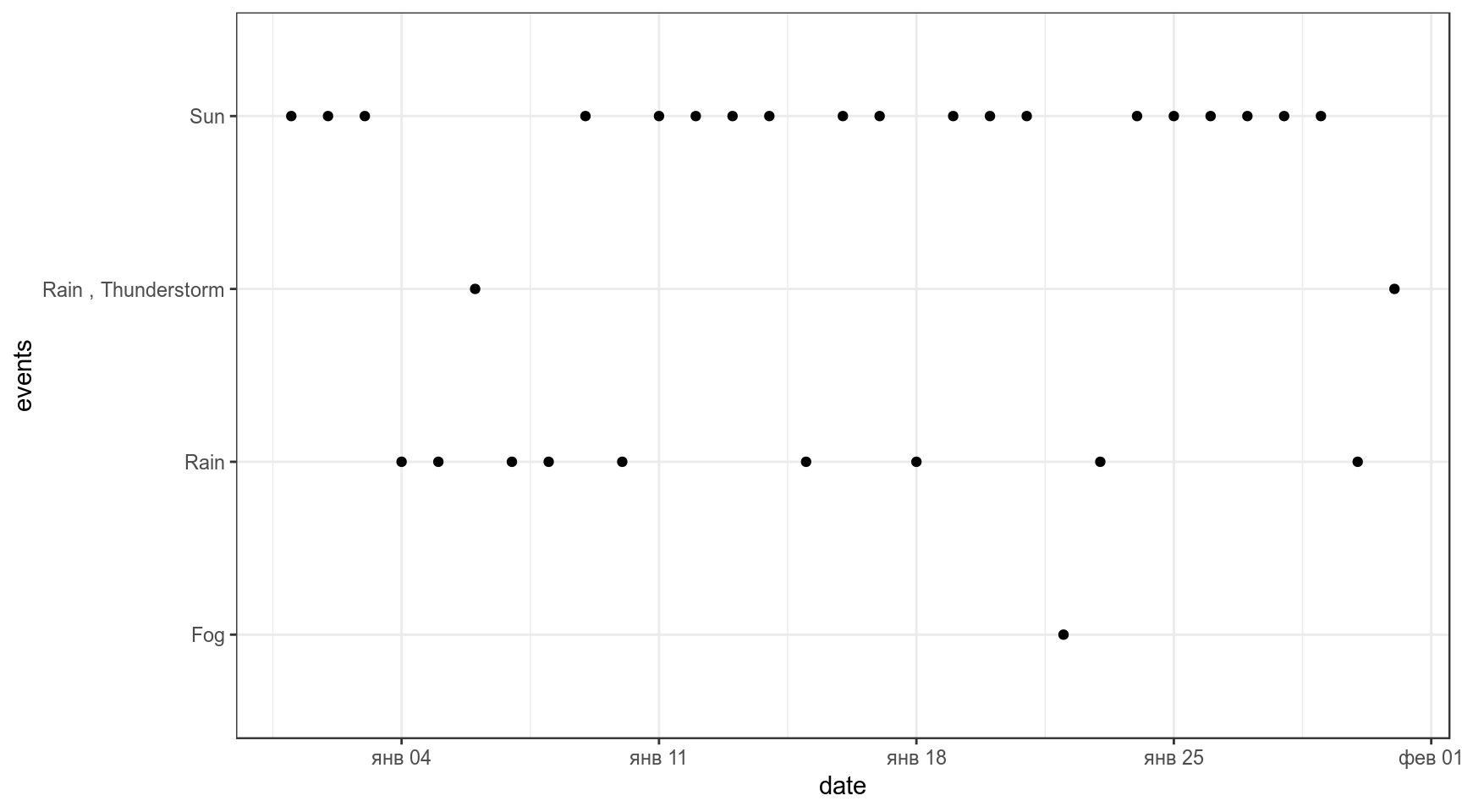
Визуализируем частоты разных погодных событий в Сан Диего:
weather %>%
count(events) %>%
mutate(events = reorder(factor(events), n)) %>%
ggplot(aes(events, n))+
geom_col(fill = "lightblue")+
coord_flip()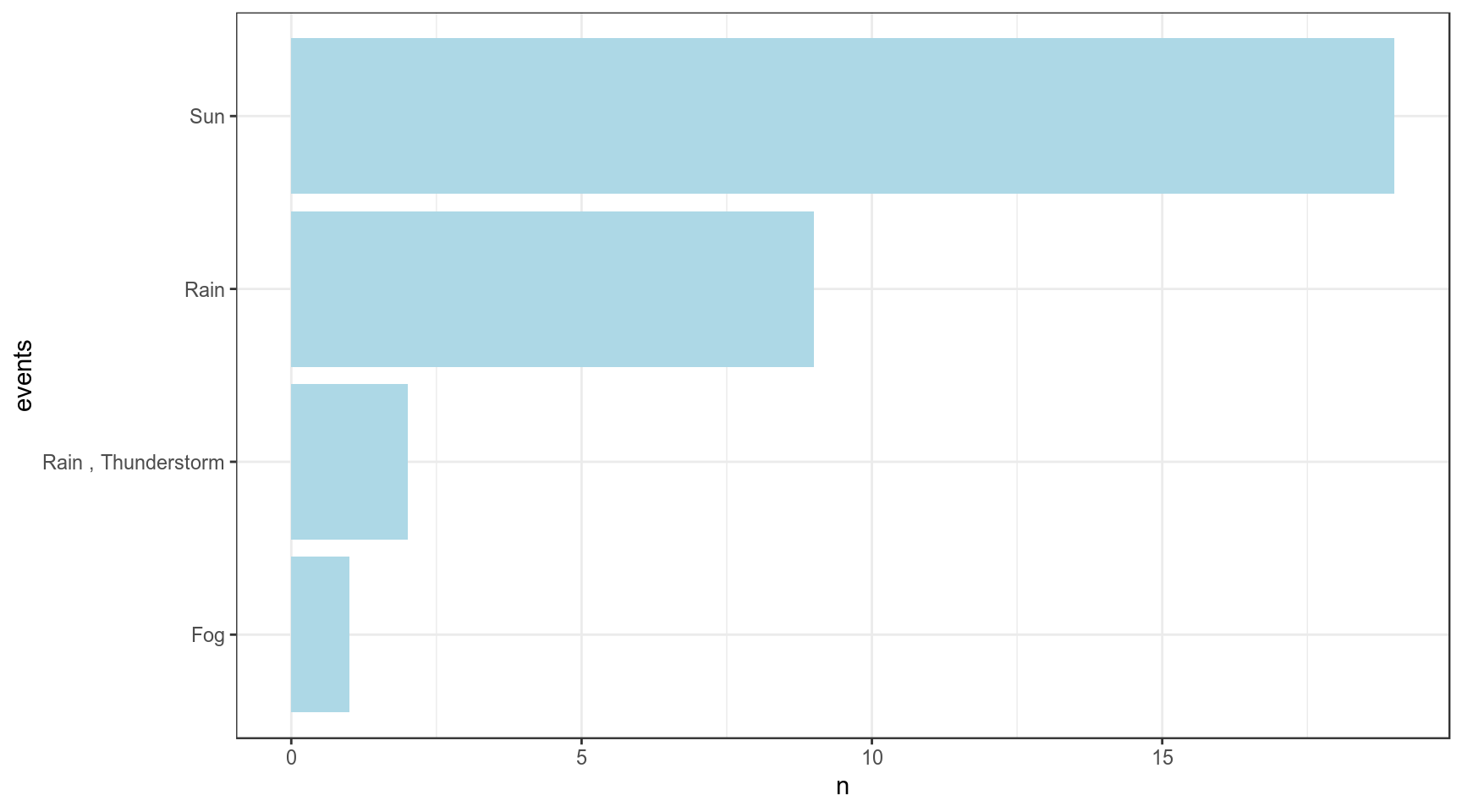
Визуализируем матрицу последовательных переходов разных погодных событий:
data_frame(bigramma_1 = weather$events,
bigramma_2 = lead(weather$events, 1)) %>%
table() %>%
prop.table() %>%
as.data.frame() %>%
ggplot(aes(bigramma_1, bigramma_2, size = Freq, fill = Freq))+
geom_raster()+
geom_point()+
scale_fill_gradient(low="grey95", high="red")+
labs(title = 'Матрица переходов погодных событий в Сан Диего в январе')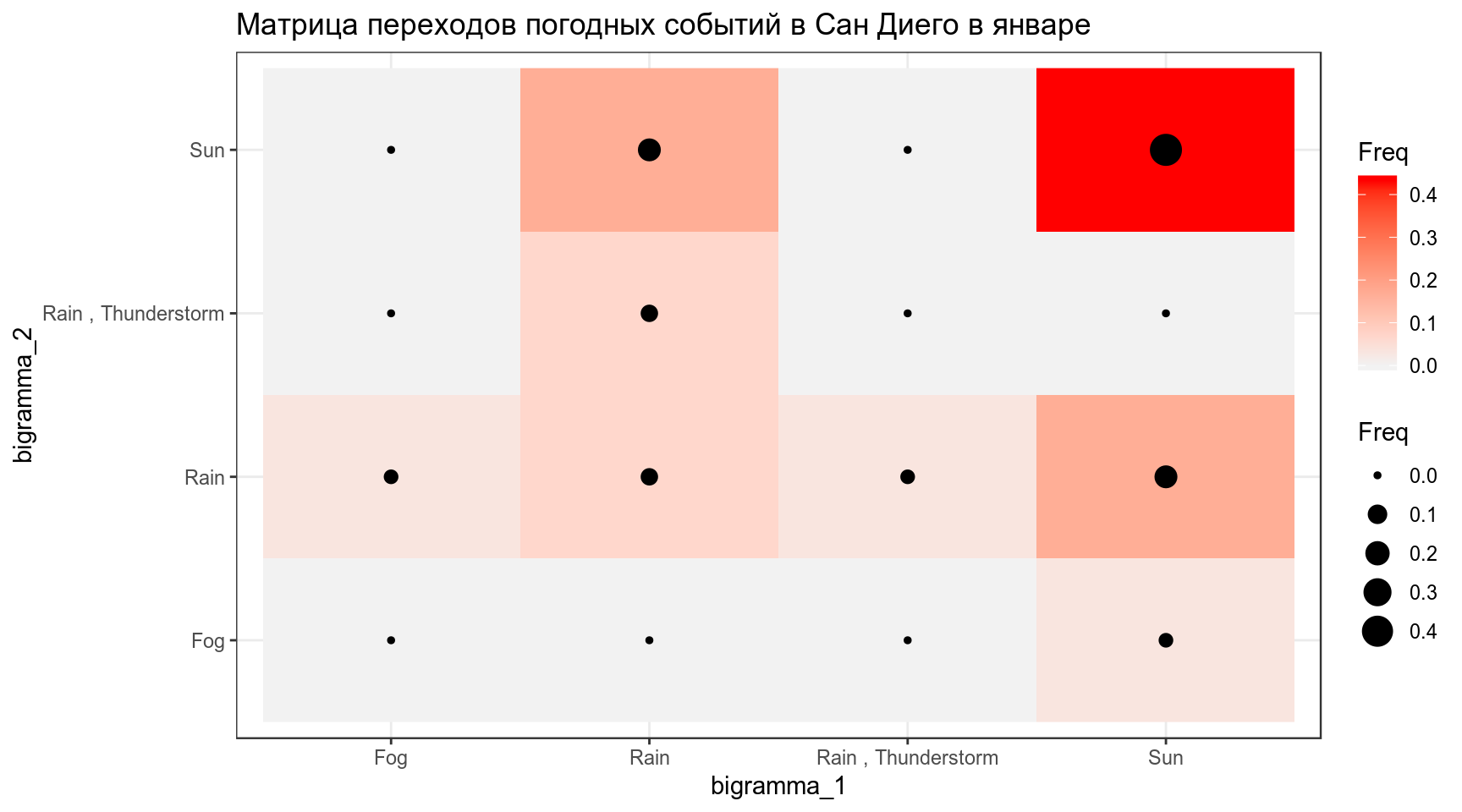
Сделаем марковскую цепь и визуализируем ее граф:
MLE Fit
A 4 - dimensional discrete Markov Chain defined by the following states:
Fog, Rain, Rain , Thunderstorm, Sun
The transition matrix (by rows) is defined as follows:
Fog Rain Rain , Thunderstorm Sun
Fog 0.00000000 1.0000000 0.0000000 0.0000000
Rain 0.00000000 0.2222222 0.2222222 0.5555556
Rain , Thunderstorm 0.00000000 1.0000000 0.0000000 0.0000000
Sun 0.05263158 0.2631579 0.0000000 0.6842105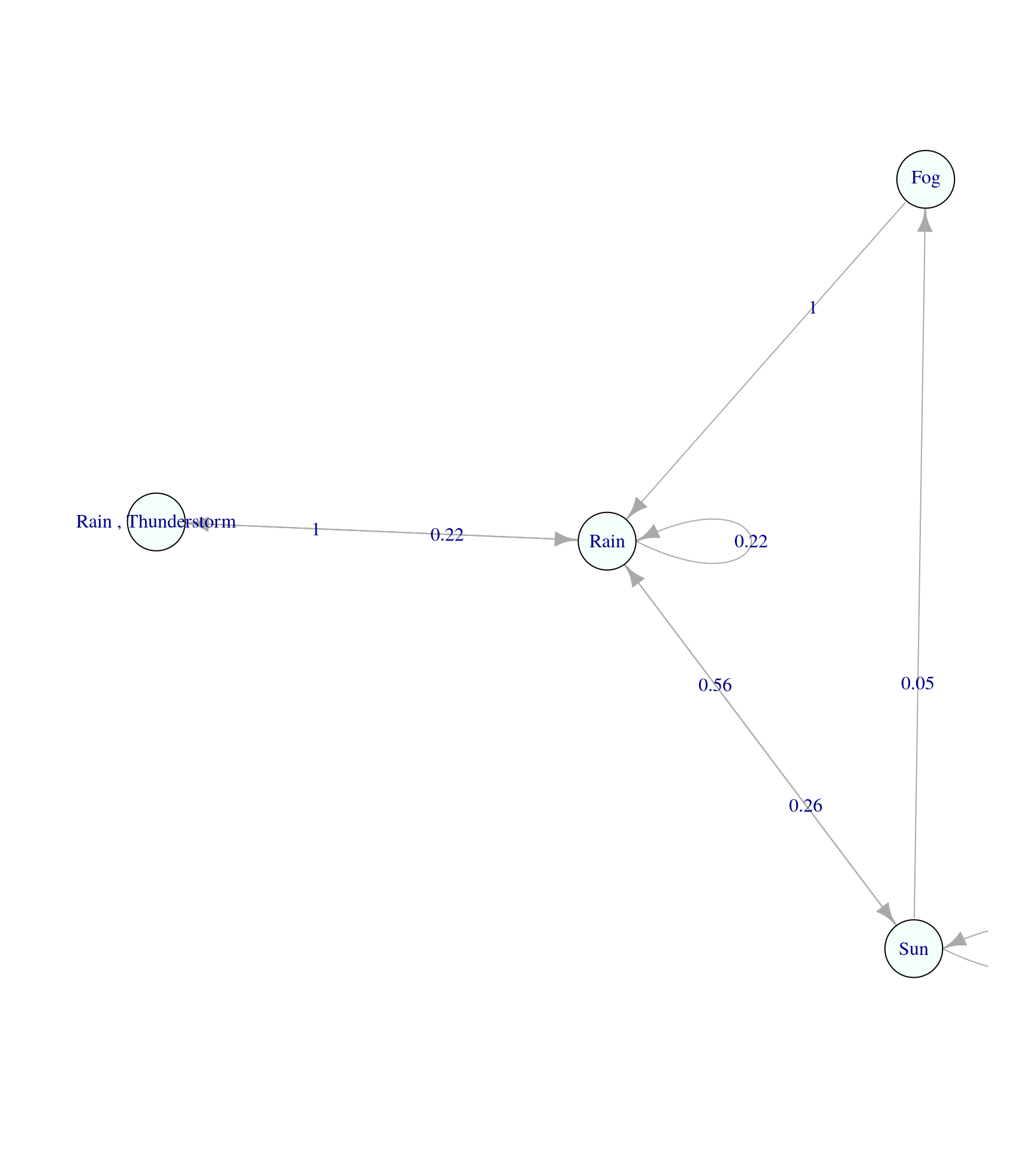
Теперь мы можем предсказать наше следующее состояние \(t_2\) перемножив матрицу начального состояния \(t_1\) (\(1 \times 4\)) на матрицу переходов (\(4 \times 4\)).
\[t_2 = t_1 \times \text{transitional matrix}\]
Предположим, что наше начальное состояние — это дождь Rain:
t_1 <- matrix(c(0, 1, 0, 0), nrow = 1)
t_1 * our_mc$estimate # это особая звездочка из пакета markovchain Fog Rain Rain , Thunderstorm Sun
[1,] 0 0.2222222 0.2222222 0.5555556Понятное дело состояние \(t_3\) это обычное произведение состояния \(t_2\) и матрицы переходов:
\[t_3 = t_2 \times \text{transitional matrix} = t_1 \times \text{transitional matrix} \times \text{transitional matrix} = t_1 \times \text{transitional matrix}^2\]
Используя полученную модель можно вычислите вероятность каждого из погодных событий на 7-ой день после дождя.
Fog Rain Rain , Thunderstorm Sun
[1,] 0.03005657 0.324639 0.07273401 0.5725704Вообще-то, часто так бывает, что цепь сходиться на каком-то состоянии (состояние эквилибриум из домашнего задания) и дальше не изменяется. Давайте Визуализируем 40 состояний цепи, если начальное состояние — дождь.
df <- as.data.frame(t_1)
colnames(df) <- sort(unique(weather$events))
sapply(2:40, function(x){
df[x,] <<- as.data.frame(as.matrix(df[1,]) * (our_mc$estimate^(x-1)))
}) [,1] [,2] [,3] [,4] [,5]
Fog 0 0.02923977 0.02650388 0.03035072 0.0296548
Rain 0.2222222 0.4178038 0.3039872 0.3386555 0.3214342
Rain , Thunderstorm 0.2222222 0.04938272 0.09284528 0.0675527 0.07525677
Sun 0.5555556 0.5035737 0.5766637 0.5634411 0.5736543
[,6] [,7] [,8] [,9] [,10]
Fog 0.03019233 0.03005657 0.03013529 0.03011125 0.03012316
Rain 0.327303 0.324639 0.325609 0.3251911 0.3253493
Rain , Thunderstorm 0.07142982 0.07273401 0.072142 0.07235756 0.07226468
Sun 0.5710748 0.5725704 0.5721137 0.5723401 0.5722628
[,11] [,12] [,13] [,14] [,15]
Fog 0.0301191 0.03012094 0.03012027 0.03012056 0.03012045
Rain 0.3252832 0.3253088 0.3252983 0.3253024 0.3253007
Rain , Thunderstorm 0.07229985 0.07228515 0.07229084 0.07228851 0.07228942
Sun 0.5722979 0.5722851 0.5722906 0.5722885 0.5722894
[,16] [,17] [,18] [,19] [,20]
Fog 0.03012049 0.03012048 0.03012048 0.03012048 0.03012048
Rain 0.3253014 0.3253011 0.3253012 0.3253012 0.3253012
Rain , Thunderstorm 0.07228905 0.0722892 0.07228914 0.07228916 0.07228915
Sun 0.5722891 0.5722892 0.5722891 0.5722892 0.5722892
[,21] [,22] [,23] [,24] [,25]
Fog 0.03012048 0.03012048 0.03012048 0.03012048 0.03012048
Rain 0.3253012 0.3253012 0.3253012 0.3253012 0.3253012
Rain , Thunderstorm 0.07228916 0.07228916 0.07228916 0.07228916 0.07228916
Sun 0.5722892 0.5722892 0.5722892 0.5722892 0.5722892
[,26] [,27] [,28] [,29] [,30]
Fog 0.03012048 0.03012048 0.03012048 0.03012048 0.03012048
Rain 0.3253012 0.3253012 0.3253012 0.3253012 0.3253012
Rain , Thunderstorm 0.07228916 0.07228916 0.07228916 0.07228916 0.07228916
Sun 0.5722892 0.5722892 0.5722892 0.5722892 0.5722892
[,31] [,32] [,33] [,34] [,35]
Fog 0.03012048 0.03012048 0.03012048 0.03012048 0.03012048
Rain 0.3253012 0.3253012 0.3253012 0.3253012 0.3253012
Rain , Thunderstorm 0.07228916 0.07228916 0.07228916 0.07228916 0.07228916
Sun 0.5722892 0.5722892 0.5722892 0.5722892 0.5722892
[,36] [,37] [,38] [,39]
Fog 0.03012048 0.03012048 0.03012048 0.03012048
Rain 0.3253012 0.3253012 0.3253012 0.3253012
Rain , Thunderstorm 0.07228916 0.07228916 0.07228916 0.07228916
Sun 0.5722892 0.5722892 0.5722892 0.5722892 df %>%
mutate(stage = 1:40) %>%
gather(events, value, Fog:Sun) %>%
ggplot(aes(stage, value, color = events))+
geom_line(show.legend = FALSE)+
directlabels::geom_dl(aes(label = events), method = "last.qp")+
labs(title = 'Марковская цепь погодных событий в Сан Диего в январе',
caption = "начальное состояние --- дождь (Rain)")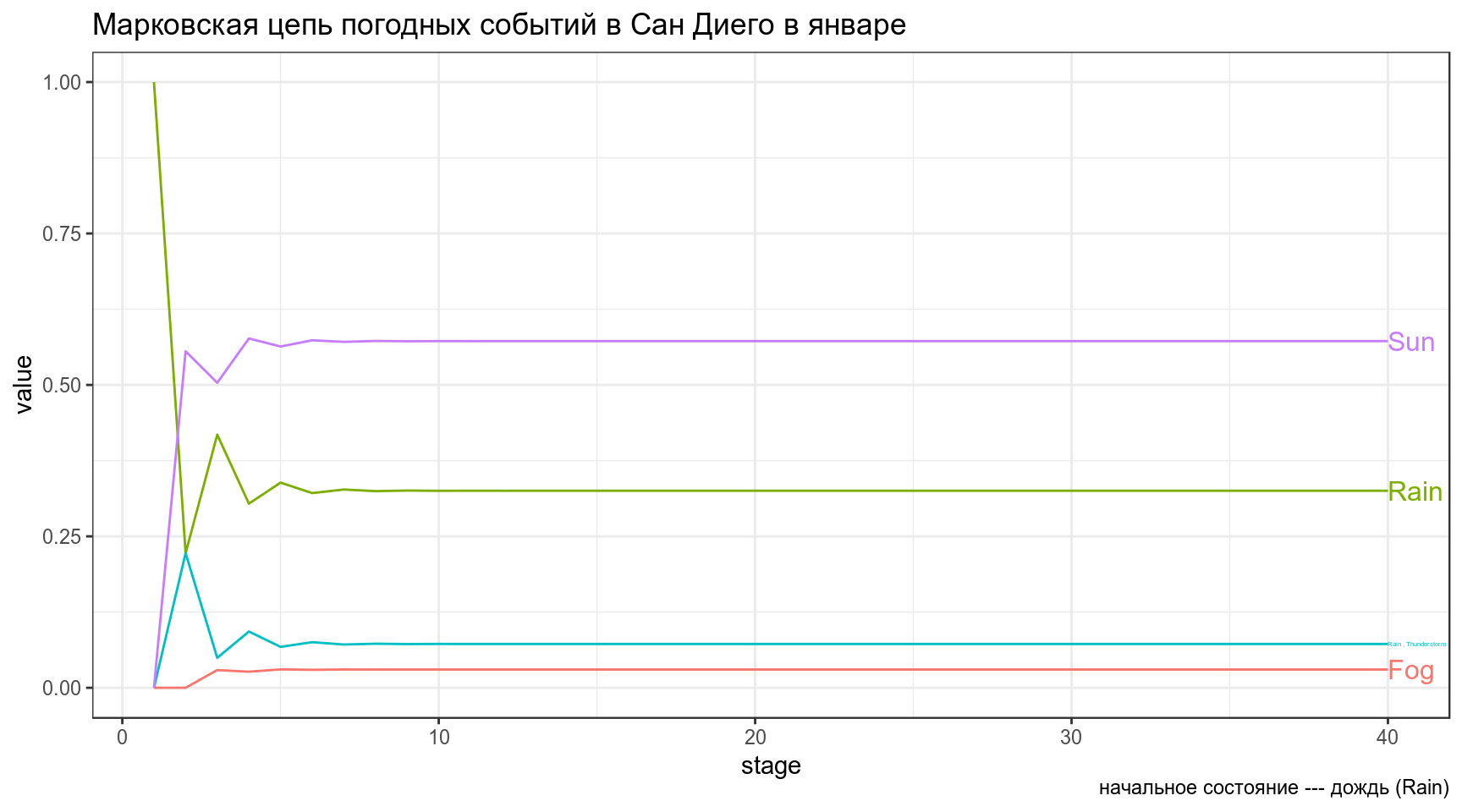
И люди вообще-то научились вычислять такие вещи на основании цепи:
Fog Rain Rain , Thunderstorm Sun
[1,] 0.03012048 0.3253012 0.07228916 0.57228923 Что дальше?
- легко придумать обобщение этой логики на непрерывные данные
- можно придумать вариант, когда мы пытаемся предсказать некоторые ненаблюдаемые вещи на основании наблюдаемых: например, погоду в Сан Диего на основании настроение вашего друга, которому вы каждый день звоните. Это называется скрытые марковские цепи.
Задачи
4.1
Скачайте датасет, который содержит роман “По эту сторону рая” Ф. С. Фицджеральда:
token— словоPOS— часть речи, полученная на основе английской модели UDPIPE.
Визуализируйте частоты частей речи в романе: 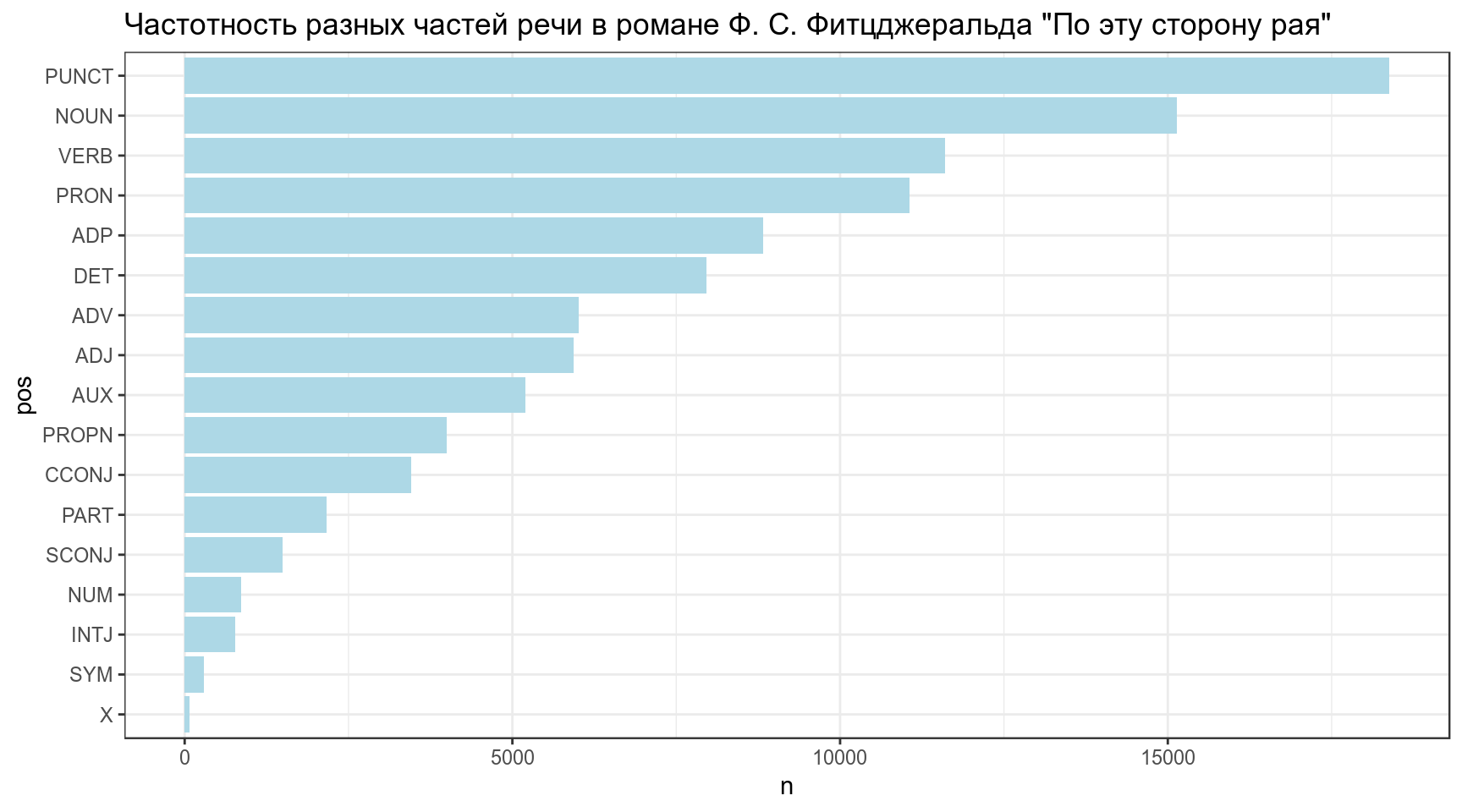
4.2
Визуализируйте матрицу последовательных переходов частей речи: 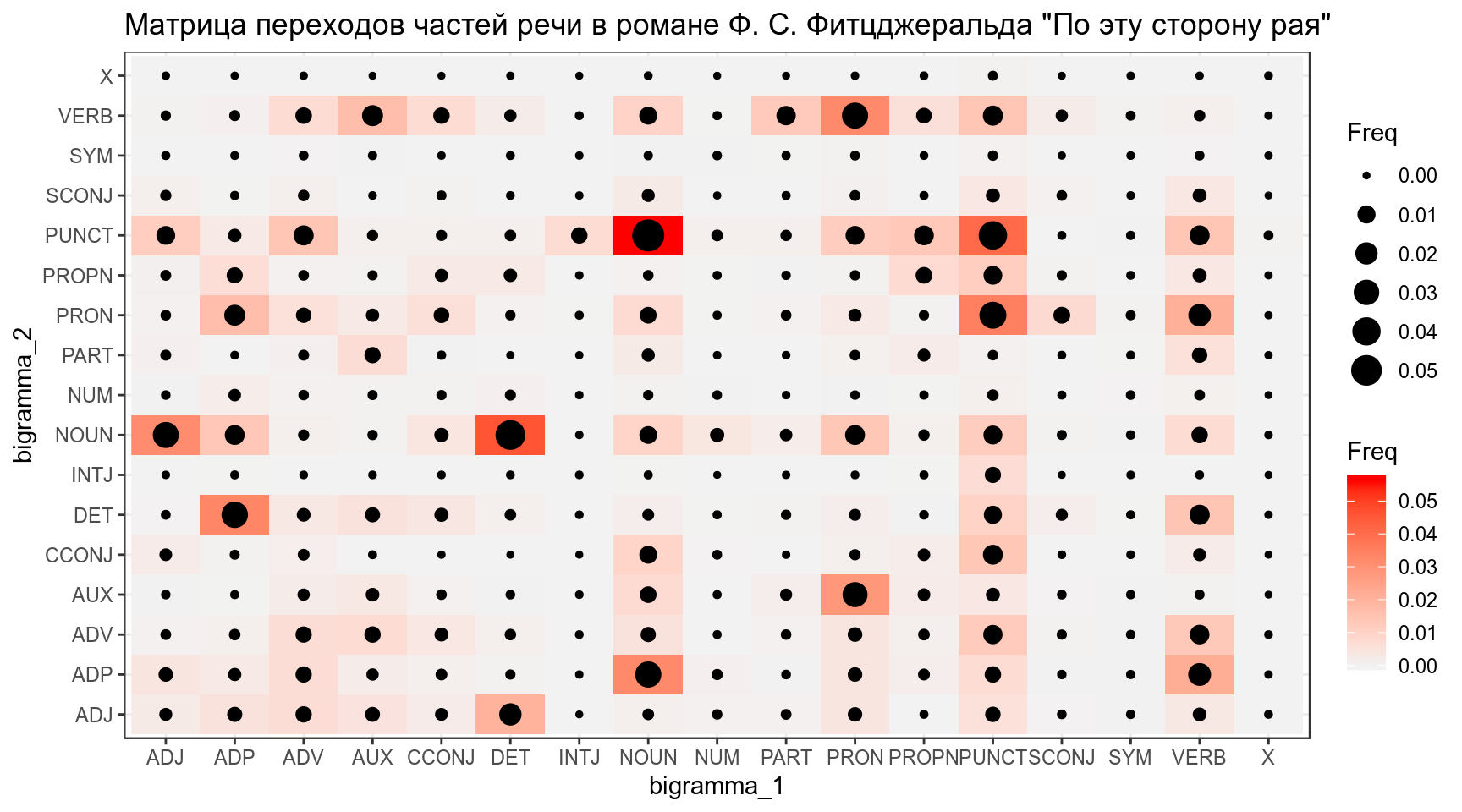
4.3
Сделайте марковскую цепь и визуализируйте ее граф: 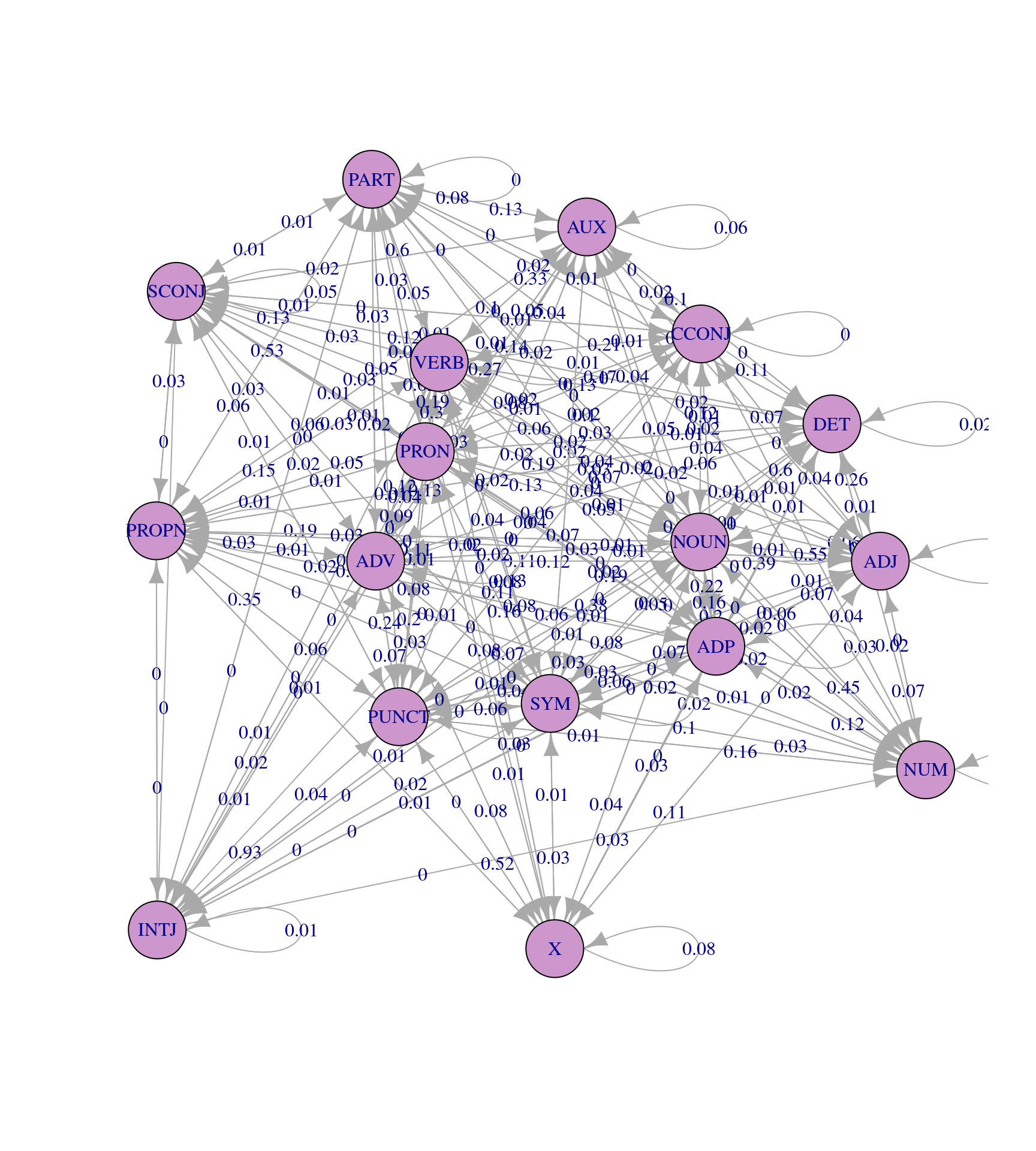
4.4
Используя полученную модель, вычислите вероятность встретить после артикля (DET) прилагательное (ADJ) (с точностью до трех знаков после запятой).
4.5
Используя полученную модель, вычислите вероятность встретить после артикля прилагательное в четвертом по счету слове (с точностью до трех знаков после запятой).
ADJ ADP ADV AUX CCONJ DET
[1,] 0.06364596 0.07437913 0.05648417 0.05594779 0.03150212 0.0760366
INTJ NOUN NUM PART PRON PROPN
[1,] 0.008021889 0.1565543 0.008617353 0.01814057 0.1067079 0.04168071
PUNCT SCONJ SYM VERB X
[1,] 0.1700765 0.01359084 0.00284206 0.1150473 0.00072474234.6
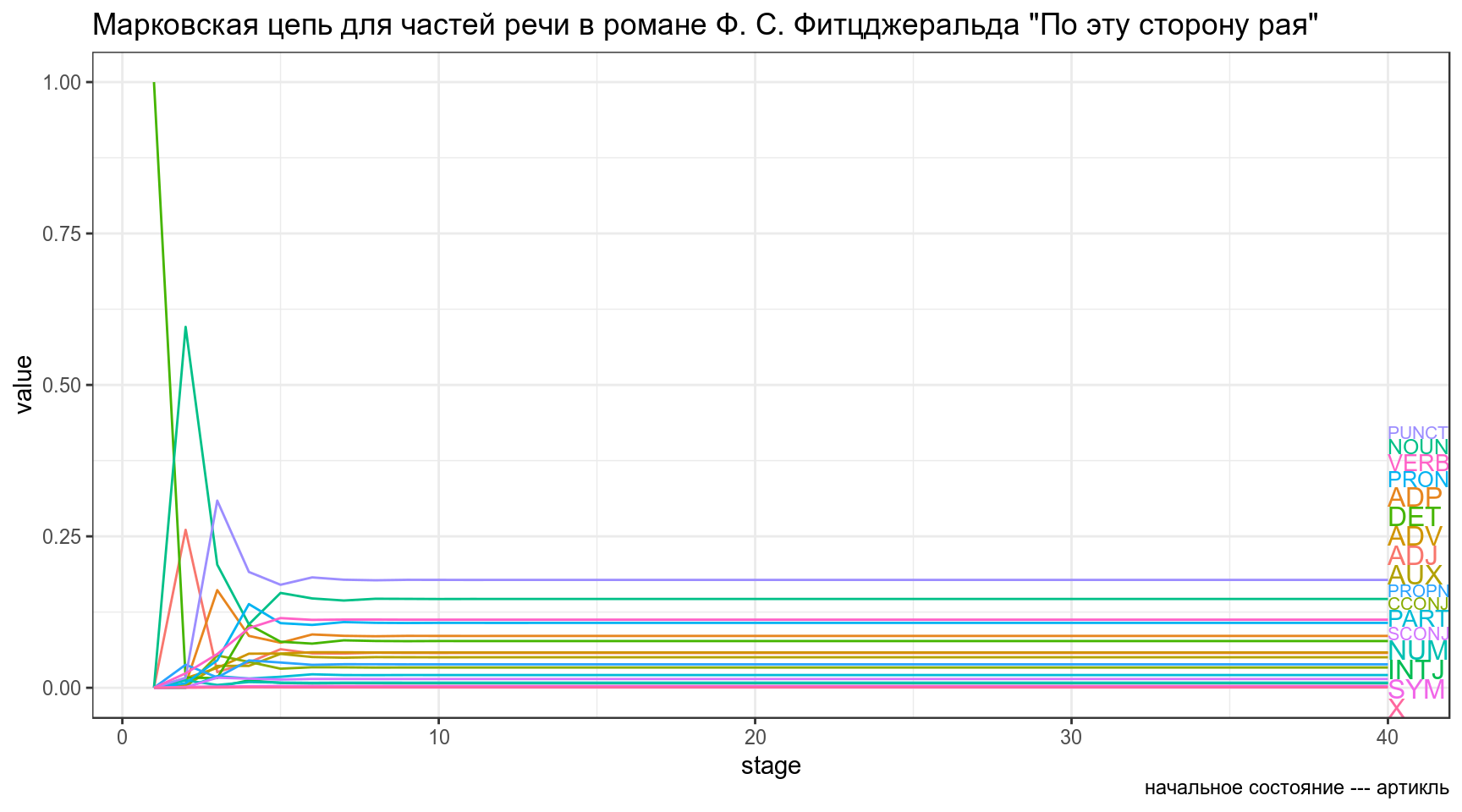
Визуализируйте 40 состояний цепи, если начальное состояние — артикль (DET).
4.7
Посчитайте фиксированные состояния цепи. В ответе приведите значение для местоимения (с точностью до трех знаков после запятой).
