5. Байес фактор
Г. Мороз
1. Формула Байеса опять
\[P(θ|Data) = \frac{P(Data|θ)\times P(θ)}{P(Data)}\]
\[\frac{P(θ|Data)}{P(θ)} = \frac{P(Data|θ)}{P(Data)}\]
Левая часть этого уравнения описывает вероятности относительно параметров, и эти вероятности представляют собой наши представления. Доля описывает, как наши представления относительно параметра θ обновляются в свете данных.
Байесовский фактор берется из этой же формулы:
\[\frac{\frac{P(M_A|Data)}{P(M_A)}}{\frac{P(M_B|Data)}{P(M_B)}} = \frac{\frac{P(Data|M_A)}{P(Data)}}{\frac{P(Data|M_B)}{P(Data)}} = \frac{P(Data|M_A)}{P(Data|M_B)} = BF_{AB}\]
Т. е. байесовский фактор по сути это всего лишь пропорция составленная из двух функций правдоподобия.
В датасете c грибами (взят c kaggle) представлено следующее распределение по месту обитания:
df <- read_csv("https://github.com/agricolamz/2019_BayesDan_winter/blob/master/datasets/mushrooms.csv?raw=true")
df %>%
count(class, habitat) %>%
group_by(class) %>%
mutate(prop = n/sum(n)) %>%
ggplot(aes(class, prop, fill = habitat, label = round(prop, 3)))+
geom_col()+
geom_text(position = position_stack(vjust = 0.5), color = "white")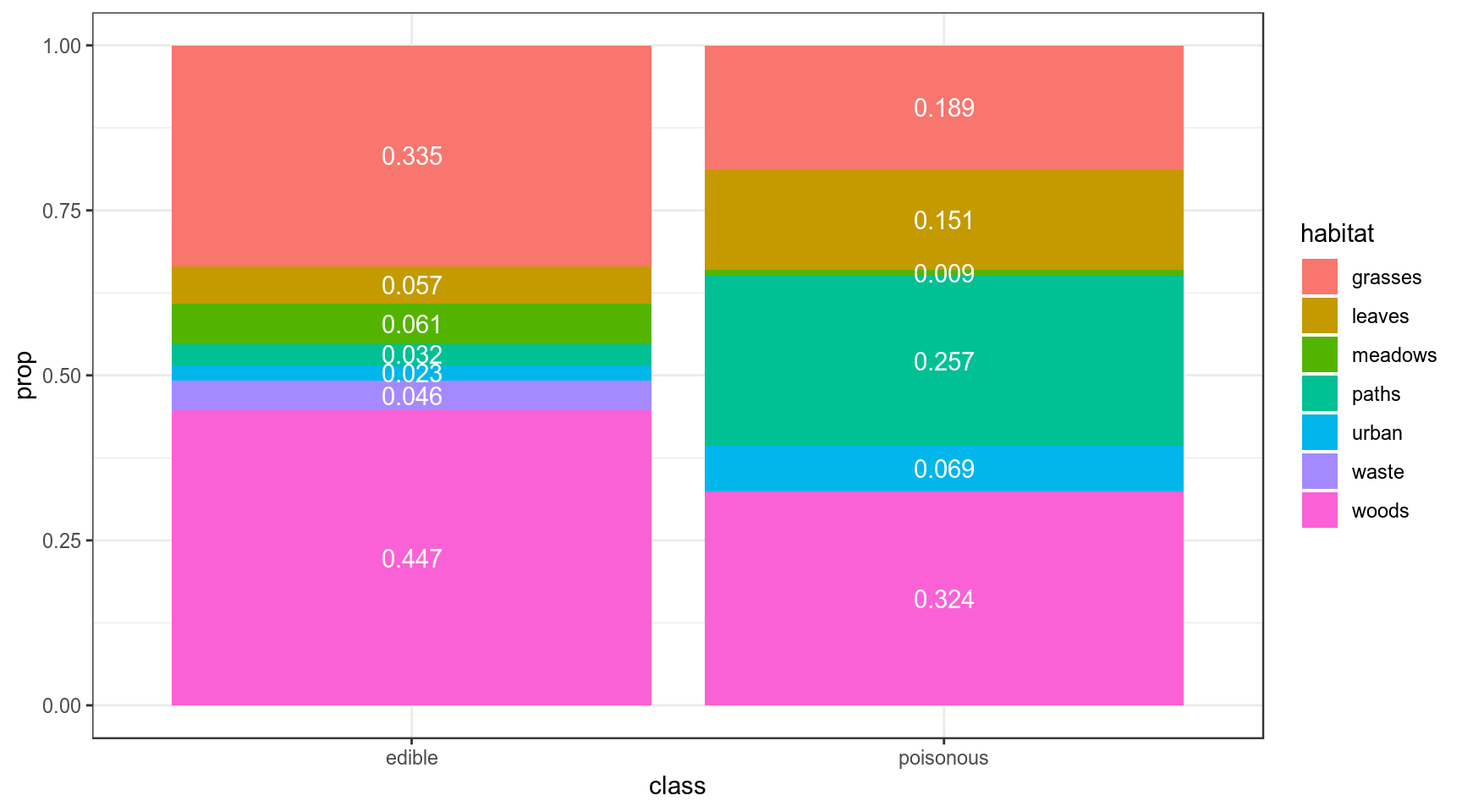
Мы нашли некоторый новый вид грибов на лужайке (grasses), а потом в лесу (woods). Давайте посчитаем \(BF_{edible\ poisonous}\):
\[L(grasses,\ wood|edible) = 0.335 \times 0.447 = 0.149745\]
\[L(grasses,\ wood|poisonous) = 0.189 \times 0.324 = 0.061236\]
\[BF_{edible\ poisonous} = \frac{L(grasses,\ wood|edible)}{L(grasses,\ wood|poisonous)} = \frac{0.149745}{0.061236} = 2.445375\]
1.2
Вашего друга похитили а на почту отправили датасет, в котором записаны данные о погоде из пяти городов. Ваш телефон зазвонил, и друг сказал, что не знает куда его похитили, но за окном легкий дождь (Rain). А на следующий день — сильный дождь (Rain Thunderstorm). Посчитайте \(BH_{San\_Diego\ Auckland}\) с точностью до 1 знака после запятой.
