1. Распределения
Г. Мороз
1. Распределения в R
В R встроено какое-то количество известных распределений. Все они представлены четырьмя функциями:
d...(функция плотности, probability density function),p...(функция распределения, cumulative distribution function) — интеграл площади под кривой от начала до указанной квантилиq...(обратная функции распределения, inverse cumulative distribution function) — значение p-той квантили распределения- и
r...(рандомные числа из заданного распределения).
Рассмотрим все это на примере нормального распределения.
data_frame(x = 1:100,
PDF = dnorm(x = x, mean = 50, sd = 10)) %>%
ggplot(aes(x, PDF))+
geom_point()+
labs(title = "PDF нормального распределения (μ = 50, sd = 10)")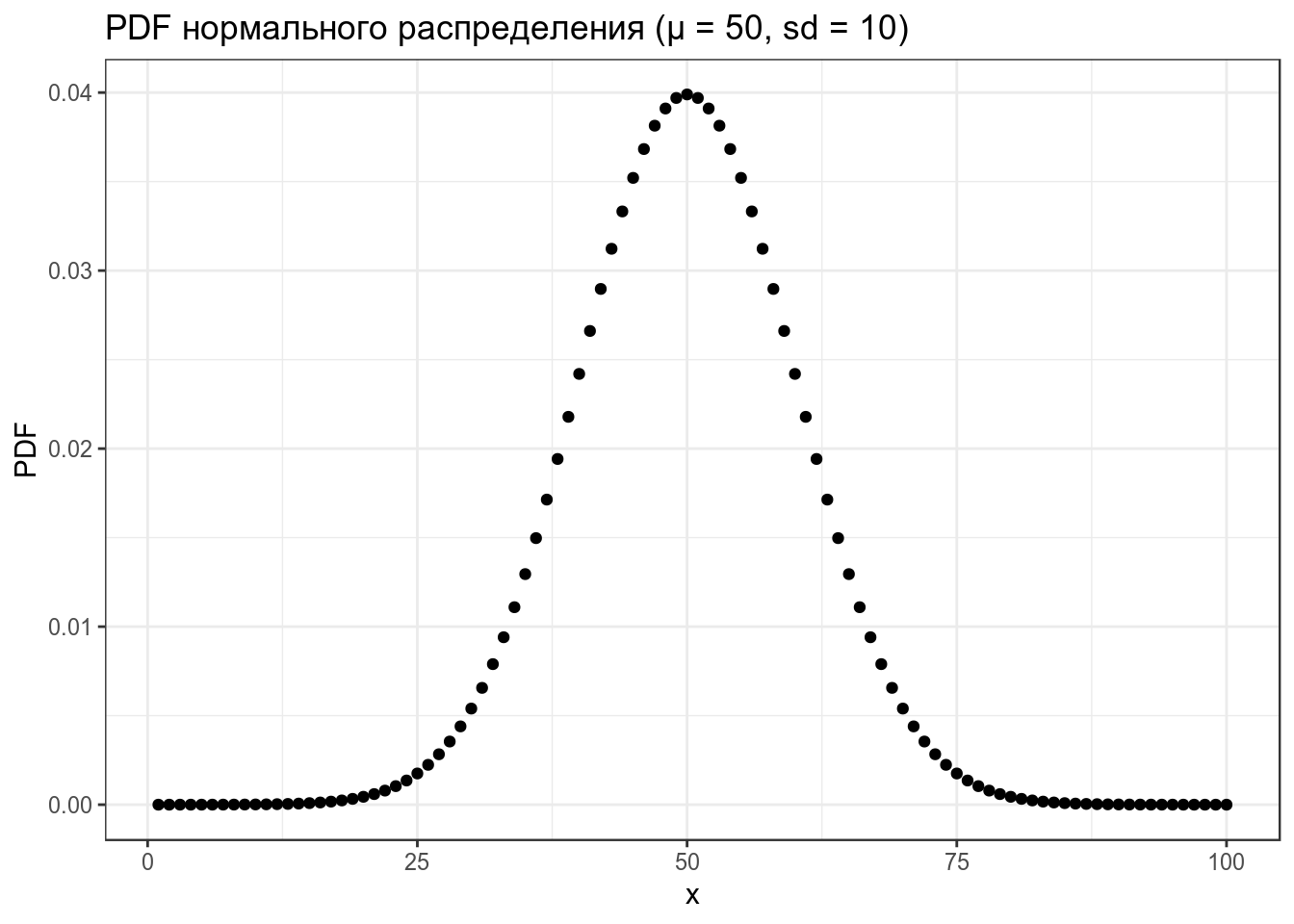
data_frame(x = 1:100,
CDF = pnorm(x, mean = 50, sd = 10)) %>%
ggplot(aes(x, CDF))+
geom_point()+
labs(title = "CDF нормального распределения (μ = 50, sd = 10)")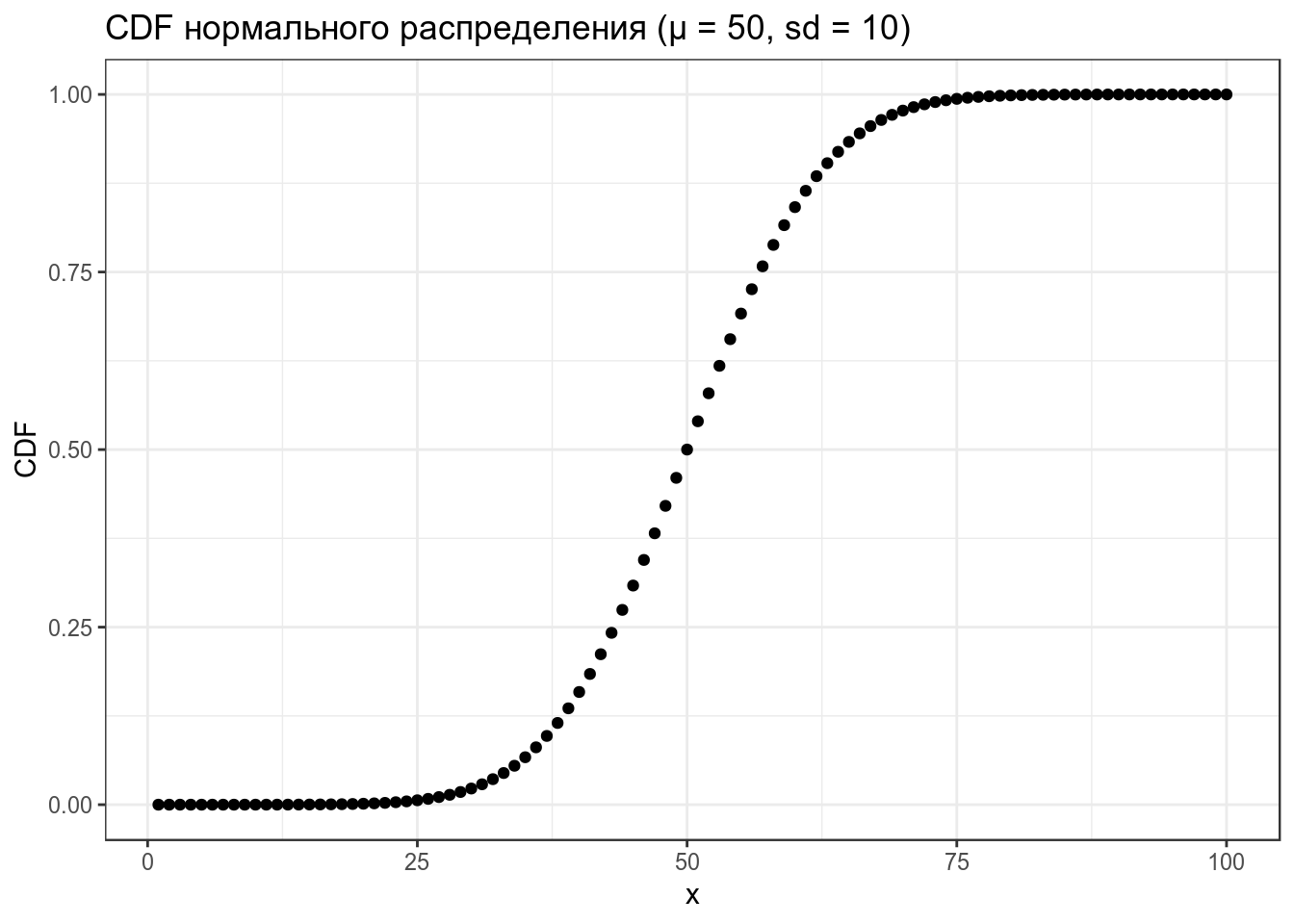
data_frame(quantiles = seq(0, 1, by = 0.01),
value = qnorm(quantiles, mean = 50, sd = 10)) %>%
ggplot(aes(quantiles, value))+
geom_point()+
labs(title = "inverse CDF нормального распределения (μ = 50, sd = 10)")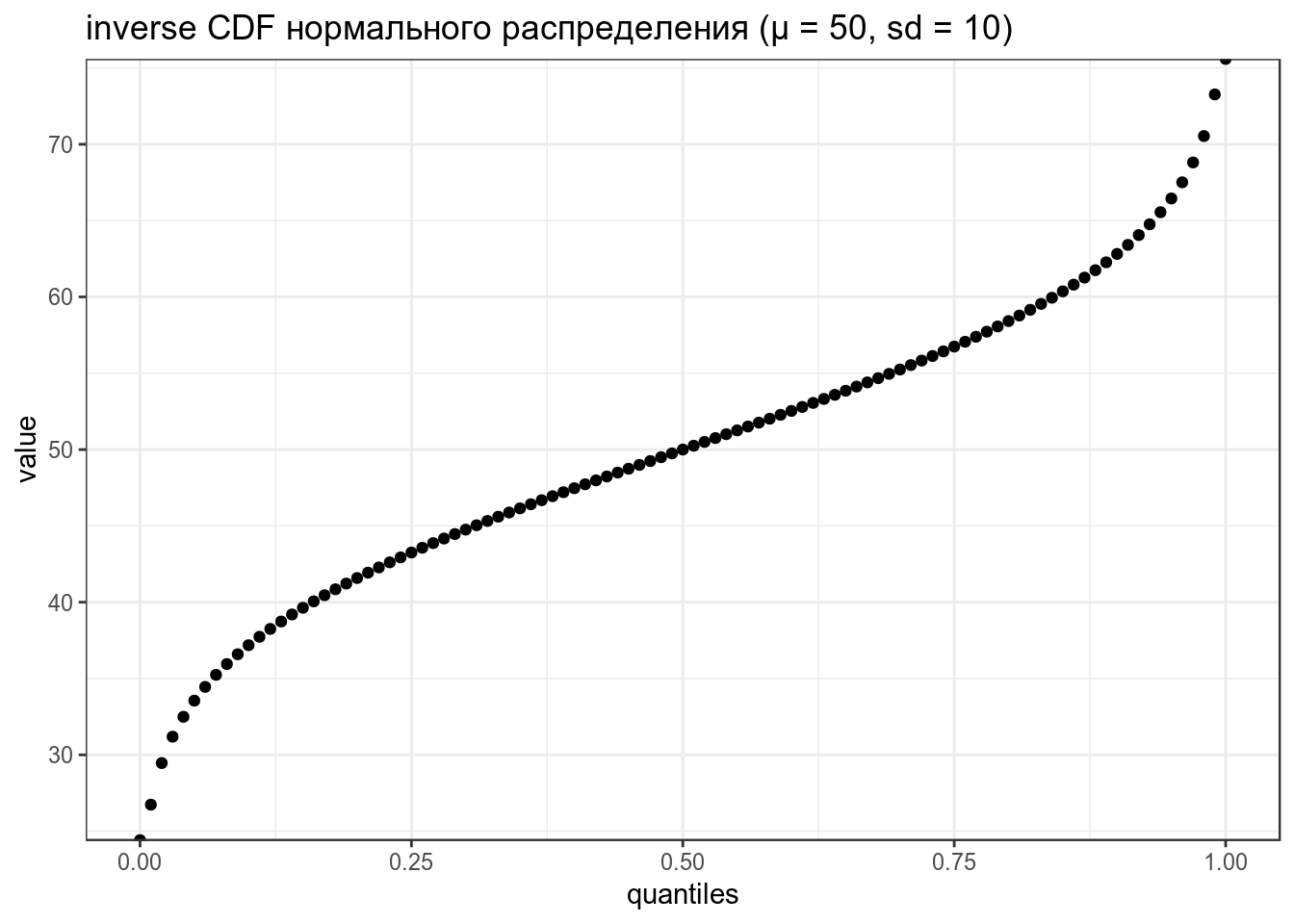
data_frame(sample = rnorm(100, mean = 50, sd = 10)) %>%
ggplot(aes(sample))+
geom_histogram()+
labs(title = "выборка нормально распределенных чисел (μ = 50, sd = 10)")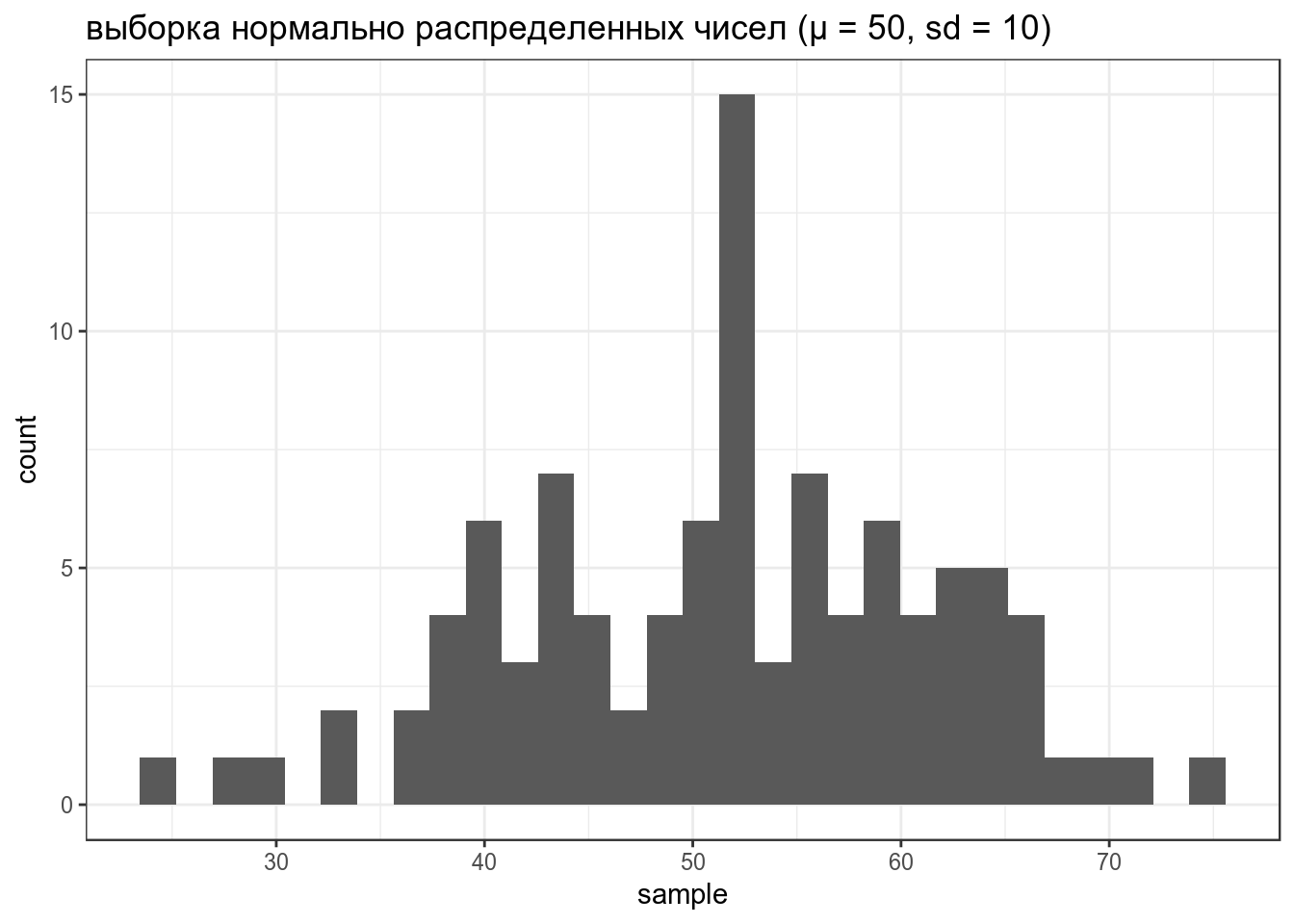
Если не использовать set.seed(), то результат работы рандомизатора нельзя будет повторить.
1.1
Какое значение имеет 25% квантиль нормального распределения со средним в 20 и стандартным отклонением 90.
1.2
Посчитайте z-score для 97% квантили нормально распределенных данных.
2. Дискретные распределения
2.1 Биномиальное распределение
Биномиальное распределение — распределение количетсва успехов эксперементов Бернулли из n попыток с вероятностью успеха p.
\[P(k | n, p) = \frac{n!}{k!(n-k)!} \times p^k \times (1-p)^{n-k} = {n \choose k} \times p^k \times (1-p)^{n-k}\] \[ 0 \leq p \leq 1; n, k > 0\]
data_frame(x = 0:50,
density = dbinom(x = x, size = 50, prob = 0.16)) %>%
ggplot(aes(x, density))+
geom_point()+
geom_line()+
labs(title = "Биномиальное распределение p = 0.16, n = 50")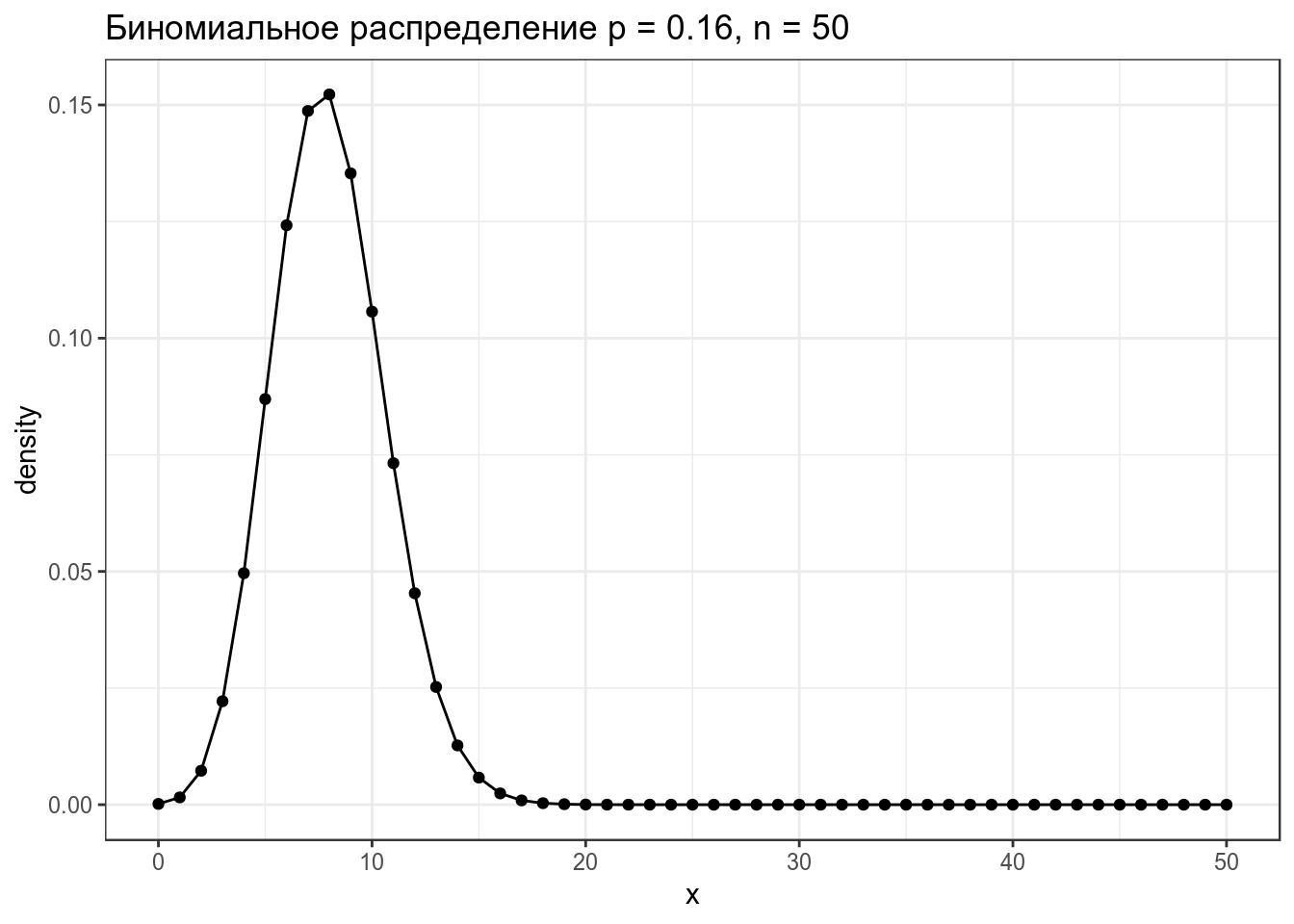
2.2 Геометрическое распределение
Геометрическое распределение — распределение количетсва эксперементов Бернулли с вероятностью успеха p до первого успеха.
\[P(k | p) = (1-p)^k\times p\] \[k\in\{1, 2, \dots\}\]
data_frame(x = 0:50,
density = dgeom(x = x, prob = 0.16)) %>%
ggplot(aes(x, density))+
geom_point()+
geom_line()+
labs(title = "Геометрическое распределение p = 0.16, n = 50")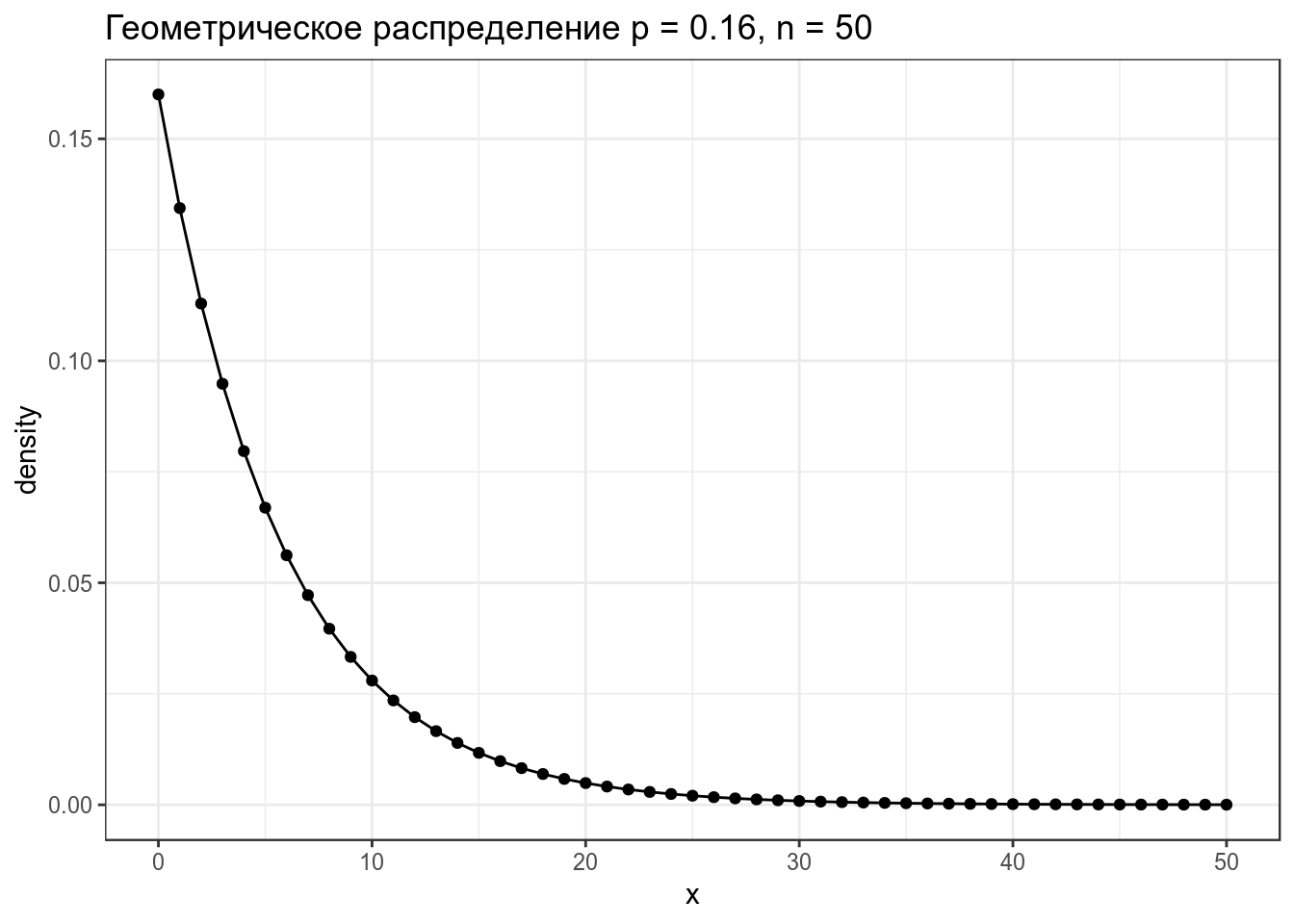
2.3 Мультиномиальное распределение
Мультиномиальное распределение — обобщение биноимального эксперимента на случай n независимых испытаний с k исходами с вероятностями каждого исхода \(p_1, p_2, \dots p_k\).
\[P(x_1, \dots, x_k | n, p_1, \dots p_k) = \frac{n!}{x_1!\times\dots\times x_k!} \times p_1^{x_1}\times\dots\times p_2^{x_k}\] \[ x_i \in \{0, n\}, i \in \{1, k\}, \sum_{i=1}^kx_i = n \]
Если у нас есть три взаимисключающих исхода V1, V2 и V3 с верятностями \(p_1 = 0.4, p_2 = 0.35\) и \(p_3 = 0.25\), какова вероятность получить V1 7 раз, V2 3 раза и V3 2 раза?
[1] 0.03477197А как выглядит распределение?
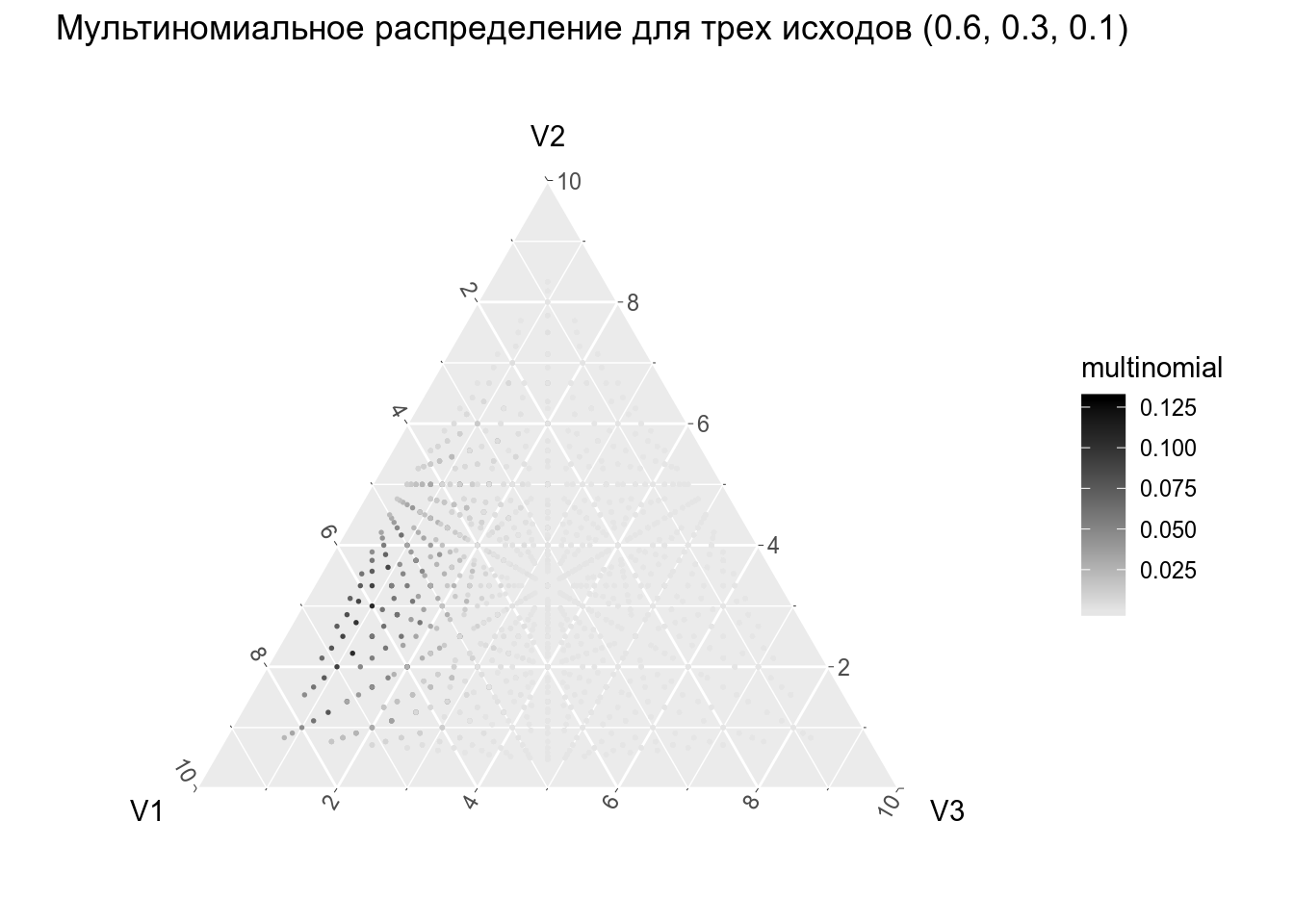
3. Непрерывные распределения
3.1 Нормальное распределение
\[P(x) = \frac{1}{\sigma\sqrt{2\pi}}\times e^{-\frac{\left(x-\mu\right)^2}{2\sigma^2}}\]
\[\mu \in \mathbb{R}; \sigma^2 > 0\]
data_frame(x = 1:100,
PDF = dnorm(x = x, mean = 50, sd = 10)) %>%
ggplot(aes(x, PDF))+
geom_point()+
geom_line()+
labs(title = "PDF нормального распределения (μ = 50, sd = 10)")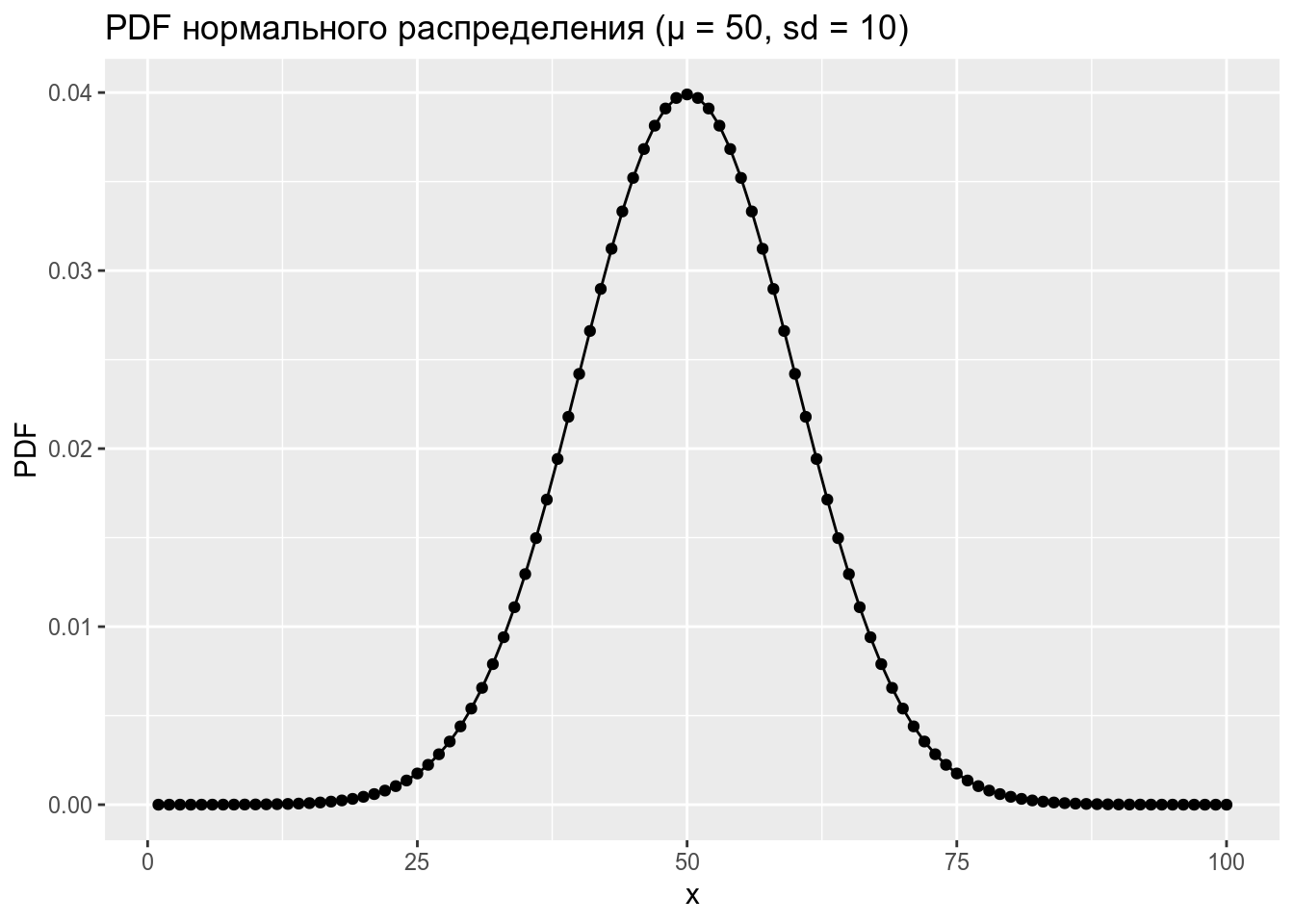
3.2 Логнормальное распределение
\[P(x) = \frac{1}{\sqrt{x\sigma2\pi}}\times e^{-\frac{\left(\ln(x)-\mu\right)^2}{2\sigma^2}}\]
\[\mu \in \mathbb{R}; \sigma^2 > 0\]
data_frame(x = 1:100,
PDF = dlnorm(x = x, mean = 3, sd = 0.5)) %>%
ggplot(aes(x, PDF))+
geom_point()+
geom_line()+
labs(title = "PDF логнормального распределения (μ = 4, sd = 0.5)")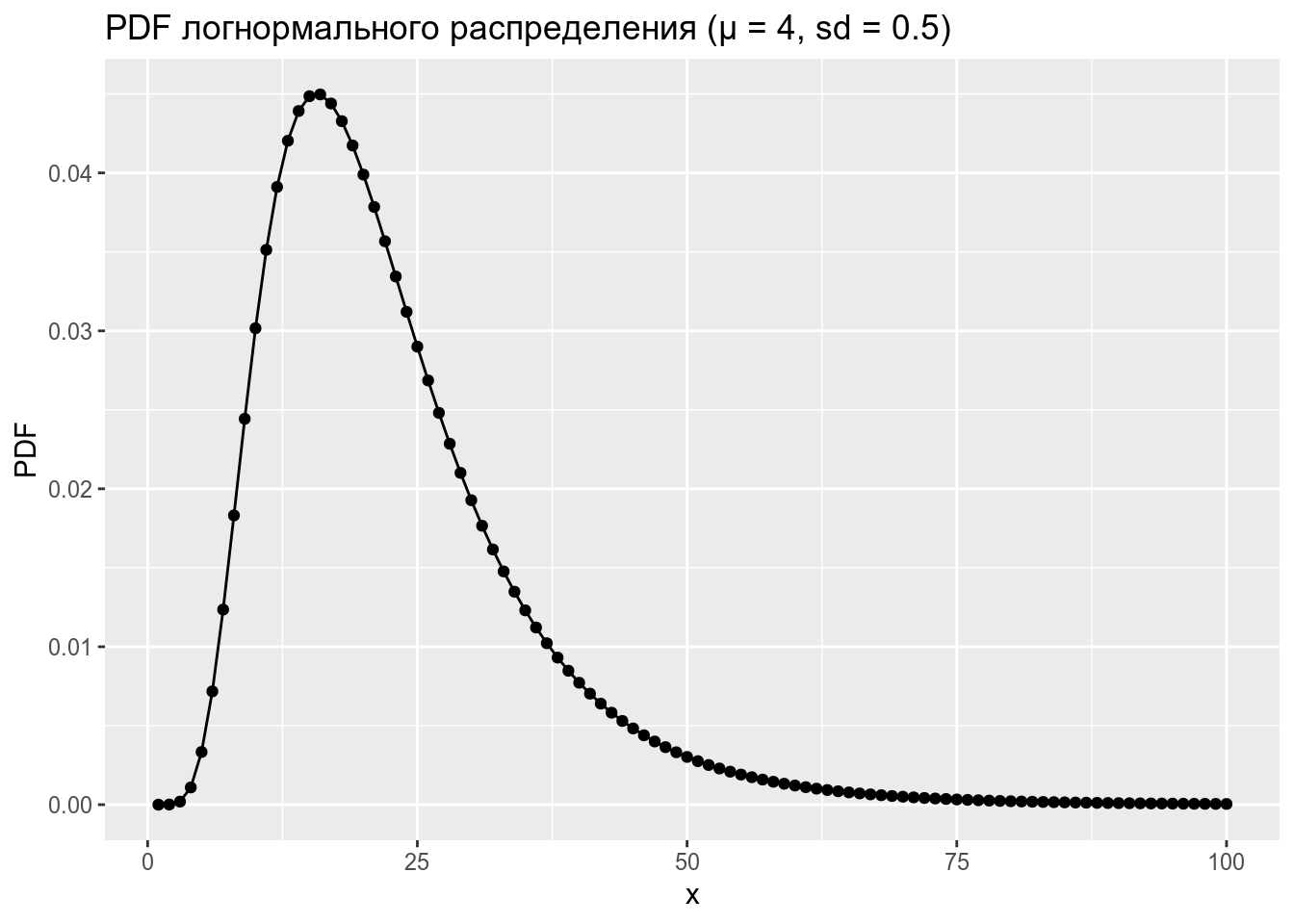
3.3 Экспоненциальное распределение
\[P(x)= \lambda \times e^{-\lambda x}\]
data_frame(x = 1:20,
PDF = dexp(x = x, rate = 5)) %>%
ggplot(aes(x, PDF))+
geom_point()+
geom_line()+
labs(title = "PDF экспоненциального распредления")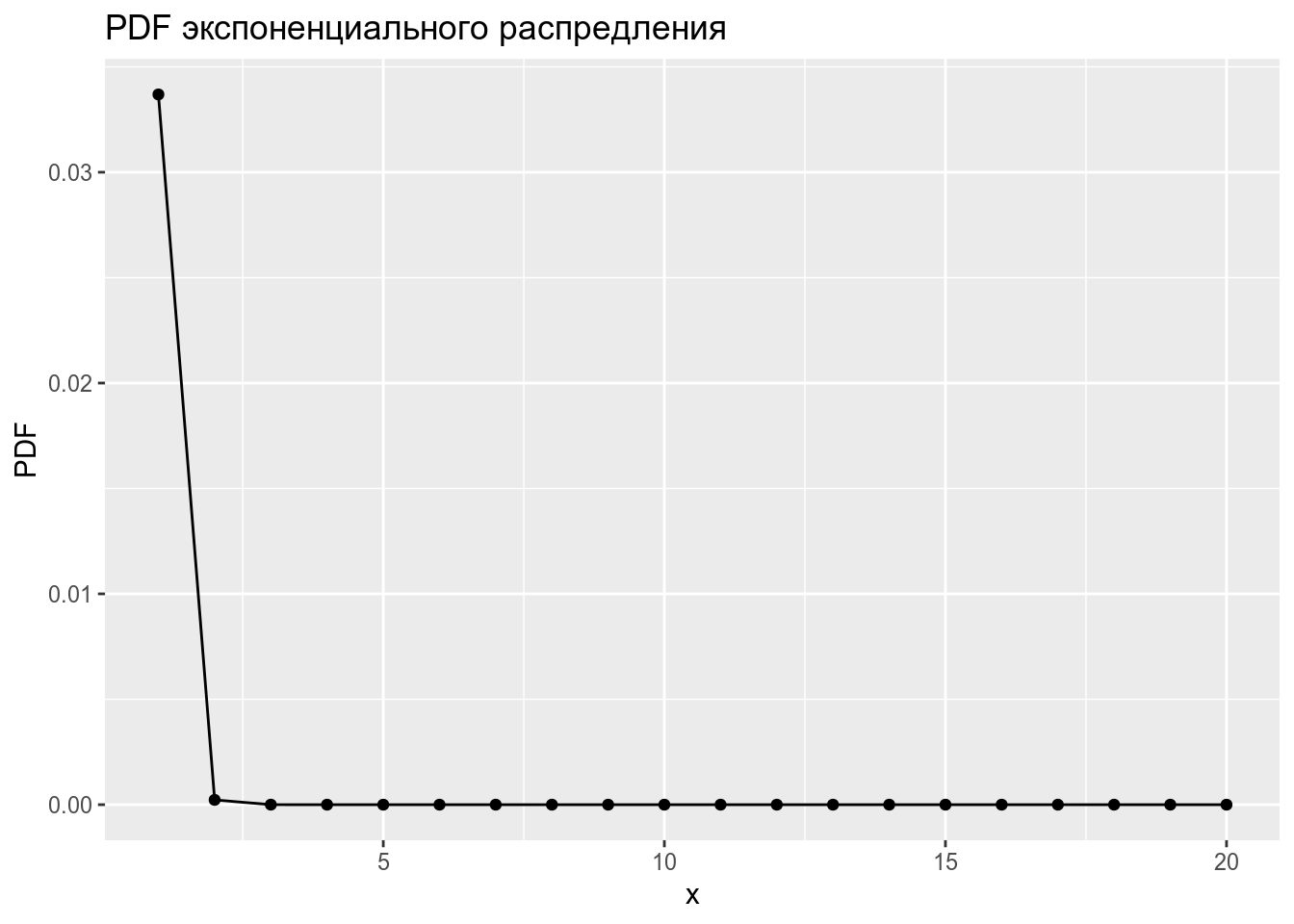
4. Вероятность vs. функция правдободобия
Предположим что распределение количества согласных в языках мира можно описать нормальным распределением со средним 22, и стандартным отклонением 6:
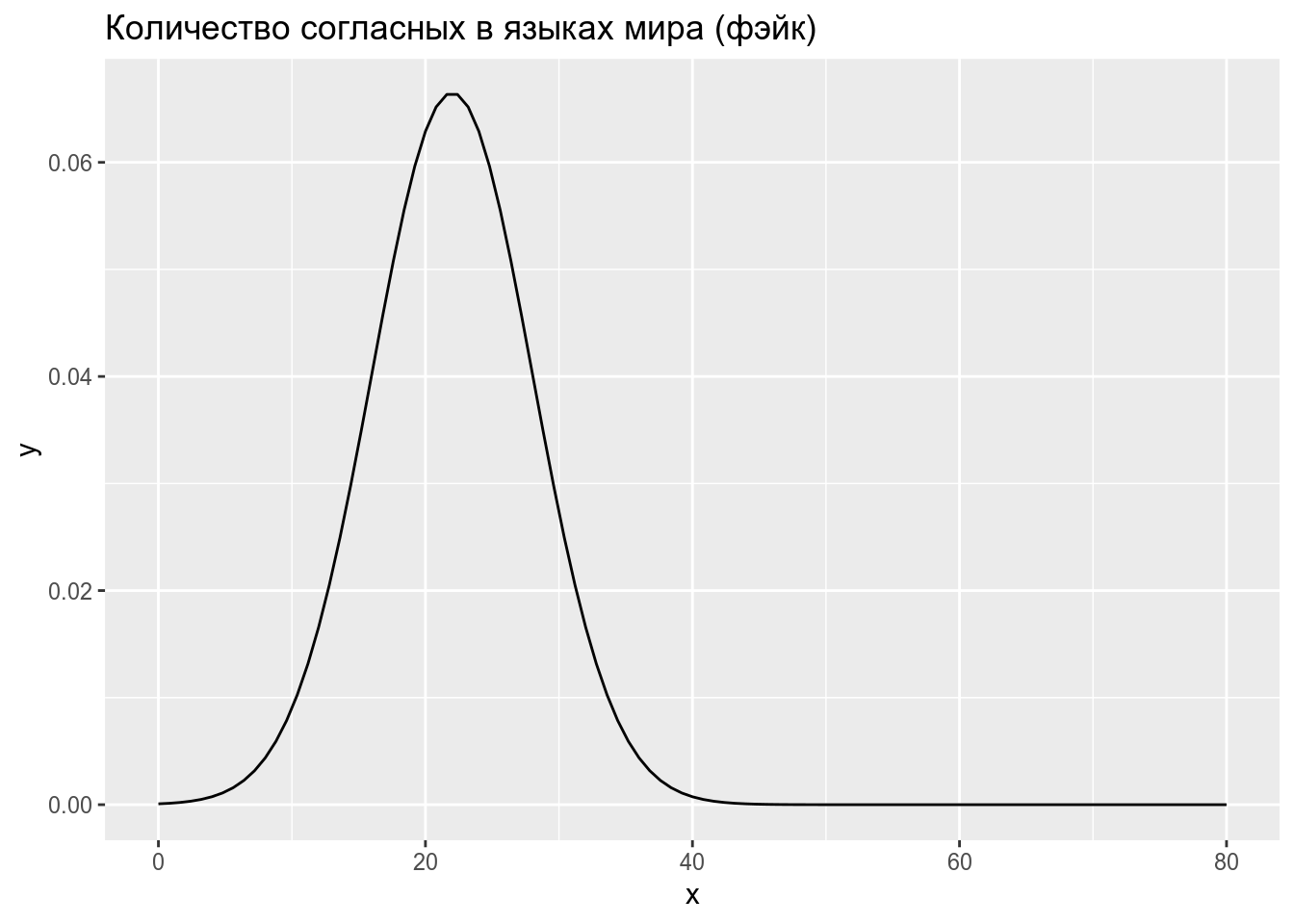
Тогда вероятность того, что в выбранных произвольно языках окажется от 23 до 32 согласных равна интегралу нормального распределения в указанном промежутке:
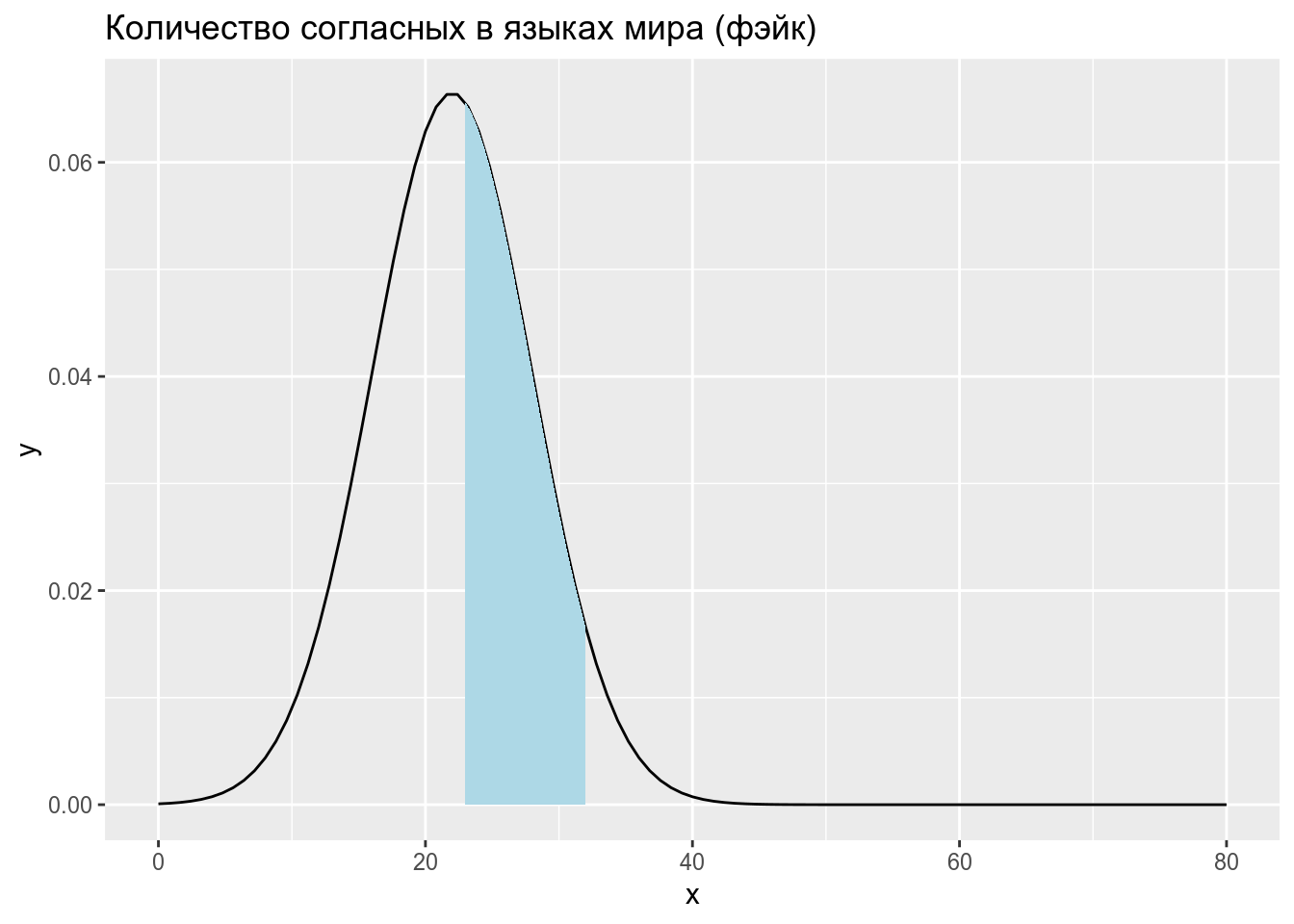
\[P\left(X \in (23,\, 32) | X \sim \mathcal{N}(\mu = 22,\, \sigma^{2}=6)\right) = ...\]
[1] 0.3860258Когда мы говорим про функцию правдоподобия, то мы уже нашли еще один язык в котором оказалось 33 согласных. Нас интересует, насколько правдоподобна функция нормального распределения со средним 22 и стандартным отклонением 6 при значении переменной 33. Это значение равно функции плотности:
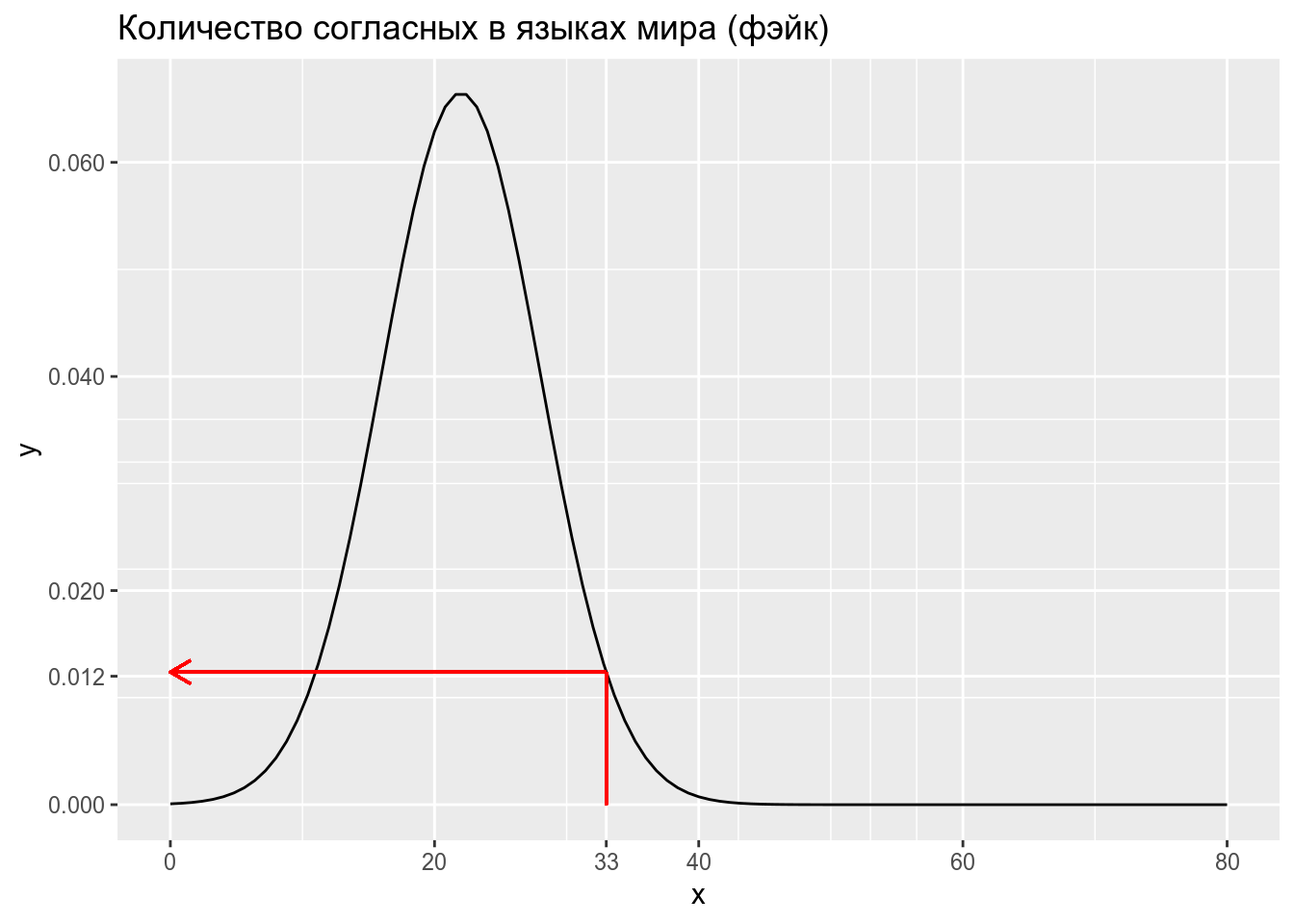
\[L\left(X \sim \mathcal{N}(\mu = 22,\, \sigma^{2}=6)|x = 33\right) = ...\]
[1] 0.01238519В итоге:
- вероятность — P(data|distribution)
- правдоподобие — L(distribution|data)
Домашнее задание 1 (до 12.12.2018)
Вспомните пожалуйста, условные вероятности, формулу Байеса и при каких условиях ее применяют.
- Визуализация условной вероятности
Домашнее задание 1 (до 19.12.2018)
Домашнее задание нужно выполнять в отдельном rmarkdown файле. Получившийся файл следует помещать в соответствующую папку в своем репозитории на гитхабе. Более подробные инструкции см. на этой странице.
1.1
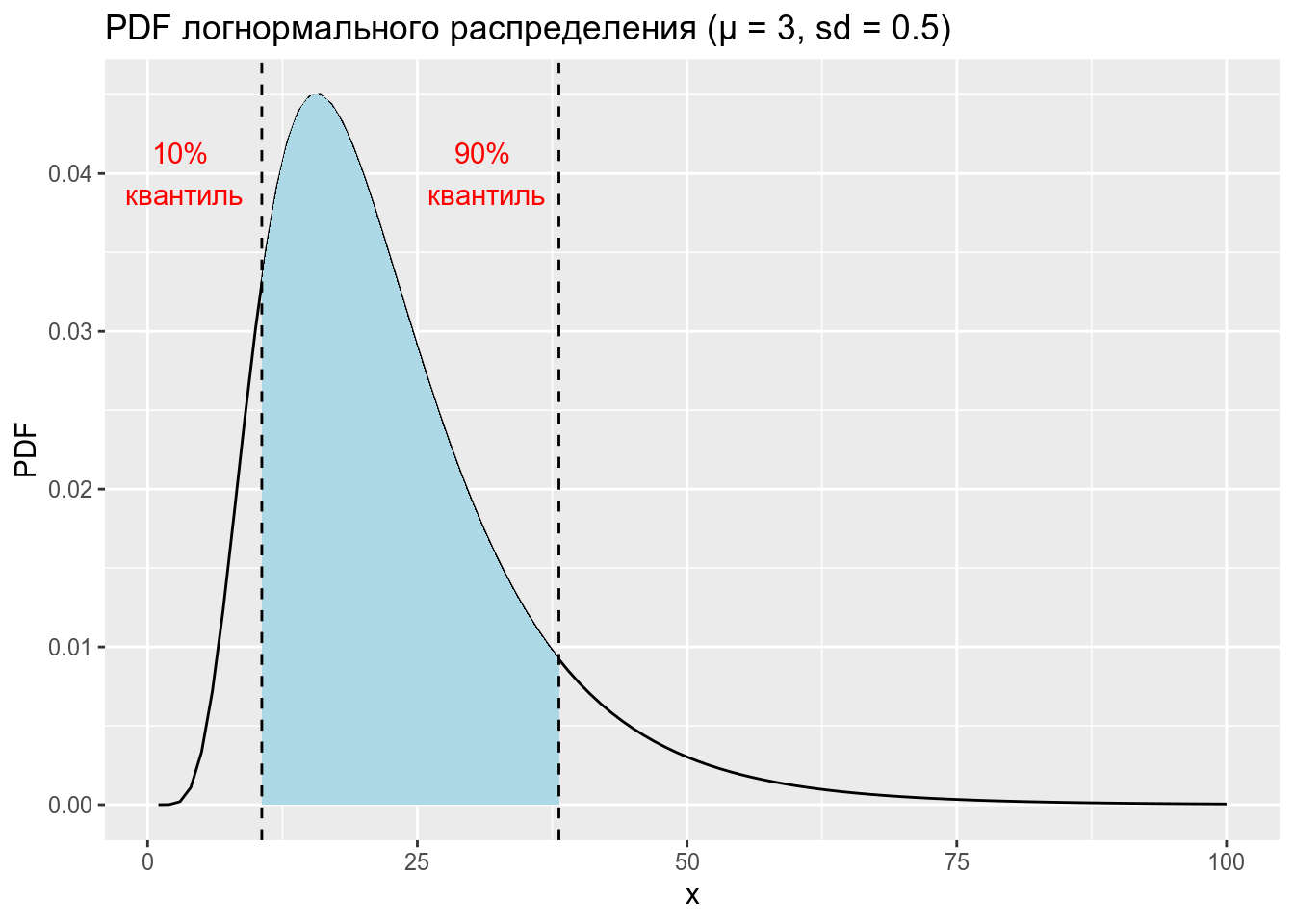
Дан график логнормального распределения со средним 3 и стандартным отклонением 0.5. Используйте функцию integrate, чтобы посчитать закрашенную площадь под кривой.
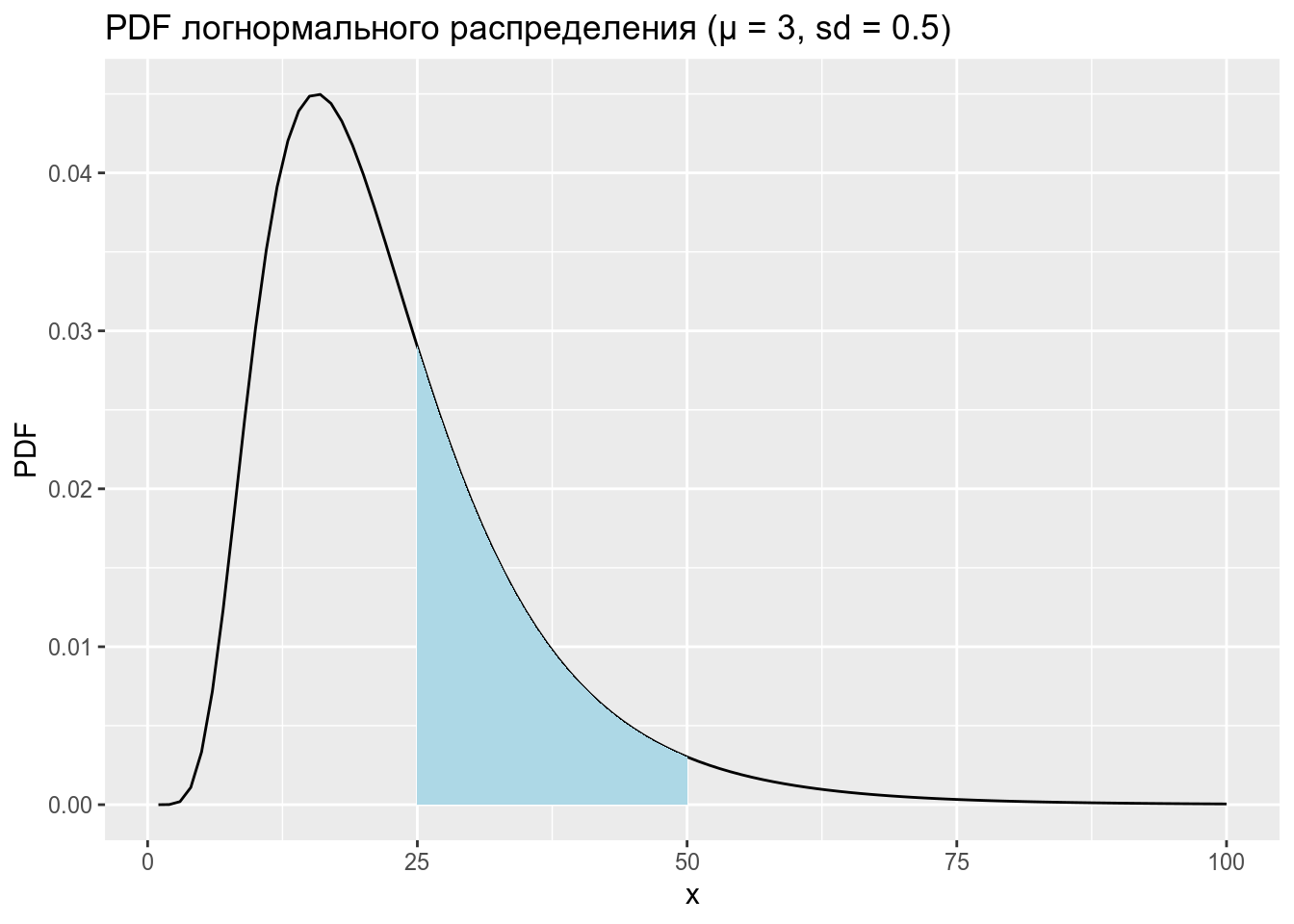
1.2
Дан график логнормального распределения со средним 3 и стандартным отклонением 0.5. Используйте функцию integrate, чтобы посчитать закрашенную площадь под кривой.