2. Байесовский статистический вывод
Г. Мороз
1. Формула Байеса
\[p(A|B) = \frac{p(A, B)}{p(B)}\Rightarrow p(A|B) \times p(B) = p(A, B)\] \[p(B|A) = \frac{p(B, A)}{p(A)}\Rightarrow p(B|A) \times p(A) = p(B, A)\] \[p(A|B) \times p(B) = p(B|A) \times p(A)\] \[p(A|B) = \frac{p(B|A)p(A)}{p(B)}\]
Discrete case: \[p(A|B) = \frac{p(B|A)p(A)}{\sum_{i=1}^{n} p(B, a_i) \times p(a_i)}\]
Continuouse case: \[p(A|B) = \frac{p(B|A)p(A)}{\int p(B, a) \times p(a)da}\]
Некоторым помогает вот такое объяснение:
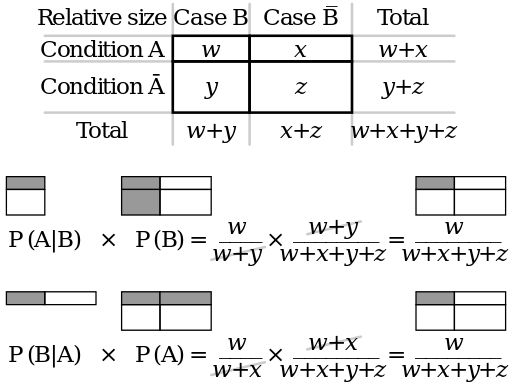
2. Байесовский статистический вывод
В байесовском подоходе статистический вывод описывается формулой Байеса
\[P(θ|Data) = \frac{P(Data|θ)\times P(θ)}{P(Data)}\]
- \(P(θ|Data)\) — апостериорная вероятность (posterior)
- \(P(Data|θ)\) — функция правдоподобия (likelihood)
- \(P(θ)\) — априорная вероятность (prior)
- \(P(Data)\) — нормализующий делитель
В литературе можно еще встретить такую нотацию:
\[P(θ|Data) \propto P(Data|θ)\times P(θ)\]
3. Сопряженные распределения (сonjugate priors)
Если у нас есть некоторые данные с функцией правдоподобия P(Data|θ), а априорное и апостериорное распределения θ относятся к одному семейству распределений, то данное семейство распредлений называется сопряжённым априорным распределением к функции правдоподобия P(Data|θ) (conjugate prior).
3.1 Бета распределение
\[P(x; α, β) = \frac{x^{α-1}\times (1-x)^{β-1}}{B(α, β)}; 0 \leq x \leq 1; α, β > 0\]
Бета функция:
\[Β(α, β) = \frac{Γ(α)\times Γ(β)}{Γ(α+β)} = \frac{(α-1)!(β-1)!}{(α+β-1)!} \]
\[\mu = \frac{\alpha}{\alpha+\beta}\]
\[\sigma = \frac{\alpha\times\beta}{(\alpha+\beta)^2\times(\alpha+\beta+1)}\]
Если кому-то захочется построить бета распределение самостоятельно:
data_frame(x = seq(0, 1, length = 100),
density = dbeta(x, shape1 = 5, shape2 = 10)) %>%
ggplot(aes(x, density))+
geom_line()+
ggtitle("Бета распределение с параметрами α - 5 и β - 10")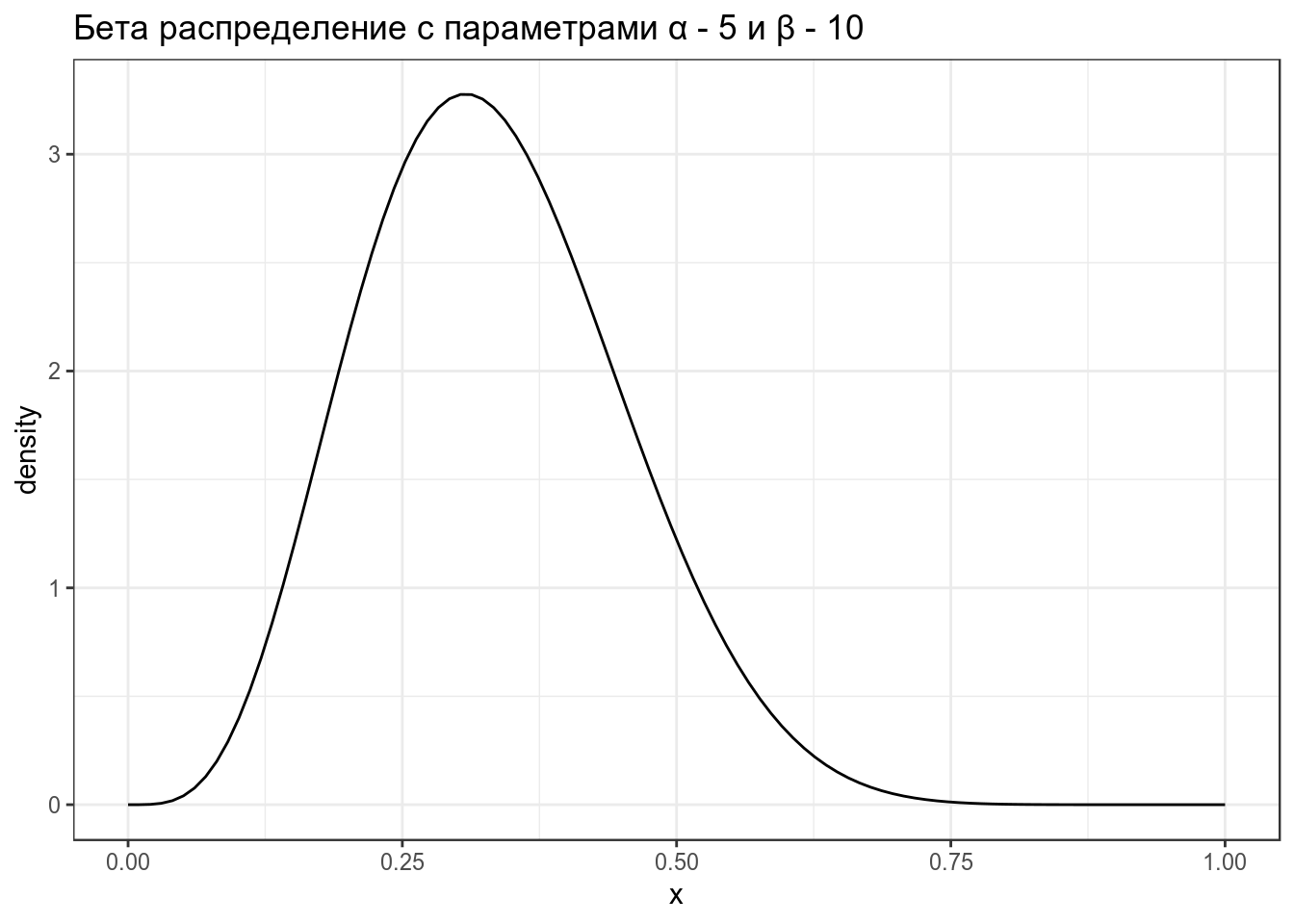
3.2 Нормальное распределение
3.3 Другие сопряженные распределения…
… перечислены на этой страниц.
4. Байесовский вывод
4.1 Биномиальные данные
\[Beta_{post}(\alpha_{post}, \beta_{post}) = Beta(\alpha_{prior}+\alpha_{data}, \beta_{prior}+\beta_{data}),\] где \(Beta\) — это бета распределение
Подробнее см.:
- 2 главу Robinson D. (2017) Introduction To Empirical Bayes
- раздел 2.5 в Gelman A. et. al (2014) Bayesian Data Analysis
4.2 Нормально распределенные данные с известной дисперсией
Начнем с апостериорных параметров для наблюдений \(x_1, ... x_n\) со средним \(\mu_{data}\) известной дисперсией \(\sigma_{known}^2\)
\[\sigma_{post}^2=(\frac{1}{\sigma_{prior}^2}+\frac{n}{\sigma_{known}^2})^{-1}\]
\[\mu_{post} = \sigma^2_{post}\times\left(\frac{\mu_{prior}}{\sigma_{prior}^2}+\frac{n\times\mu_{data}}{\sigma_{known}^2}\right)\]
\(\frac{1}{\sigma}\) часто называют точностью (precision) и обозначают \(\tau\), тогда полученные показатели имеют форму
\[\tau_{post}^2=\tau_{prior}^2+n\times\tau_{known}^2\]
\[\mu_{post} = \frac{\mu_{prior}\times\tau_{prior}^2+n\times\bar x\times\tau_{known}^2}{\tau_{post}^2} \]
Подробнее см.:
- Murphy K. P. (2007) Conjugate Bayesian analysis of the Gaussian distribution
- Jordan M. I. (2010) The Conjugate Prior for the Normal Distribution
- раздел 2.5 в Gelman A. et. al (2014) Bayesian Data Analysis
Домашнее задание (до 19.12.2018)
- Вспомнить про доверительные интервалы.
Домашнее задание (до 26.12.2018)
Домашнее задание нужно выполнять в отдельном rmarkdown файле. Получившийся файл следует помещать в соответствующую папку в своем репозитории на гитхабе. Более подробные инструкции см. на этой странице.
В этой домашней работе я предлагаю поработать с поддатасетом данных из базы данных Phoible, в которой собраны фонологические инвентари в языках мира. В каждый набор данных записано всего три переменных:
language— язык;consonants— количество согласных;phonemes— количество фонем.
Я предлагаю исследовать долю, которую согласные составляют от всего фонологического набора.
2.1
Посчитайте долю, которую составляет согласные от всего фонологического набора каждого языка и выведите в консоль название языка, в котором эта доля максимальна
2.2
Проведите байесовский апдейт наблюдений каждого языка, используя в качестве априорного распределения бета распределение с параметрами α = 9.300246, и β = 4.4545. Посчитайте модуль разницы между апостериорной долей и изначальной долей представленной в данных. В консоль выведите 6 языков с наибольшей разницей.
