18 Методы уменьшения размерностей
Методы уменьшения размерностей – это эксплораторные методы, которые позволяет использовать меньше переменных для того, чтобы найти связи в данных и связи между переменными. Немножко жаргона: размерность здесь является прямым аналогом размерности в описании физических объектов (например, 2-ухмерное, 3-ехмерное, 4-ехмерное и т. д. пространство). Важно понимать, что каждая переменная в любом датасете можно воспринимать как отдельную размерность, так что каждая строчка в датасете mtcars – объект в 11-мерном пространстве просто потому что в этом датасете 11 переменных.
18.1 Визуализация многомерных пространств
Визуализация многомерного пространства — дело сложное. Когда переменных не так уж и много, то в целом данную задачу можно решить используя разные трюки:
- много диаграмм рассеяния
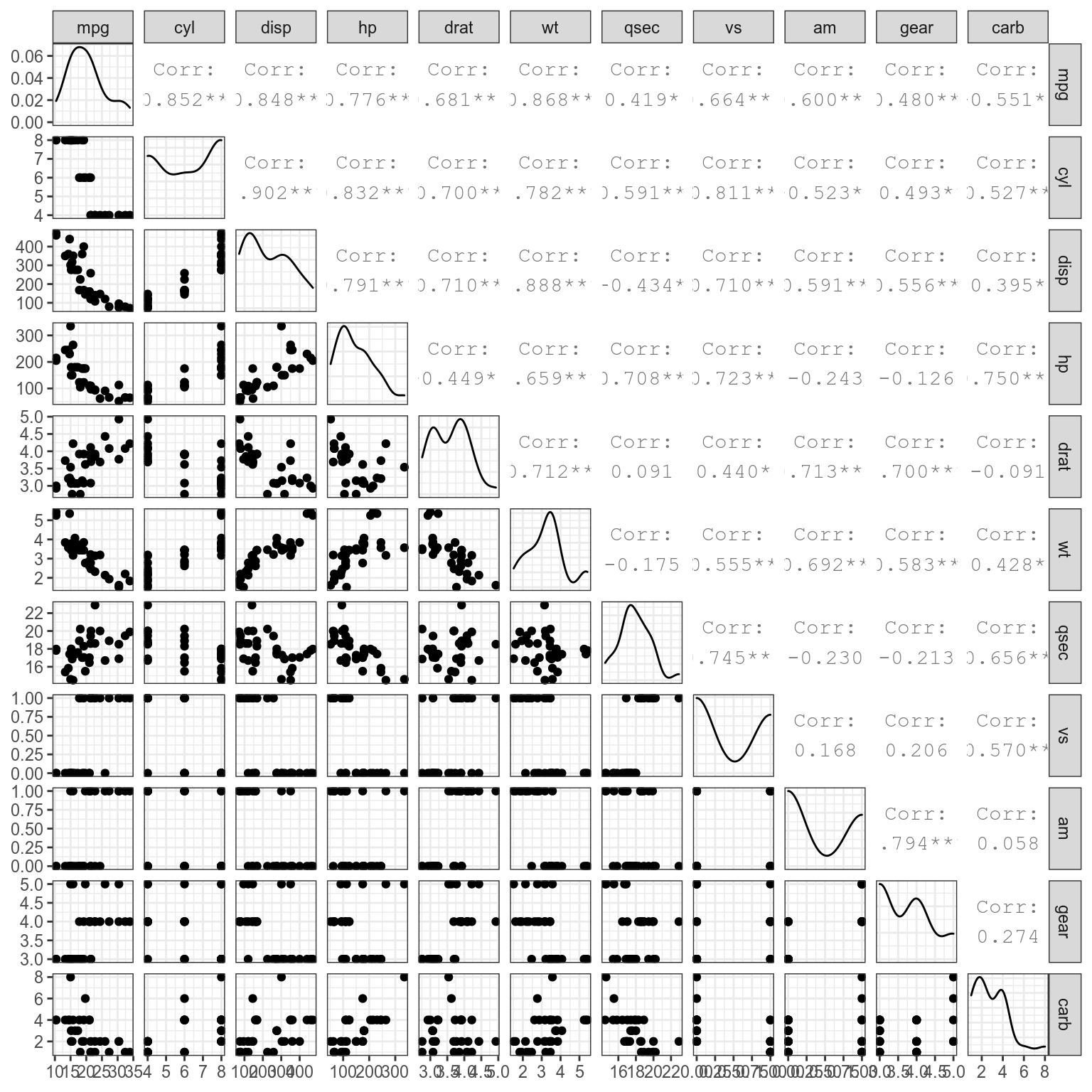
- радиальная диаграмма (радар, паук)
mtcars %>%
mutate(car_names = rownames(mtcars)) %>%
pivot_longer(names_to = "variables", values_to = "values", mpg:carb) %>%
mutate(variables = factor(variables, levels = colnames(mtcars))) %>%
ggplot(aes(variables, values, color = car_names, group = car_names))+
geom_point()+
geom_polygon(fill = NA)+
ggproto("CordRadar", CoordPolar, theta = "x", r = "x", start = 0, direction = 1, is_linear = function(coord) TRUE)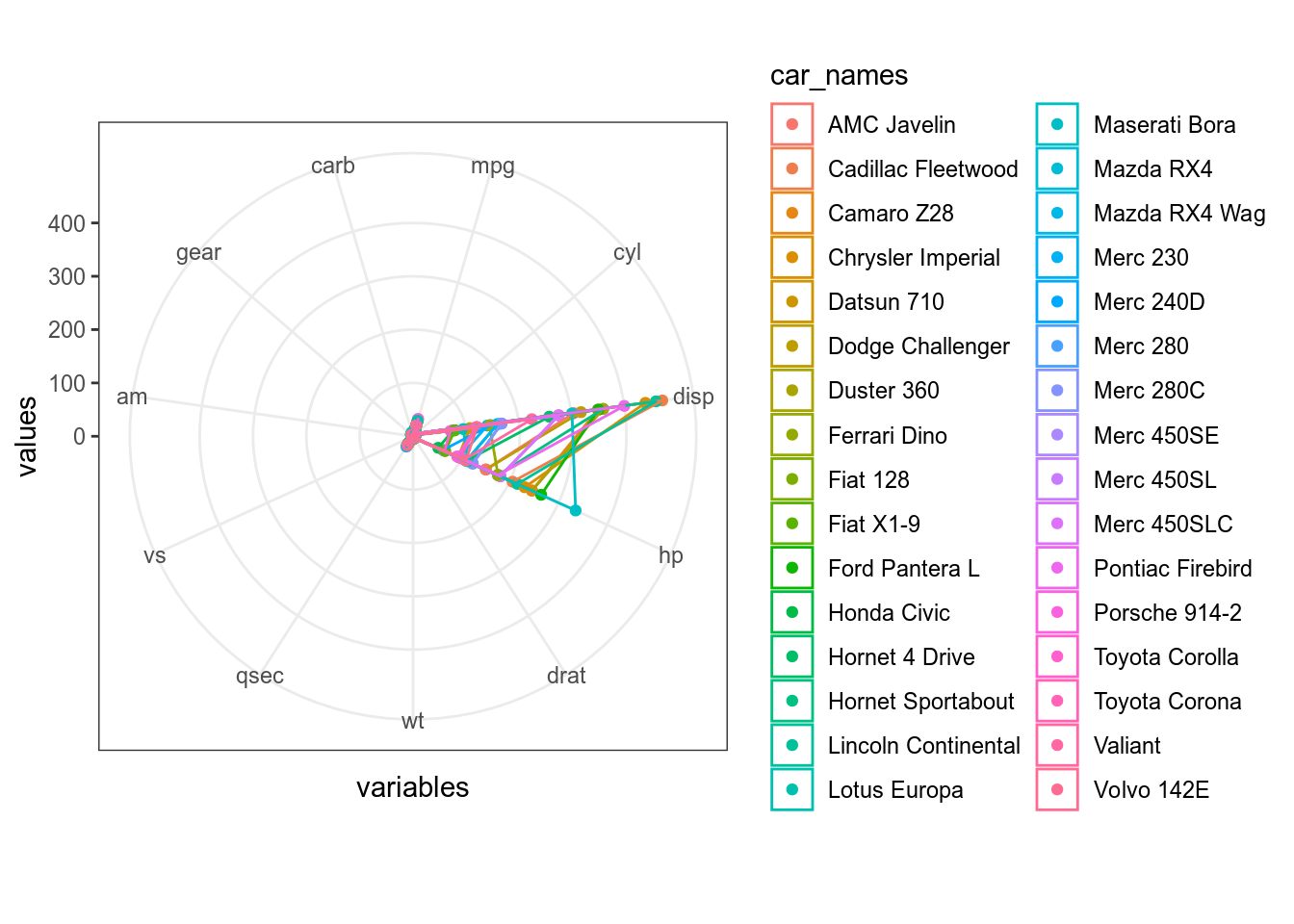
Не очень видно. Давайте нормализуем переменные:
mtcars %>%
mutate_all(scale) %>%
mutate(car_names = rownames(mtcars)) %>%
pivot_longer(names_to = "variables", values_to = "values", mpg:carb) %>%
mutate(variables = factor(variables, levels = colnames(mtcars))) %>%
ggplot(aes(variables, values, color = car_names, group = car_names))+
geom_point()+
geom_polygon(fill = NA)+
ggproto("CordRadar", CoordPolar, theta = "x", r = "x", start = 0, direction = 1, is_linear = function(coord) TRUE)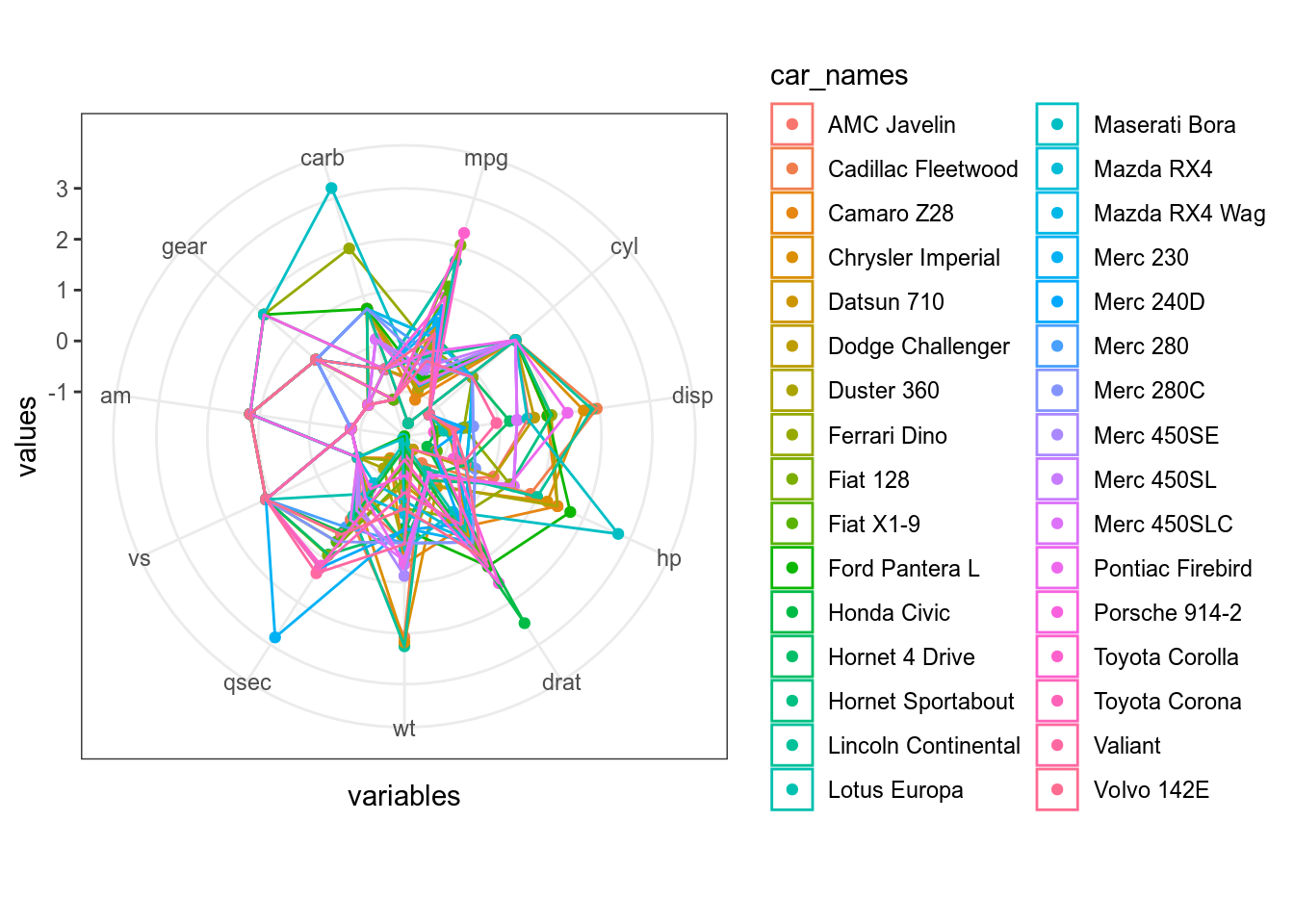
Все равно не очень хорошо видно, давайте сделаем фасетизацию:
mtcars %>%
mutate_all(scale) %>%
mutate(car_names = rownames(mtcars)) %>%
pivot_longer(names_to = "variables", values_to = "values", mpg:carb) %>%
mutate(variables = factor(variables, levels = colnames(mtcars))) %>%
ggplot(aes(variables, values, group = car_names, color = car_names))+
geom_point(show.legend = FALSE)+
geom_polygon(fill = NA, show.legend = FALSE)+
facet_wrap(~car_names)+
ggproto("CordRadar", CoordPolar, theta = "x", r = "x", start = 0, direction = 1, is_linear = function(coord) TRUE)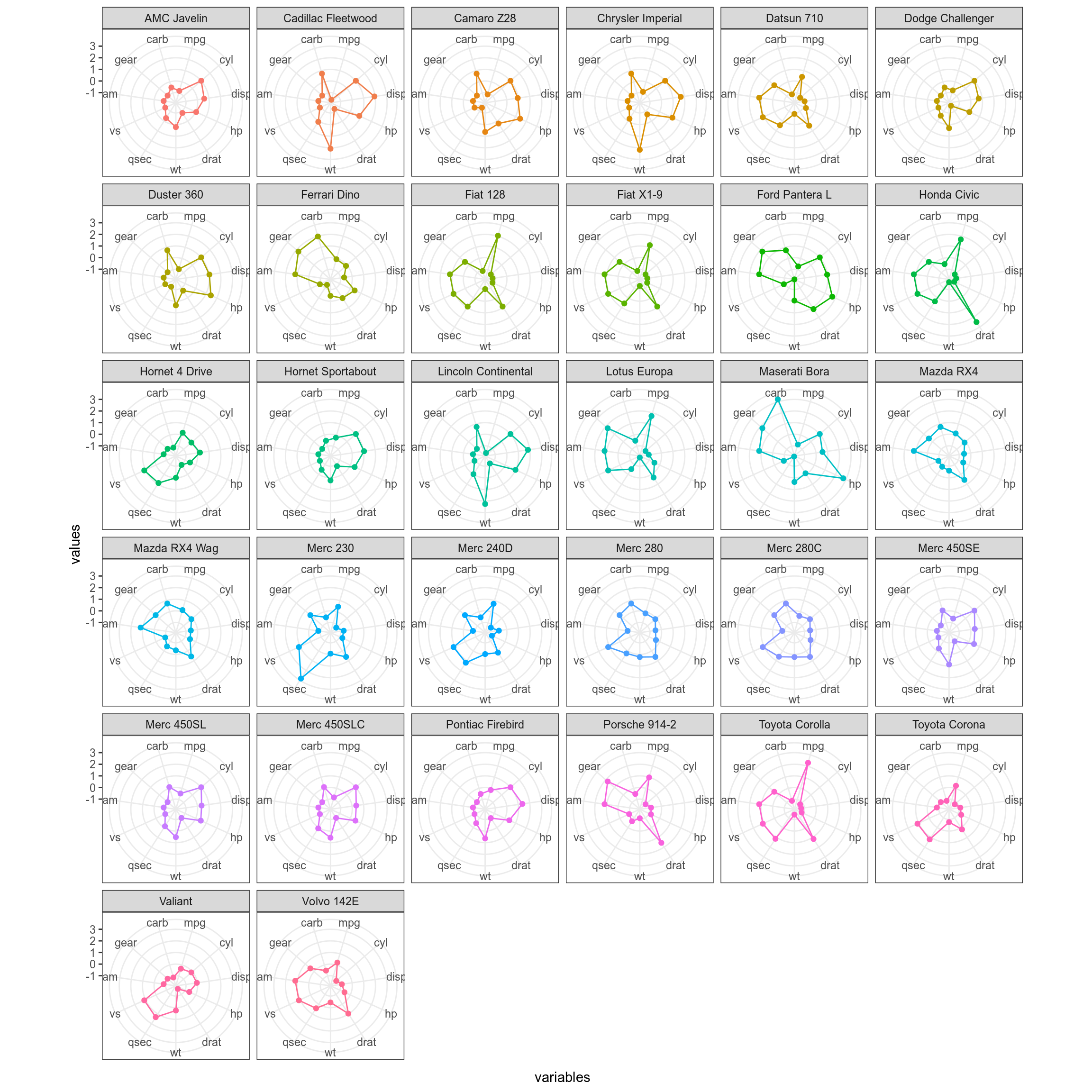
18.2 Простой пример: из двумерного пространства в одномерное пространство
Мы уже рассматривали связь между количество слов в рассказе и количеством слов и в рассказах М. Зощенко:
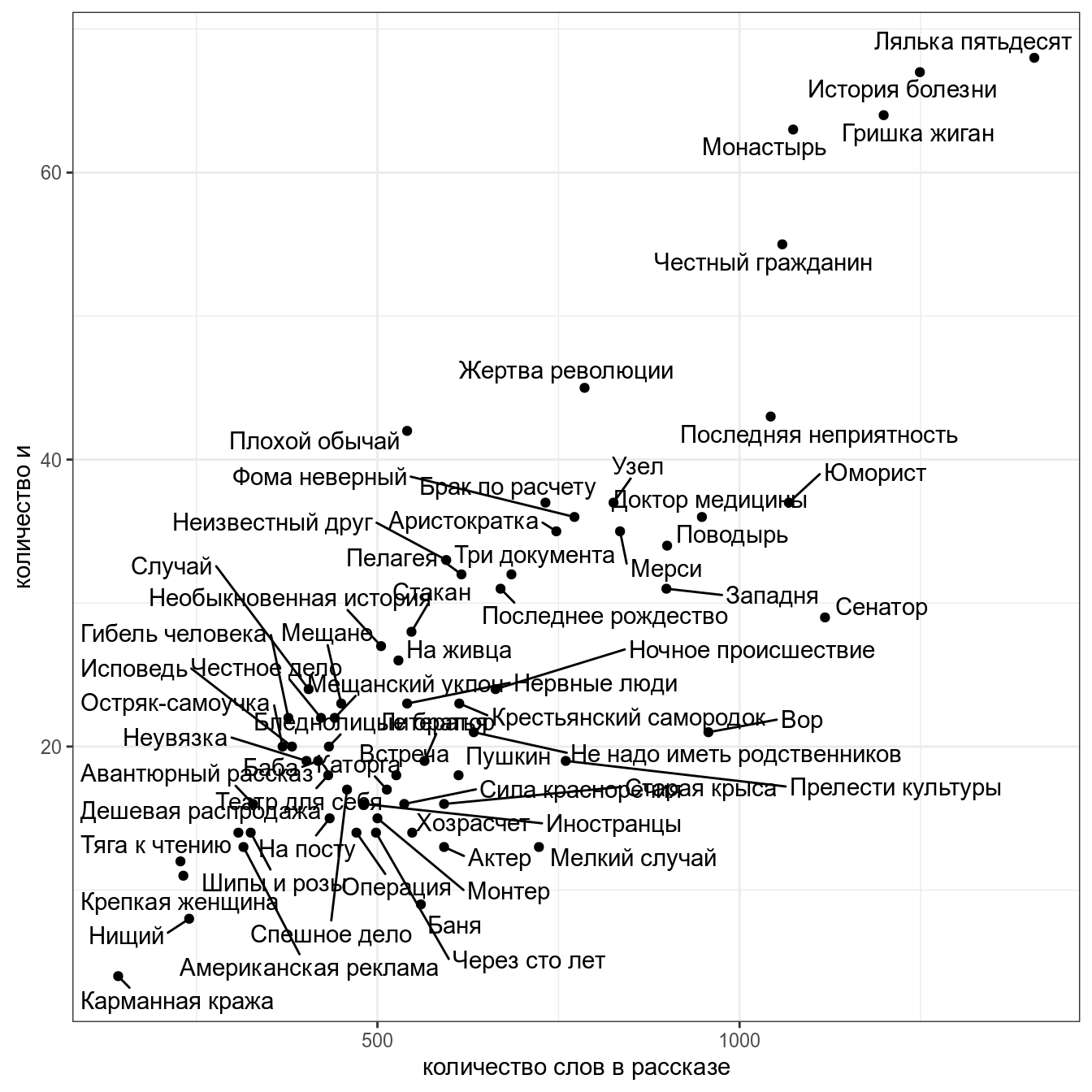
Мы уже смотрели коэффициент корреляции между этими переменными (r = 0.83).
Представим, что я перешел к новой системе координат:
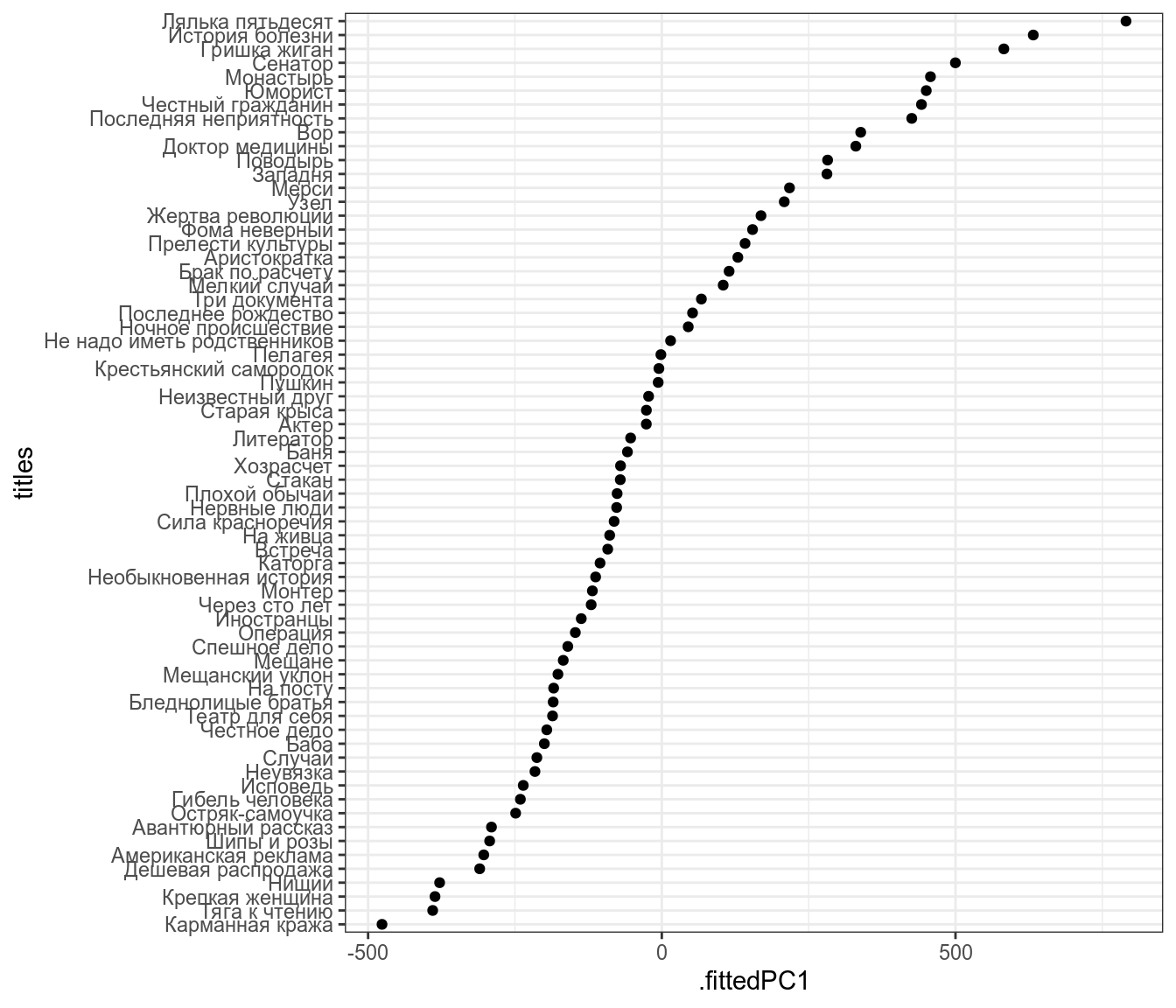
Теперь я могу предсказывать значения переменных количество слов в рассказе и количестов и в рассказе на основе этой новой переменной.
zo %>%
select(n, n_words) %>%
prcomp(scale. = TRUE) %>%
broom::augment(zo) %>%
pivot_longer(names_to = "type", values_to = "value", n:n_words) %>%
mutate(type = recode(type, n = "количество и", n_words = "количество слов")) %>%
group_by(type) %>%
mutate(cor = str_c("r = ",round(cor(.fittedPC1, value), 2)),
max = max(value)- sd(value)) %>%
ggplot(aes(.fittedPC1, value))+
geom_point()+
geom_label(aes(label = cor, y = max), x = -1.5)+
facet_wrap(~type, scales = "free")+
labs(x = "новая переменная", y = "старые переменные")
18.3 Многомерное шкалирование (MDS)
Многомерное шкалирование – преобразование из многомерного пространства в n-мерное пространство (чаще всего смотрят на n равное 2), которое старается как можно меньше исказить расстояния между наблюдениями.
iris %>%
select(-Species) %>%
dist() %>%
cmdscale() %>%
as_tibble() %>%
bind_cols(iris) %>%
ggplot(aes(V1, V2, color = Species))+
geom_point()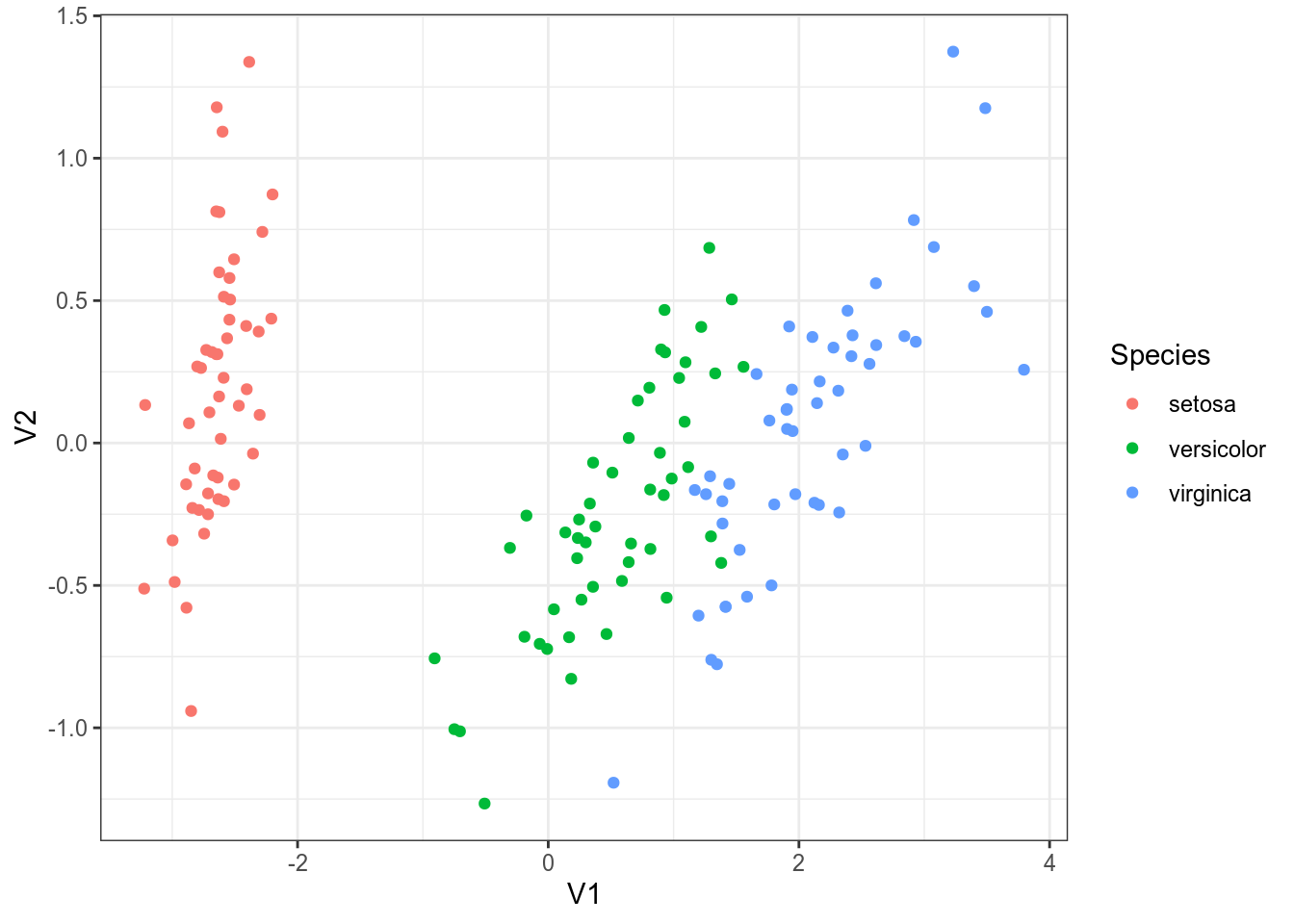
Если по какой-то причине вы хотите использовать большую размерность итогового пространства, можно использовать аргумент k функции cmdscale() (по умолчанию он 2). Как видно из кода, я использовал функцию dist(), которую мы видели в предыдущем разделе: мы можем использовать любую другую матрицу расстояний, которую мы посчитаем (существует множество метрик расстояния, которые можно посмотреть в справке ?dist). Давайте, например, посмотрим на многомерное шкалирование расстояний Левинштейна-Димерау между стопсловами русского языка:
library(stringdist)
library(stopwords)
stringdistmatrix(stopwords("ru")) %>%
cmdscale() %>%
as_tibble() %>%
mutate(words = stopwords("ru")) %>%
ggplot(aes(V1, V2, label = words))+
geom_text()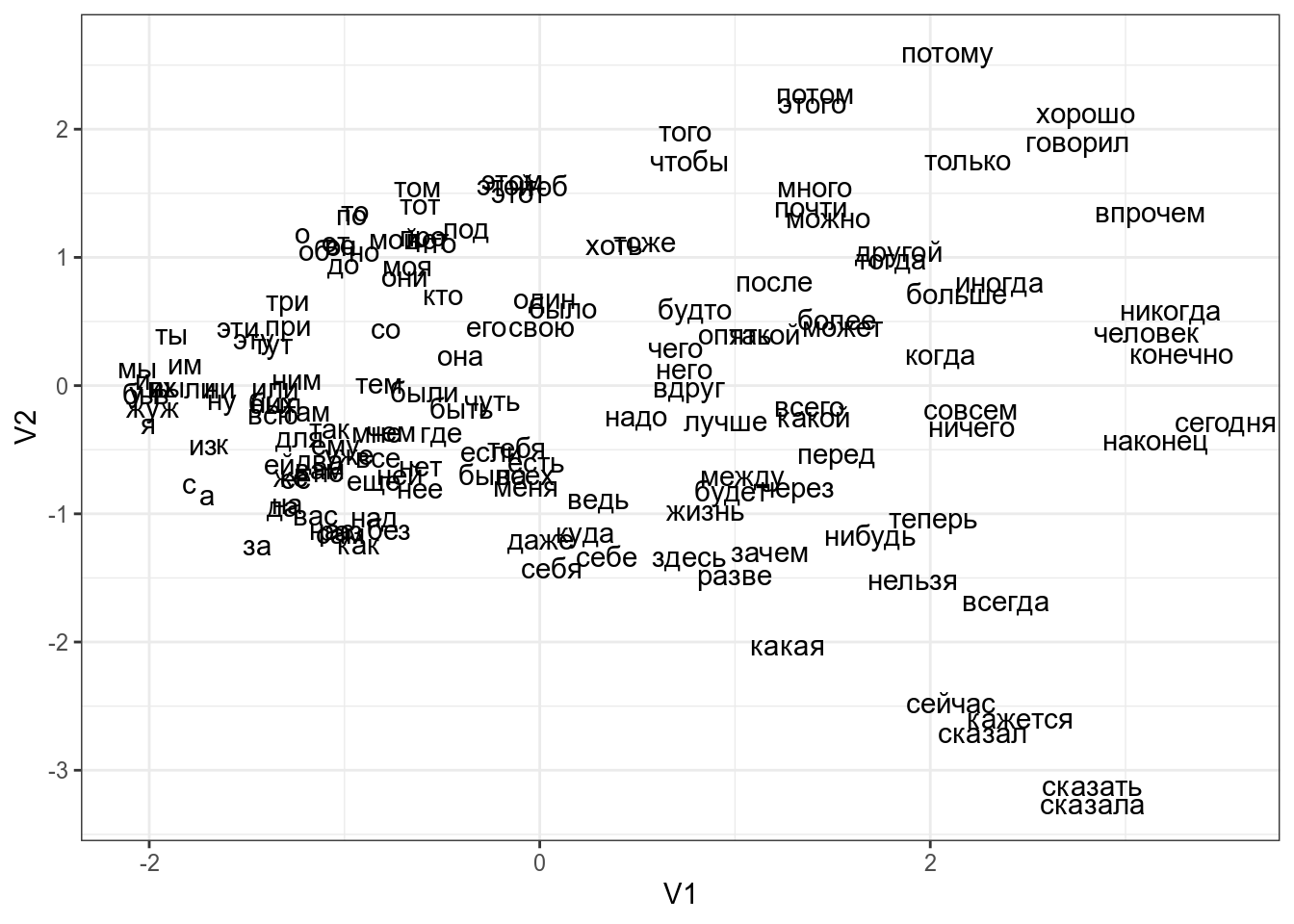
Как интерпретировать получившийся график? Часто мы не можем придать никакого значения получившимся осям, однако расстояния между точками на графике призвано отражать расстояние в многомерном пространстве. Так что, используя многомерное шкалирование
- можно обнаружить, есть ли кластеры в многомерных данных
- можно обнаружить, есть ли связь между наблюдениями, в том числе невыраженная переменными, которые есть в датасете. Например, из графика со стопсловами, видна “скрытая” переменная – длина слова.
В датасет записаны частотности некоторых слов в рассказах А. Чехова и М. Зощенко. Постройте многомерное шкалирование используя все переменные, и раскрасьте рассказы в зависимости от авторства. Делятся ли рассказы на кластеры? Как вы думаете почему?
18.4 Метод главных компонент (PCA)
Метод главных компонент – преобразование из многомерного пространства в n-мерное пространство (чаще всего смотрят на n равное 2), которое старается как можно меньше исказить корреляции между переменными.
library(broom)
iris %>%
select(-Species) %>%
prcomp() %>%
augment(iris) %>%
ggplot(aes(.fittedPC1, .fittedPC2, color = Species))+
geom_point()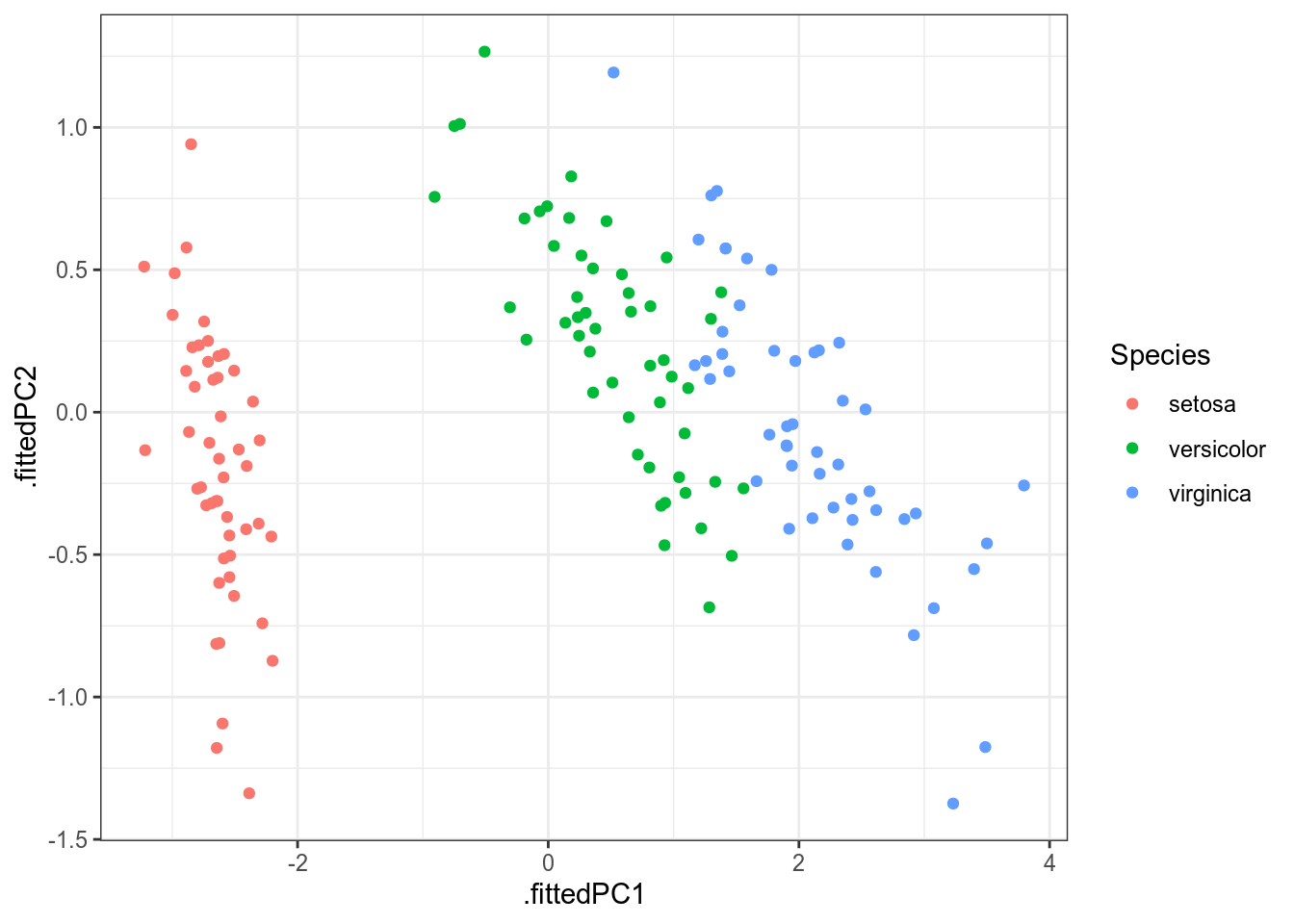
В целом, эта картинка ничем не отличается от полученной нам в многомерном шкалировании (плсю-минус зеркальное отображение; так будет каждый раз, если при построении многомерного шкалирования использовано евклидово расстояние).
Так как метод главных компонент старается сохранить как можно больше дисперсии из всех данных, в результате этот метод (да и многомерное шкалирование) очень чувствителен к дисперсии переменных. Это значит, что данный метод будет давать разные результаты в зависимости того, в метрах исследуемая переменная или в километрах. Чтобы предотвратить этот крен в сторону переменных с большей дисперсией, следует добавлять в функцию prcomp() аргумент scale. = TRUE, которые, соответственно нормализует переменные перед применением алгоритма:
iris %>%
select(-Species) %>%
prcomp(scale. = TRUE) %>%
augment(iris) %>%
ggplot(aes(.fittedPC1, .fittedPC2, color = Species))+
geom_point()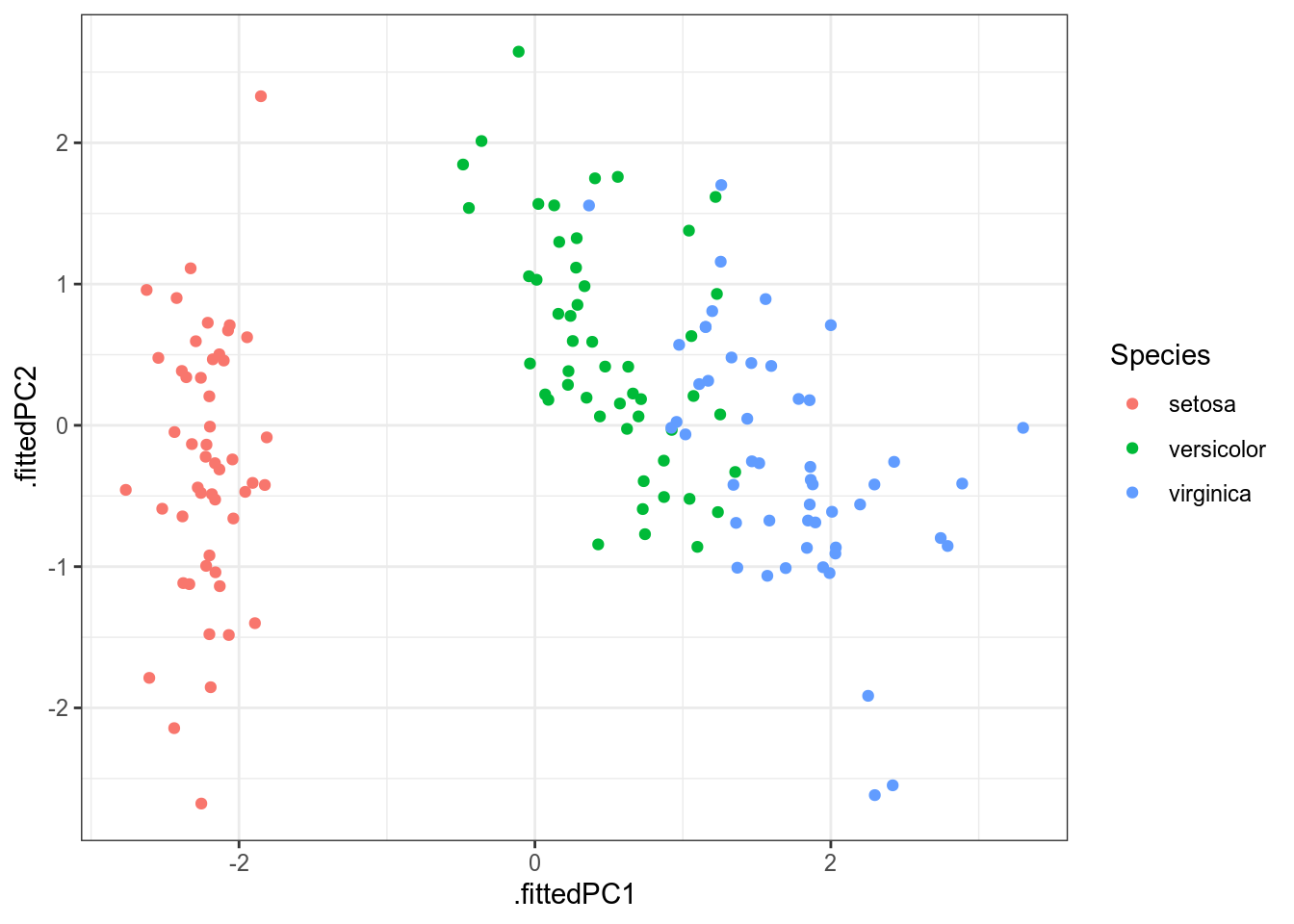
В отличие от многомерного шкалирования, метод главных компонент позволяет также посмотреть на процент объясненной дисперсии:
Importance of components:
PC1 PC2 PC3 PC4
Standard deviation 1.7084 0.9560 0.38309 0.14393
Proportion of Variance 0.7296 0.2285 0.03669 0.00518
Cumulative Proportion 0.7296 0.9581 0.99482 1.00000Ученые (к счастью) не договорились относительно порога, начиная с которого процент объясненной дисперсии является хорошим. Я обычно радуюсь значением больше 0.7 (т. е. при переходе к новым осям мы выкинули всего 30% дисперсии).
Кроме того, благодаря методу главных компонент мы можем посмотреть на связь переменных. Давайте продемонстрируем это на частотности слов в евангелиях:
gospels <- read_csv("https://raw.githubusercontent.com/agricolamz/2019_data_analysis_for_linguists/master/data/gospel_freq_words.csv")Parsed with column specification:
cols(
word = col_character(),
John = col_double(),
Luke = col_double(),
Mark = col_double(),
Matthew = col_double()
)PCA <- prcomp(gospels[,-1], scale. = TRUE)
row.names(PCA$x) <- gospels$word
library(ggfortify)
autoplot(PCA,
shape = FALSE,
loadings = TRUE,
label = TRUE,
loadings.label = TRUE)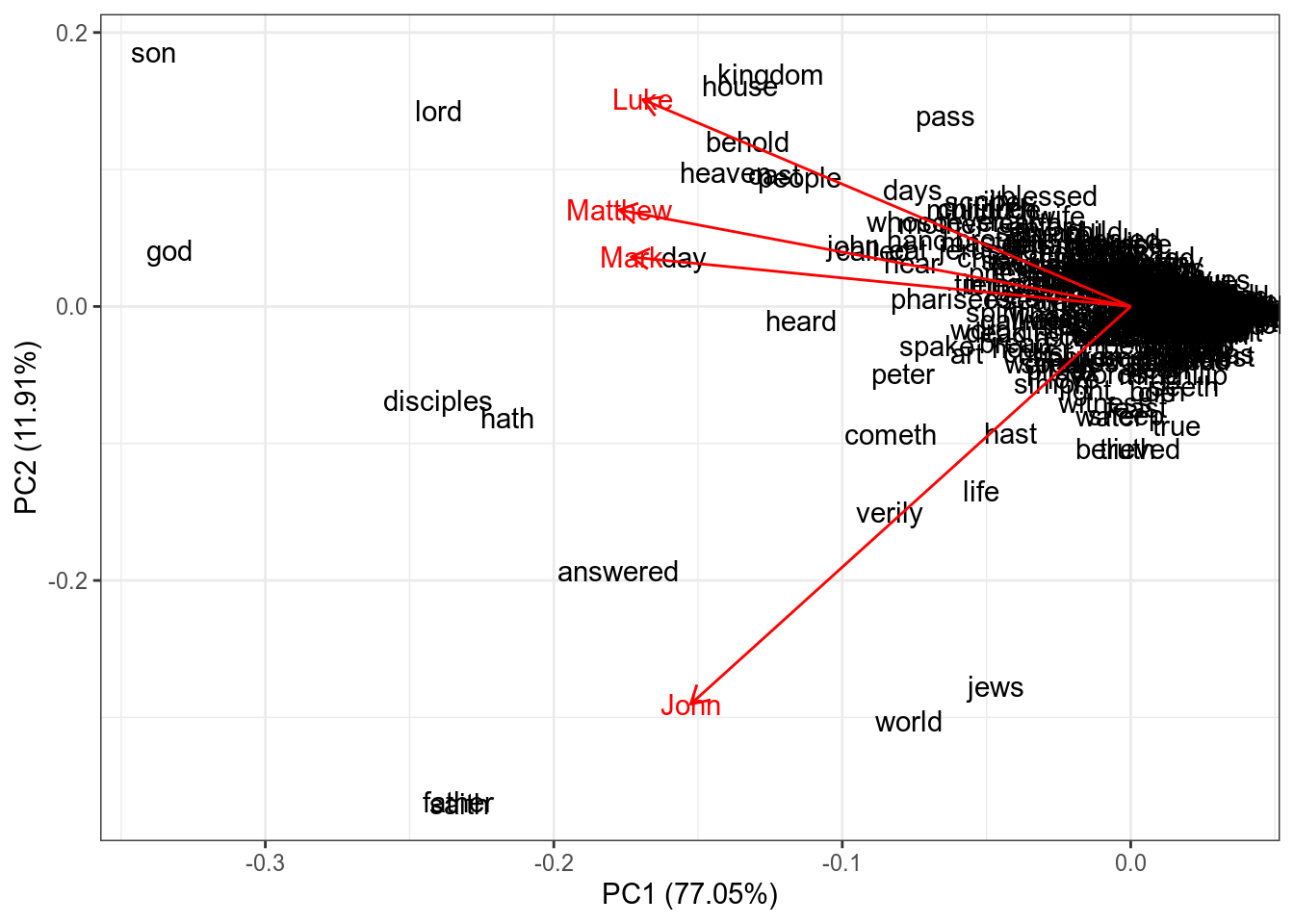
Косинус угла между стрелочками соответствует коэффиценту корреляции между ними
John Luke Mark Matthew
John 1.0000000 0.5560482 0.6357893 0.6397344
Luke 0.5560482 1.0000000 0.7277001 0.7962913
Mark 0.6357893 0.7277001 1.0000000 0.7916982
Matthew 0.6397344 0.7962913 0.7916982 1.0000000Мы точно так же можем работать не только с данными, но и с матрицей расстояния:
st_words <- tibble(words = stopwords("ru"))
stringdistmatrix(st_words$words) %>%
prcomp(scale. = TRUE) %>%
augment(st_words) %>%
ggplot(aes(.fittedPC1, .fittedPC2, label = words))+
geom_text()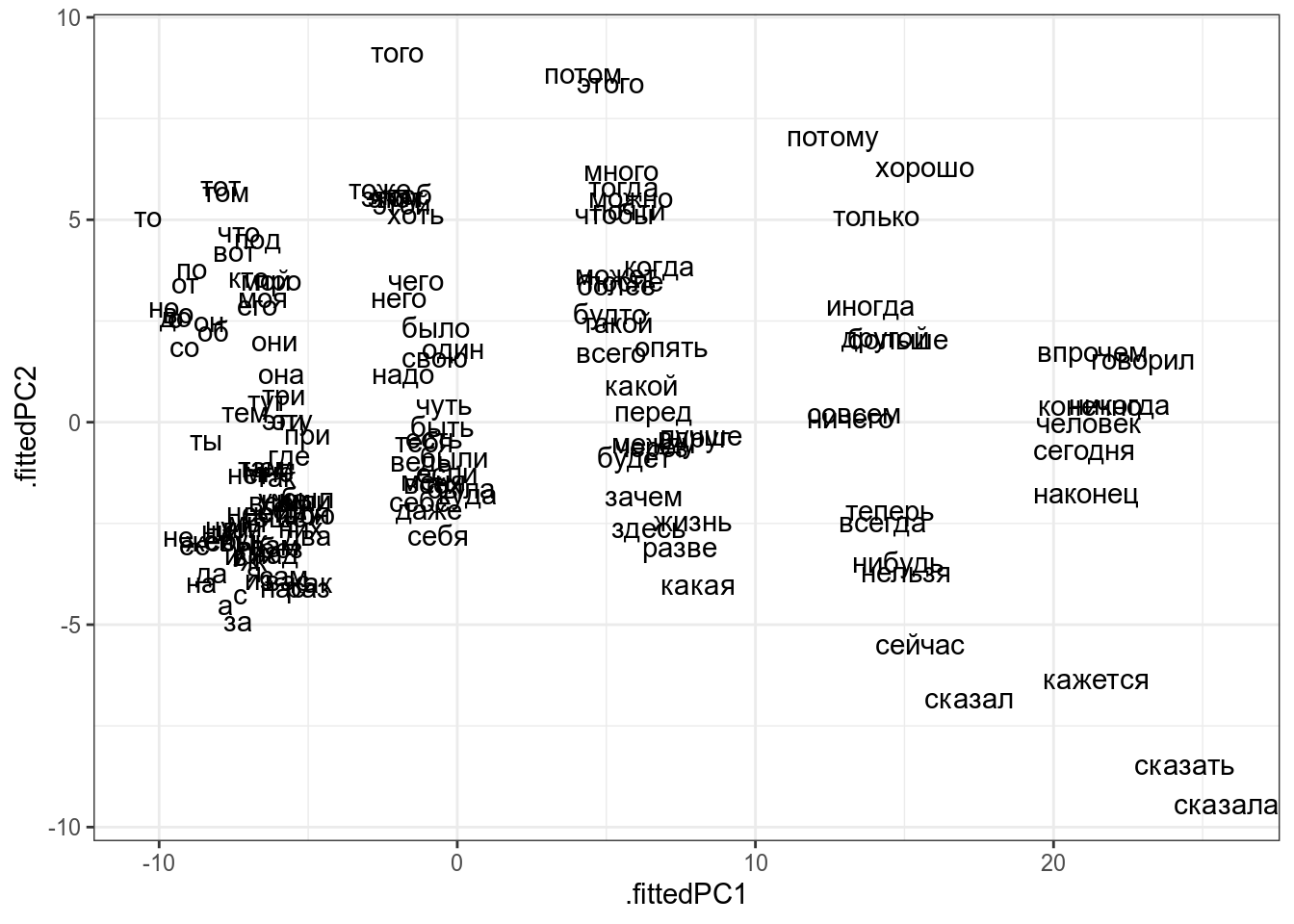
Importance of components:
PC1 PC2 PC3 PC4 PC5 PC6 PC7
Standard deviation 9.1094 3.50931 3.05332 2.5126 2.40159 2.20270 2.10269
Proportion of Variance 0.5219 0.07745 0.05863 0.0397 0.03627 0.03051 0.02781
Cumulative Proportion 0.5219 0.59935 0.65798 0.6977 0.73396 0.76448 0.79228
PC8 PC9 PC10 PC11 PC12 PC13 PC14
Standard deviation 1.83939 1.68455 1.64582 1.50108 1.43699 1.32001 1.19788
Proportion of Variance 0.02128 0.01785 0.01704 0.01417 0.01299 0.01096 0.00902
Cumulative Proportion 0.81356 0.83141 0.84844 0.86262 0.87560 0.88656 0.89559
PC15 PC16 PC17 PC18 PC19 PC20 PC21
Standard deviation 1.14934 1.12332 1.08208 1.04435 0.93055 0.90376 0.88367
Proportion of Variance 0.00831 0.00794 0.00736 0.00686 0.00545 0.00514 0.00491
Cumulative Proportion 0.90389 0.91183 0.91919 0.92605 0.93150 0.93664 0.94155
PC22 PC23 PC24 PC25 PC26 PC27 PC28
Standard deviation 0.87275 0.81203 0.75994 0.73676 0.7249 0.67007 0.64885
Proportion of Variance 0.00479 0.00415 0.00363 0.00341 0.0033 0.00282 0.00265
Cumulative Proportion 0.94634 0.95049 0.95412 0.95753 0.9608 0.96366 0.96631
PC29 PC30 PC31 PC32 PC33 PC34 PC35
Standard deviation 0.61520 0.59373 0.5775 0.57012 0.53217 0.5039 0.48679
Proportion of Variance 0.00238 0.00222 0.0021 0.00204 0.00178 0.0016 0.00149
Cumulative Proportion 0.96869 0.97091 0.9730 0.97505 0.97683 0.9784 0.97992
PC36 PC37 PC38 PC39 PC40 PC41 PC42
Standard deviation 0.48309 0.44708 0.43207 0.3987 0.39240 0.36516 0.35923
Proportion of Variance 0.00147 0.00126 0.00117 0.0010 0.00097 0.00084 0.00081
Cumulative Proportion 0.98138 0.98264 0.98381 0.9848 0.98578 0.98662 0.98743
PC43 PC44 PC45 PC46 PC47 PC48 PC49
Standard deviation 0.34764 0.3330 0.31735 0.31360 0.30236 0.29669 0.28040
Proportion of Variance 0.00076 0.0007 0.00063 0.00062 0.00057 0.00055 0.00049
Cumulative Proportion 0.98819 0.9889 0.98952 0.99014 0.99072 0.99127 0.99177
PC50 PC51 PC52 PC53 PC54 PC55 PC56
Standard deviation 0.27511 0.26238 0.24448 0.23832 0.23560 0.22759 0.22533
Proportion of Variance 0.00048 0.00043 0.00038 0.00036 0.00035 0.00033 0.00032
Cumulative Proportion 0.99224 0.99267 0.99305 0.99341 0.99376 0.99408 0.99440
PC57 PC58 PC59 PC60 PC61 PC62 PC63
Standard deviation 0.22146 0.21053 0.20631 0.20455 0.20016 0.19190 0.18747
Proportion of Variance 0.00031 0.00028 0.00027 0.00026 0.00025 0.00023 0.00022
Cumulative Proportion 0.99471 0.99499 0.99526 0.99552 0.99577 0.99600 0.99622
PC64 PC65 PC66 PC67 PC68 PC69 PC70
Standard deviation 0.18245 0.1775 0.16788 0.16499 0.16281 0.15790 0.15292
Proportion of Variance 0.00021 0.0002 0.00018 0.00017 0.00017 0.00016 0.00015
Cumulative Proportion 0.99643 0.9966 0.99681 0.99698 0.99715 0.99730 0.99745
PC71 PC72 PC73 PC74 PC75 PC76 PC77
Standard deviation 0.14735 0.14341 0.13953 0.13850 0.13316 0.12972 0.1273
Proportion of Variance 0.00014 0.00013 0.00012 0.00012 0.00011 0.00011 0.0001
Cumulative Proportion 0.99759 0.99772 0.99784 0.99796 0.99807 0.99818 0.9983
PC78 PC79 PC80 PC81 PC82 PC83 PC84
Standard deviation 0.1260 0.1247 0.11829 0.11670 0.11507 0.10871 0.10524
Proportion of Variance 0.0001 0.0001 0.00009 0.00009 0.00008 0.00007 0.00007
Cumulative Proportion 0.9984 0.9985 0.99857 0.99865 0.99873 0.99881 0.99888
PC85 PC86 PC87 PC88 PC89 PC90 PC91
Standard deviation 0.10464 0.10307 0.10104 0.09898 0.09473 0.09188 0.08819
Proportion of Variance 0.00007 0.00007 0.00006 0.00006 0.00006 0.00005 0.00005
Cumulative Proportion 0.99895 0.99901 0.99908 0.99914 0.99920 0.99925 0.99930
PC92 PC93 PC94 PC95 PC96 PC97 PC98
Standard deviation 0.08491 0.08265 0.07868 0.07556 0.07372 0.07262 0.07084
Proportion of Variance 0.00005 0.00004 0.00004 0.00004 0.00003 0.00003 0.00003
Cumulative Proportion 0.99934 0.99939 0.99943 0.99946 0.99950 0.99953 0.99956
PC99 PC100 PC101 PC102 PC103 PC104 PC105
Standard deviation 0.06751 0.06516 0.06446 0.06293 0.05934 0.05823 0.05722
Proportion of Variance 0.00003 0.00003 0.00003 0.00002 0.00002 0.00002 0.00002
Cumulative Proportion 0.99959 0.99962 0.99964 0.99967 0.99969 0.99971 0.99973
PC106 PC107 PC108 PC109 PC110 PC111 PC112
Standard deviation 0.05516 0.05259 0.05088 0.04966 0.04914 0.04855 0.04592
Proportion of Variance 0.00002 0.00002 0.00002 0.00002 0.00002 0.00001 0.00001
Cumulative Proportion 0.99975 0.99977 0.99978 0.99980 0.99981 0.99983 0.99984
PC113 PC114 PC115 PC116 PC117 PC118 PC119
Standard deviation 0.04558 0.04354 0.04276 0.04101 0.03932 0.03791 0.03683
Proportion of Variance 0.00001 0.00001 0.00001 0.00001 0.00001 0.00001 0.00001
Cumulative Proportion 0.99986 0.99987 0.99988 0.99989 0.99990 0.99991 0.99992
PC120 PC121 PC122 PC123 PC124 PC125 PC126
Standard deviation 0.03536 0.03501 0.03392 0.03064 0.03019 0.02806 0.027
Proportion of Variance 0.00001 0.00001 0.00001 0.00001 0.00001 0.00000 0.000
Cumulative Proportion 0.99992 0.99993 0.99994 0.99995 0.99995 0.99996 1.000
PC127 PC128 PC129 PC130 PC131 PC132 PC133
Standard deviation 0.02557 0.02505 0.02465 0.02362 0.02252 0.02098 0.01907
Proportion of Variance 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000
Cumulative Proportion 0.99997 0.99997 0.99997 0.99998 0.99998 0.99998 0.99998
PC134 PC135 PC136 PC137 PC138 PC139 PC140
Standard deviation 0.01786 0.01688 0.01635 0.01546 0.01501 0.01397 0.01348
Proportion of Variance 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000 0.00000
Cumulative Proportion 0.99999 0.99999 0.99999 0.99999 0.99999 0.99999 1.00000
PC141 PC142 PC143 PC144 PC145 PC146
Standard deviation 0.01195 0.01106 0.01042 0.009156 0.008349 0.007473
Proportion of Variance 0.00000 0.00000 0.00000 0.000000 0.000000 0.000000
Cumulative Proportion 1.00000 1.00000 1.00000 1.000000 1.000000 1.000000
PC147 PC148 PC149 PC150 PC151 PC152
Standard deviation 0.006681 0.005886 0.005404 0.004543 0.003973 0.002793
Proportion of Variance 0.000000 0.000000 0.000000 0.000000 0.000000 0.000000
Cumulative Proportion 1.000000 1.000000 1.000000 1.000000 1.000000 1.000000
PC153 PC154 PC155 PC156 PC157 PC158
Standard deviation 0.002337 0.001573 0.0014 0.0009382 0.0006041 0.0002766
Proportion of Variance 0.000000 0.000000 0.0000 0.0000000 0.0000000 0.0000000
Cumulative Proportion 1.000000 1.000000 1.0000 1.0000000 1.0000000 1.0000000
PC159
Standard deviation 0.000000000000004
Proportion of Variance 0.000000000000000
Cumulative Proportion 1.000000000000000В датасет записаны частотности некоторых слов в рассказах А. Чехова и М. Зощенко. Проведите анализ методом главных компонент и визуализируйте первые две компоненты, используя все переменные, и раскрасьте рассказы в зависимости от авторства.
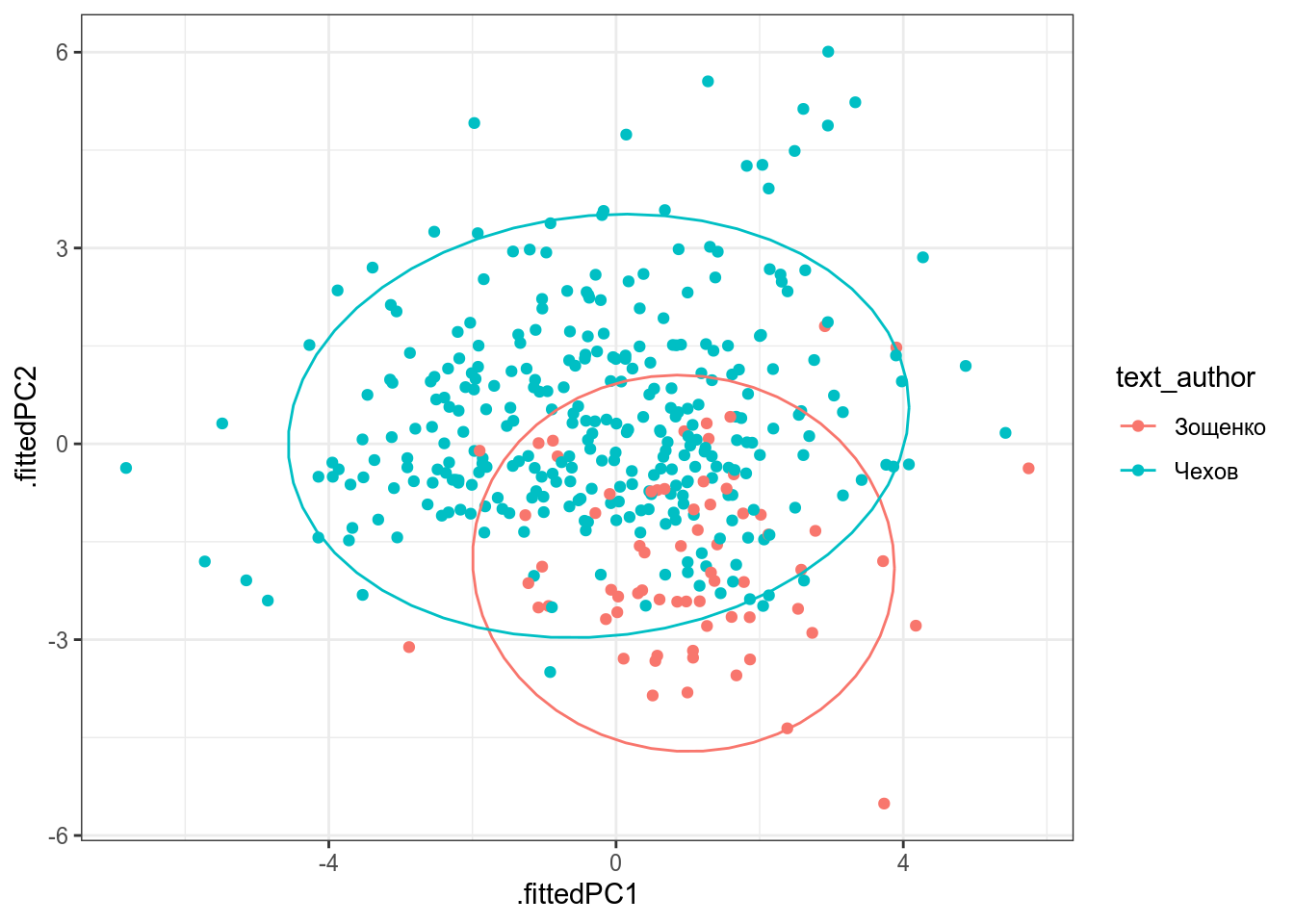
Посчитайте долю кумулятивной дисперсии, объясненной первыми двумя компонентами.
В статье Палитра русской классики Л. Поповец собрала частоту встречаемости цветов в разных произведениях. Проанализируйте датасет методом главных компонент. Обнаружились ли кластеры?
Посчитайте долю кумулятивной дисперсии, объясненной первыми двумя компонентами.
18.5 Другие методы уменьшения размерности
Существуют и другие методы уменьшения размерности:
- CA, MCA
- LDA (Linear Discriminant Analysis), DCA (Discriminant Correspondence Analysis)
- tSNE (t-Distributed Stochastic Neighbor Embedding)
- и другие…