Lab 3. CI

1.1 and 1.2

install.packages("tidyverse")

library(tidyverse)
homo <- read.csv("http://goo.gl/Zjr9aF")
homo %>% 
  group_by(orientation) %>%
  summarise(mean = mean(s.duration.ms),
            CI = 1.96*sd(s.duration.ms)/sqrt(length(s.duration.ms)))

## # A tibble: 2 × 3
##   orientation     mean       CI
##        <fctr>    <dbl>    <dbl>
## 1      hetero 58.46571 5.299922
## 2        homo 63.98286 5.421385

1.3

homo %>% 
  group_by(orientation) %>%
  summarise(mean = mean(s.duration.ms),
            CI = 1.96*sd(s.duration.ms)/sqrt(length(s.duration.ms))) %>% 
  ggplot(aes(orientation, mean))+
  geom_point()+
  geom_errorbar(aes(ymin= mean-CI,
                    ymax = mean+CI), width = 0.3)+
  labs(title = "Mean [s] duration with 95% confidence interval",
       caption = "Data from (Chi-kuk 2007)")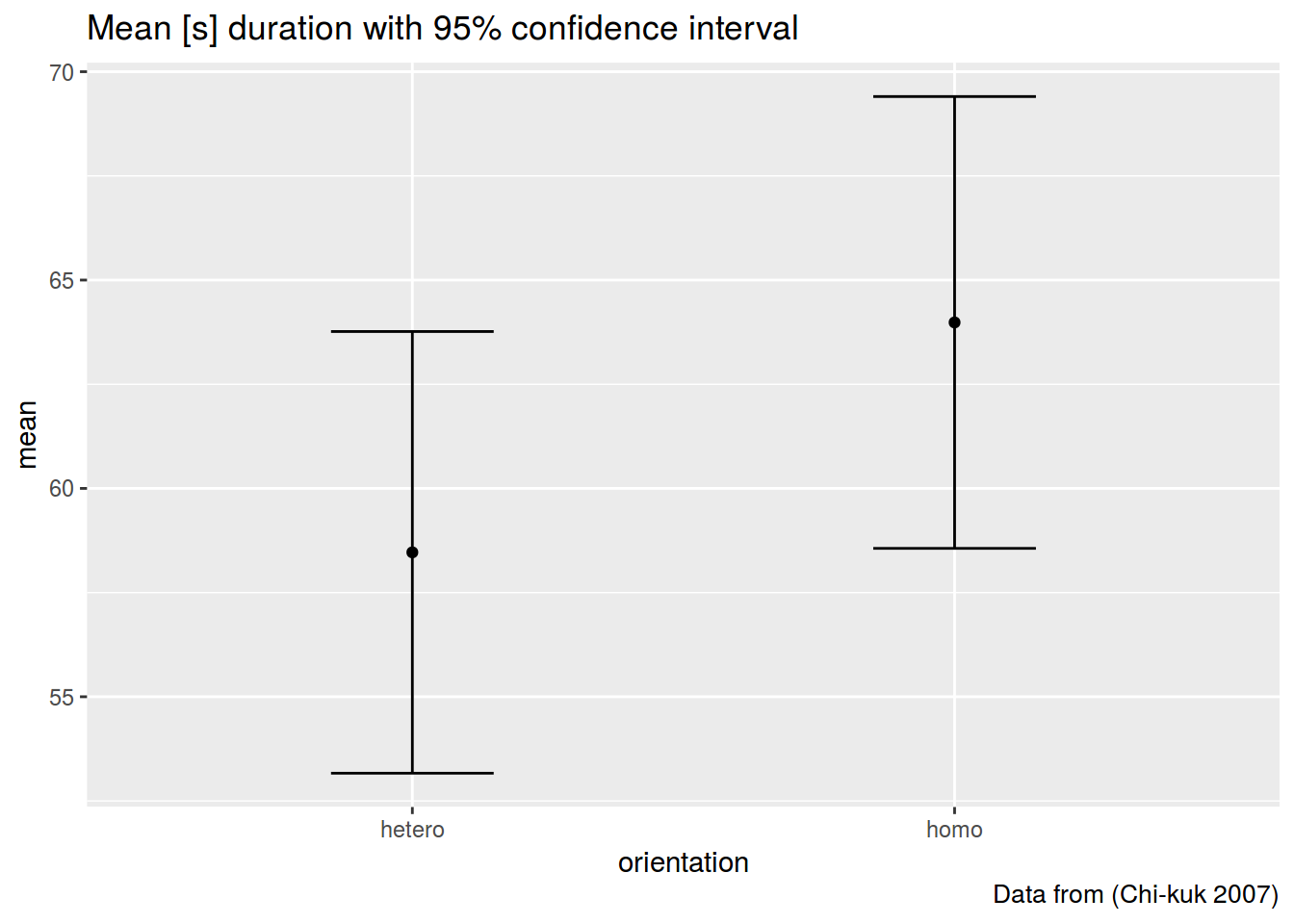

library(tidyverse)
iris %>% 
  ggplot(aes(x = Sepal.Length, y = Sepal.Width, color = Species))+
  geom_point(size = 5)+
  facet_wrap(~Species)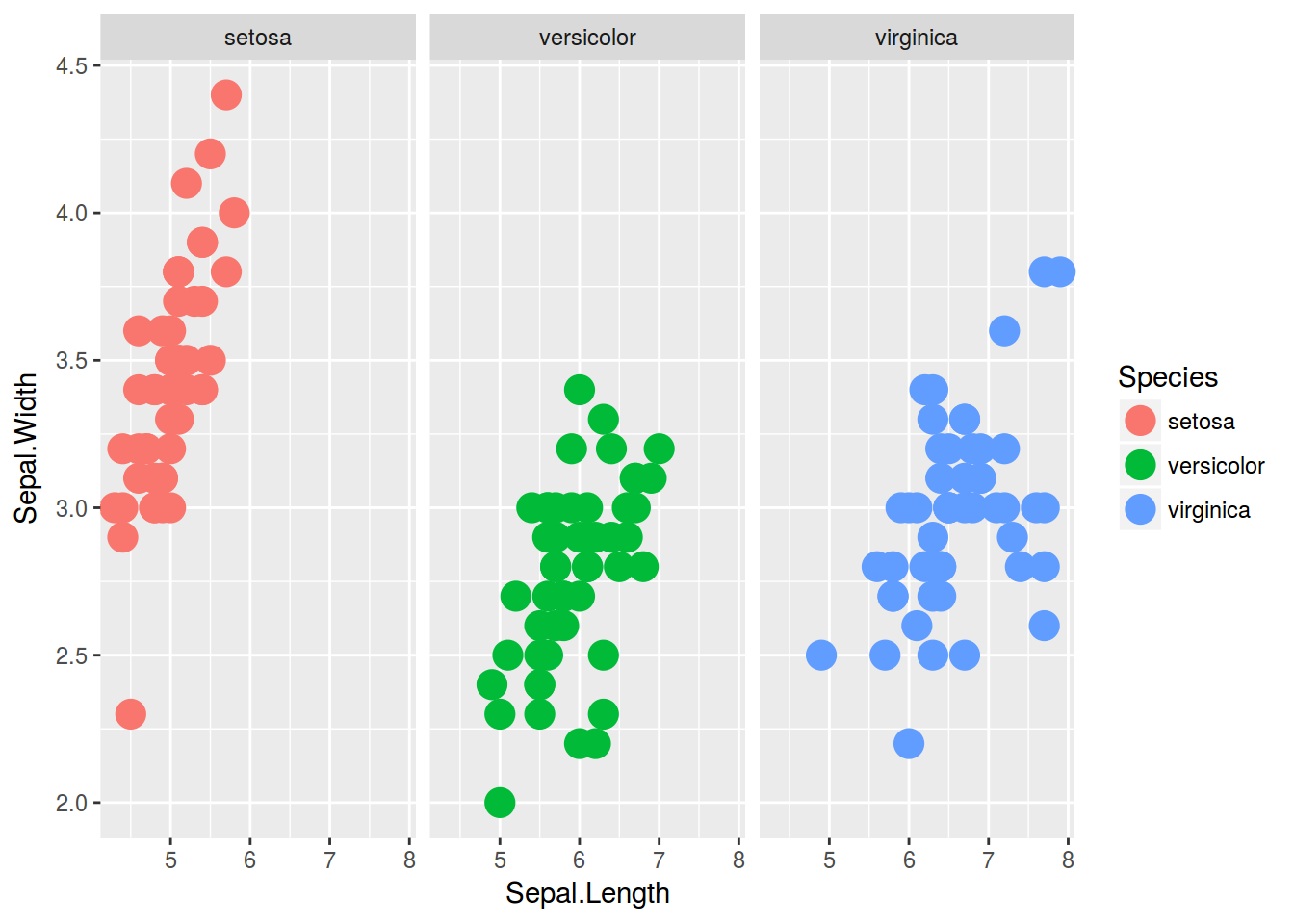

1.4

homo %>% 
  ggplot(aes(s.duration.ms, fill = orientation)) +
  geom_density()+
  geom_rug()+
  facet_wrap(~orientation)+
  labs(title = "[s] duration density plot",
       caption = "Data from (Chi-kuk 2007)")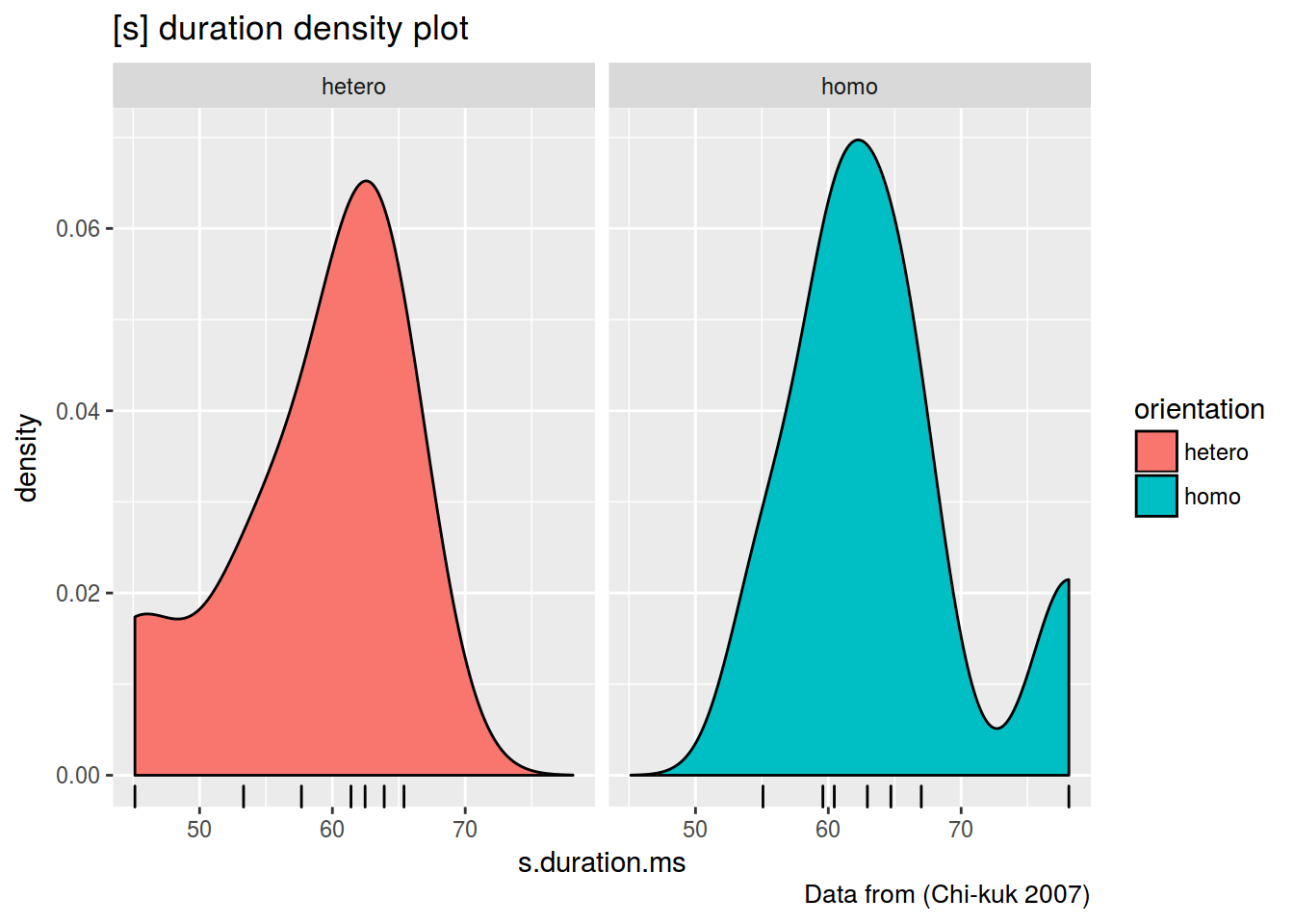

homo %>% 
  ggplot(aes(s.duration.ms, fill = orientation)) +
  geom_density()+
  geom_rug(aes(color = orientation), size = 5)+
  facet_wrap(~orientation)+
  labs(title = "[s] duration density plot",
       caption = "Data from (Chi-kuk 2007)")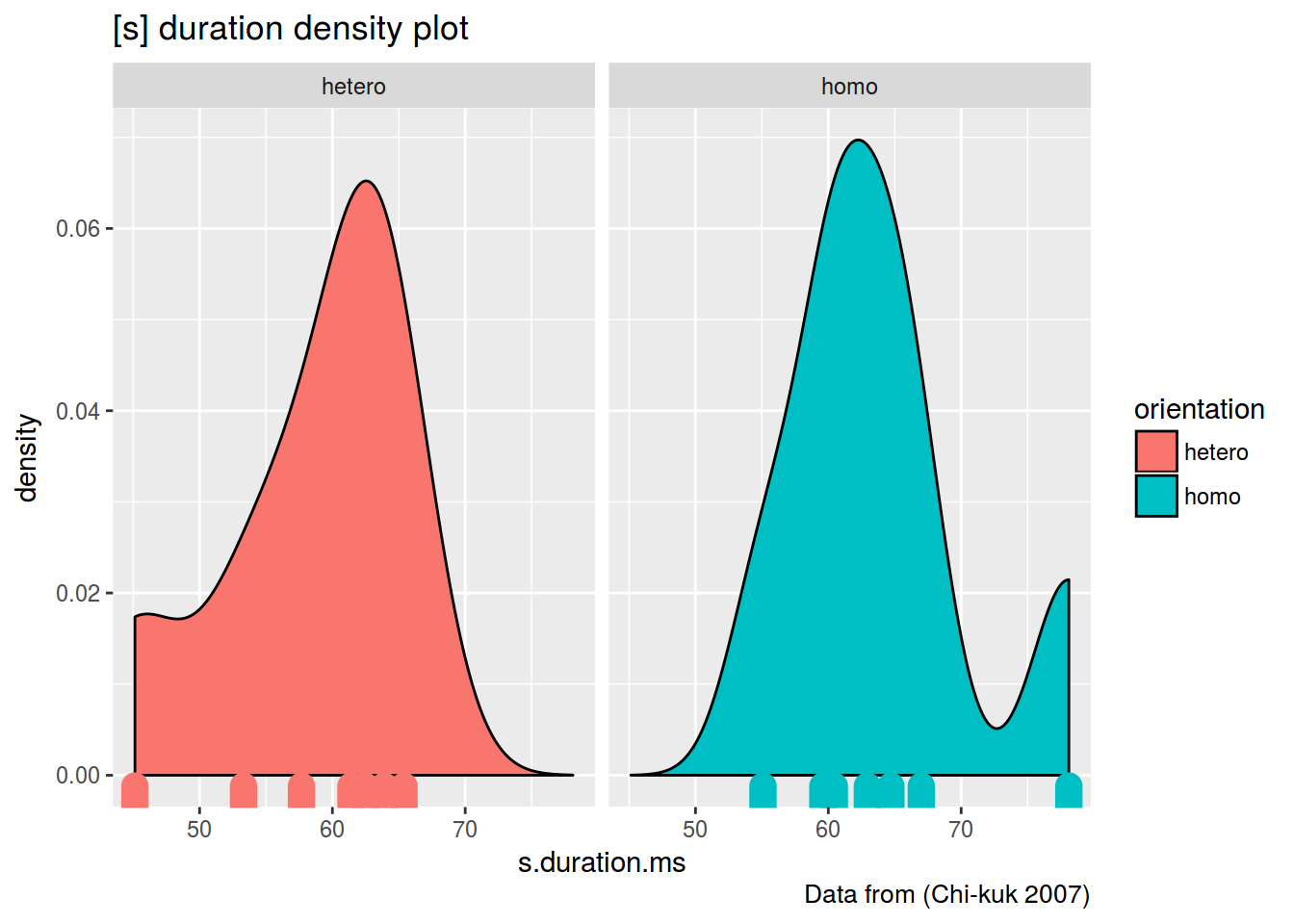

1.5

t.test(s.duration.ms~orientation, data = homo)

## 
##  Welch Two Sample t-test
## 
## data:  s.duration.ms by orientation
## t = -1.4263, df = 11.994, p-value = 0.1793
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  -13.945621   2.911336
## sample estimates:
## mean in group hetero   mean in group homo 
##             58.46571             63.98286

p-value < 0.05…

xkcd: If all else fails, use “significant at p > 0.05 level”; and hope no one notices (it is a joke)

One-sample t-test

df <- read.csv("http://goo.gl/TRRx9Y")
df[df$name == "russian", 2]

##  [1] 267.8670 232.8380 243.4084 225.5630 287.5199 266.7282 292.5137
##  [8] 294.1029 257.6401 232.2932 228.4824 261.8669 246.7714 272.9506
## [15] 220.8743 263.0739 243.9390 284.6122 278.2729 286.2970

t.test(df[df$name == "russian", 2], mu = 240)

## 
##  One Sample t-test
## 
## data:  df[df$name == "russian", 2]
## t = 3.6323, df = 19, p-value = 0.001773
## alternative hypothesis: true mean is not equal to 240
## 95 percent confidence interval:
##  248.2132 270.5483
## sample estimates:
## mean of x 
##  259.3808

Paired t-test

df <- read.csv("http://goo.gl/MNkVws", sep="\t")
t.test(df$LI.Front, df$LI.Temp, paired = TRUE)

## 
##  Paired t-test
## 
## data:  df$LI.Front and df$LI.Temp
## t = 2.8581, df = 11, p-value = 0.01557
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
##  0.07855312 0.60478021
## sample estimates:
## mean of the differences 
##               0.3416667